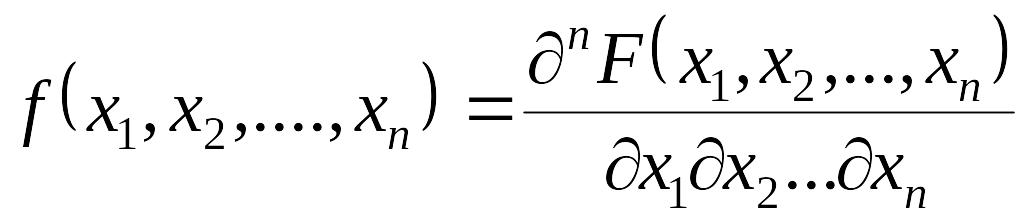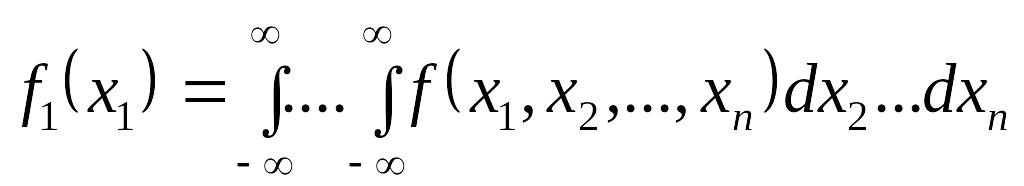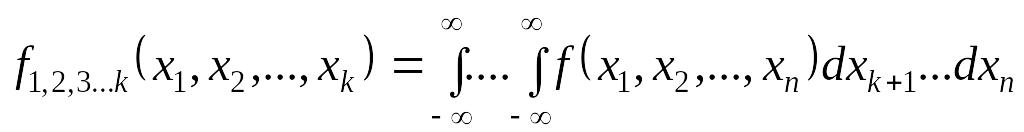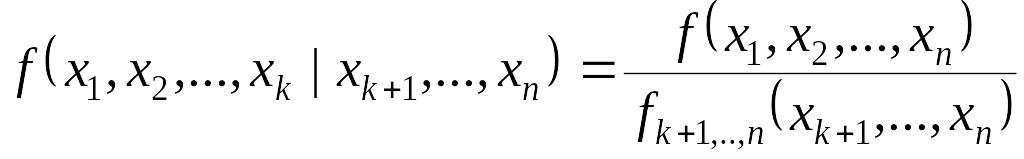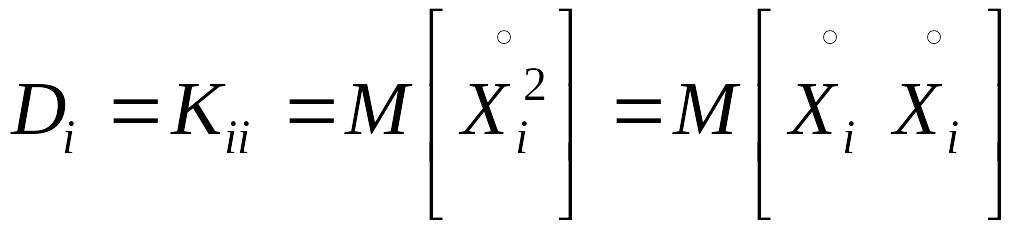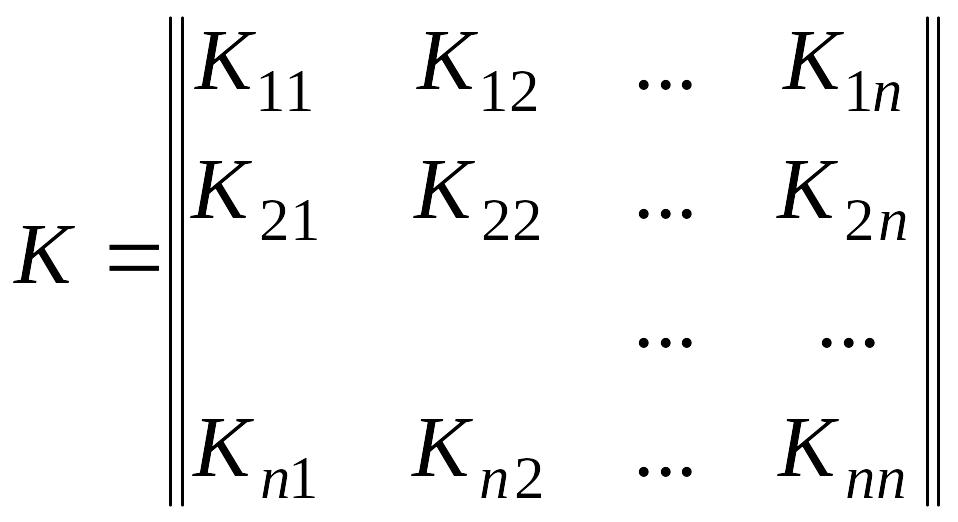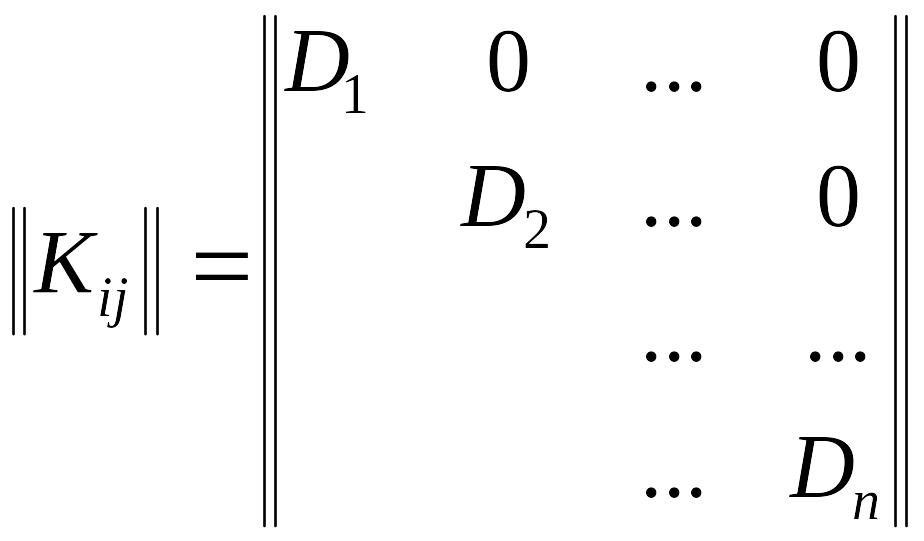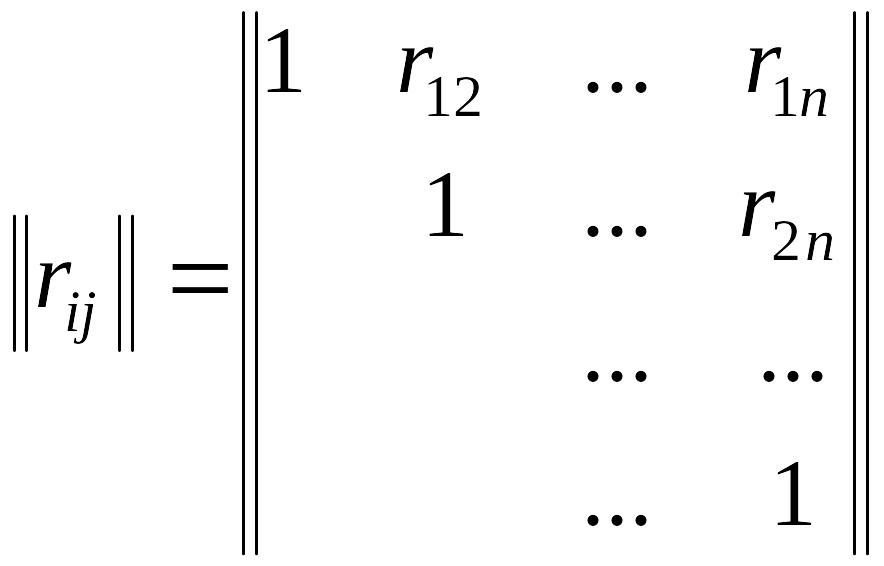- •Раздел 1. Лекции
- •Тема 1. Случайные события
- •Лекция 1
- •Введение
- •Предмет теории вероятностей
- •Основные понятия и определения теории вероятностей
- •Действия над событиями Алгебра событий
- •Свойства событий
- •Частота события
- •Классическое определение вероятности
- •Полная группа событий
- •Геометрическое определение вероятности
- •Аксиоматическое определение вероятности
- •Свойства вероятности. Условная вероятность
- •Условная вероятность.
- •Лекция 2 Основные теоремы теории вероятностей
- •2.1. Теорема сложения вероятностей несовместных событий
- •2.2. Теорема сложения вероятностей совместных событий
- •Лекция 3 Основные формулы вычисления вероятностей сложных событий
- •3.1. Формула полной вероятности
- •3.2. Теорема гипотез. Формула Байеса
- •3.3. Частная теорема о повторении опытов. Теорема я. Бернулли
- •Тема 2. Случайные величины и их распределения Лекция 4 Закон распределения случайной величины
- •Лекция 5 Числовые характеристики случайных величин
- •5.1. Характеристики положения
- •5.2. Характеристики рассеивания и взаимодействия
- •Лекция 6 Основные дискретные и непрерывные распределения Основные дискретные распределения
- •6.1. Биномиальное распределение
- •6.2. Распределение Пуассона
- •Основные непрерывные распределения
- •6.3. Равномерное распределение
- •6.4. Показательное распределение
- •6.5. Нормальное распределение
- •6.6. Распределение "хи-квадрат"
- •6.7. Распределение Стьюдента
- •Тема 3. Случайные векторы. Законы распределения и числовые характеристики Лекция 7 Системы случайных величин (случайные векторы)
- •Функция распределения системы двух случайных величин
- •Числовые характеристики системы двух случайных величин
- •Лекция 8 Система произвольного числа случайных величин
- •Числовые характеристики системы нескольких случайных величин
- •Лекция 9 Законы распределения отдельных компонент, входящих в систему. Условные законы распределения
- •Тема 4. Зависимые и независимые случайные величины Лекция 10
- •Квантиль
- •Тема 7. Случайные последовательности и их сходимость Лекция 14 Виды сходимости последовательностей случайных величин
- •Тема 8. Закон больших чисел. Центральная предельная теорема Лекция 15 предельные теоремы теории вероятностей
- •7.1. Неравенство Чебышева
- •Лекция 16 предельные теоремы теории вероятностей
- •Лекция 17 центральная предельная теорема
- •Тема 9. Первичный статистический анализ результатов измерений случайной величины Лекция 18 Основные понятия математической статистики
- •Статистическое распределение выборки
- •Лекция 19 Полигон частот и гистограмма
- •Эмпирическая функция распределения
- •Тема 10. Точечное оценивание параметров распределений случайных величин Лекция 20 Точечные оценки параметров распределений
- •Оценка математического ожидания случайной величины
- •Оценка дисперсии наблюдаемой случайной величины
- •Оценка вероятности случайного события
- •Лекция 22 Метод наименьших квадратов
- •Метод моментов
- •Тема 11. Интервальное оценивание параметров распределений случайных величин Лекция 23 Построение интервальных оценок параметров распределений
- •Построение доверительного интервала для математического ожидания случайной величины при известной дисперсии
- •Лекция 24 Построение интервальной оценки для математического ожидания и дисперсии Построение доверительного интервала для математического ожидания случайной величины при неизвестной дисперсии
- •Тема 12. Проверка статистических гипотез Лекция 25 Критерий значимости проверки статистических гипотез при принятии решений
- •Критерии согласия Сравнение средних и дисперсии нормальных генеральных совокупностей (малые независимые выборки)
- •Лекция 26 Критерии согласия Сравнение дисперсий по выборкам одинакового объема (критерий Кочрена)
- •Определение типа распределения с помощью критерия Пирсона ("хи-квадрат")
- •Лекция 27 Критерии согласия Критерий согласия Колмогорова
- •Список литературы
Лекция 8 Система произвольного числа случайных величин
Функцией
распределения
системы п
случайных
величин
![]() называется
вероятность совместного выполнения п
неравенств
вида
называется
вероятность совместного выполнения п
неравенств
вида
![]() ,
то есть :
,
то есть :
|
(8. 1) |
Плотностью
распределения
системы п
непрерывных
случайных величин называется n-я
смешанная частная производная функции
![]() ,
взятая один раз по каждому
аргументу:
,
взятая один раз по каждому
аргументу:
|
(8. 2) |
Зная
закон распределения системы, можно
определить законы распределения
отдельных величин, входящих в систему.
Функция
распределения
каждой из величин, входящих в систему,
получится, если в функции распределения
системы положить все остальные аргументы
равными
![]() :
:
|
(8. 3) |
Если
выделить из системы величин
подсистему
![]() ,
то функция распределения этой
подсистемы определяется по формуле
,
то функция распределения этой
подсистемы определяется по формуле
|
(8. 4) |
Плотность распределения каждой из величин, входящих в систему, получится, если плотность распределения системы проинтегрировать в бесконечных пределах по всем остальным аргументам:
|
(8. 5) |
Плотность распределения подсистемы , выделенной из системы , равна:
|
(8. 6) |
Условным
законом распределения подсистемы
называется
ее закон распределения, вычисленный
при условии, что остальные величины
![]() приняли
значения
приняли
значения
![]() .
.
Условная плотность распределения ее может быть вычислена по формуле:
|
(8. 7) |
Случайные
величины
![]() называются
независимыми,
если закон
распределения каждой частной подсистемы,
выделенной из системы
,
не зависит
от того, какие значения приняли остальные
случайные величины.
называются
независимыми,
если закон
распределения каждой частной подсистемы,
выделенной из системы
,
не зависит
от того, какие значения приняли остальные
случайные величины.
Плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему:
|
(8. 8) |
Вероятность попадания случайной точки в пределы n-мерной области D выражается n-кратным интегралом:
|
(8. 9) |
Эта формула по существу является основной формулой для вычисления вероятностей событий, не сводящихся к схеме случаев.
Числовые характеристики системы нескольких случайных величин
Закон распределения системы (заданный функцией распределения или плотностью распределения) является полной, исчерпывающей характеристикой системы нескольких случайных величин. Иногда ограниченность экспериментального материала не дает возможности построить закон распределения системы. В других случаях исследование вопроса с помощью сравнительно громоздкого аппарата законов распределения не оправдывает себя в связи с невысокими требованиями к точности результата.
Во всех таких случаях вместо законов распределения применяют неполное, приближенное описание системы случайных величин с помощью минимального количества числовых характеристик.
Минимальное число характеристик, с помощью которых может быть охарактеризована система п случайных величин , сводится к следующему:
1) вектор математических ожиданий:
|
(8. 10) |
характеризующий средние значения компонент;
Здесь
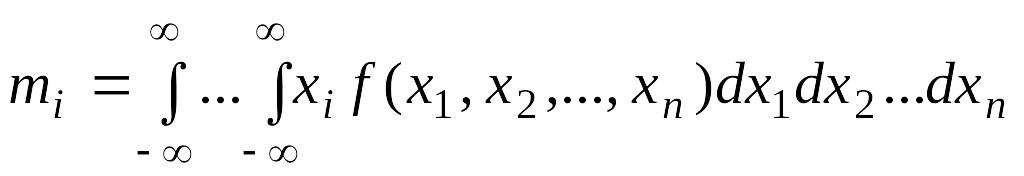
2) вектор дисперсий
|
(8.11) |
характеризующий рассеивание компонент;
Здесь
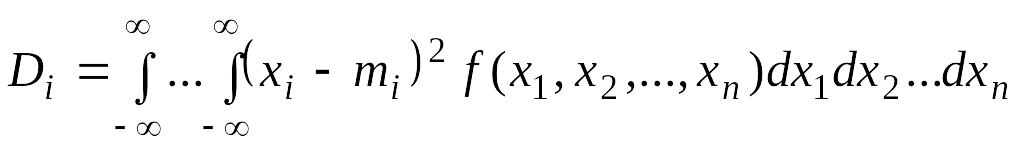
3)
![]() корреляционных
моментов
корреляционных
моментов
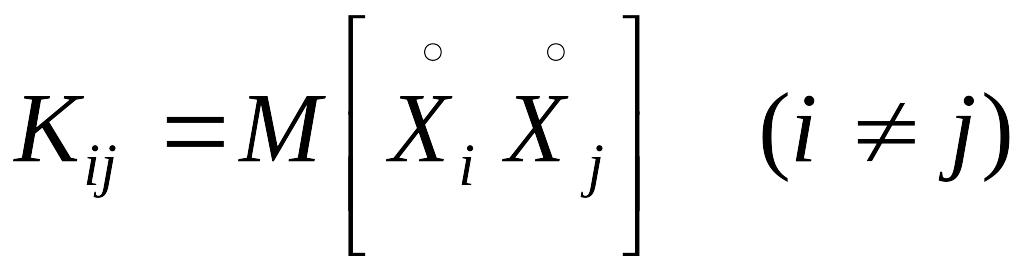
где
![]()
характеризующих попарную корреляцию всех величин, входящих в систему.
Заметим, что дисперсия каждой из случайных величин Хi есть, по существу, не что иное, как частный случай корреляционного момента, а именно:
|
(8.12) |
Все корреляционные моменты и дисперсии удобно расположить в виде прямоугольной таблицы (называемой матрицей):
|
(8.13) |
Эта таблица называется корреляционной матрицей системы случайных величин .
Очевидно,
что не все члены корреляционной матрицы
различны. Из определения корреляционного
момента
ясно, что
![]() ,
т. е. элементы
корреляционной матрицы, расположенные
симметрично по отношению к главной
диагонали, равны.
В связи с этим часто заполняется
не вся корреляционная матрица, а лишь
ее половина, считая от главной диагонали:
,
т. е. элементы
корреляционной матрицы, расположенные
симметрично по отношению к главной
диагонали, равны.
В связи с этим часто заполняется
не вся корреляционная матрица, а лишь
ее половина, считая от главной диагонали:
|
(8.14) |
Корреляционную
матрицу, составленную из элементов
![]() ,
часто
сокращенно обозначают символом
,
часто
сокращенно обозначают символом
![]() .
.
По главной диагонали корреляционной матрицы стоят дисперсии случайных величин .
В случае, когда случайные величины некоррелированны, все элементы корреляционной матрицы, кроме диагональных, равны нулю:
|
|
Такая матрица называется диагональной.
В
целях наглядности суждения именно о
коррелированности случайных величин
пользуются
нормированной
корреляционной матрицей
![]() ,
составленной
не из корреляционных
моментов,
а из коэффициентов
корреляции:
,
составленной
не из корреляционных
моментов,
а из коэффициентов
корреляции:
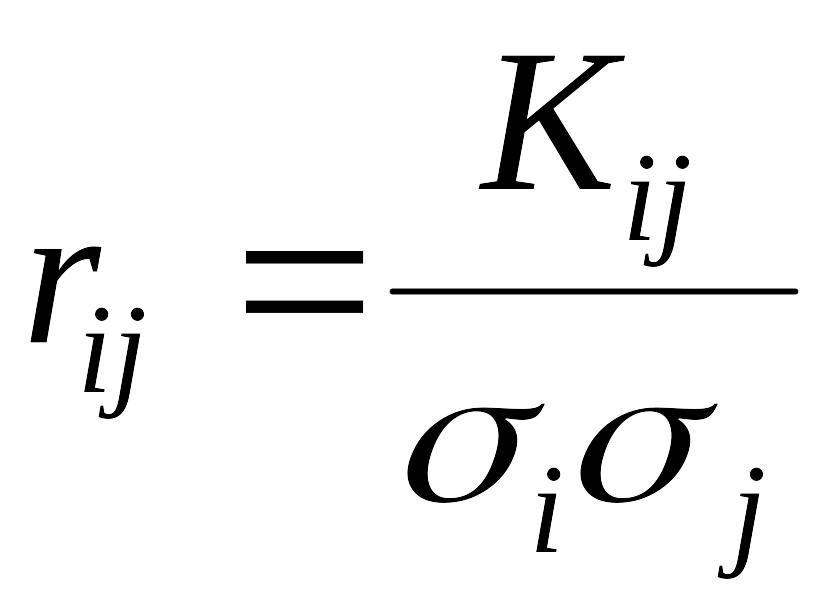 ;
;
![]() .
.
Все диагональные элементы этой матрицы, естественно, равны единице. Нормированная корреляционная матрица имеет вид:
|
(8.15) |
Введем
понятие о некоррелированных системах
случайных величин.
Рассмотрим
две системы случайных величин:
;![]() или два случайных вектора в n-мерном
пространстве: X
с составляющими
и Y
с составляющими
.
или два случайных вектора в n-мерном
пространстве: X
с составляющими
и Y
с составляющими
.
Случайные векторы X и Y называются некоррелированными, если каждая из составляющих вектора X некоррелированная с каждой из составляющих вектора Y:
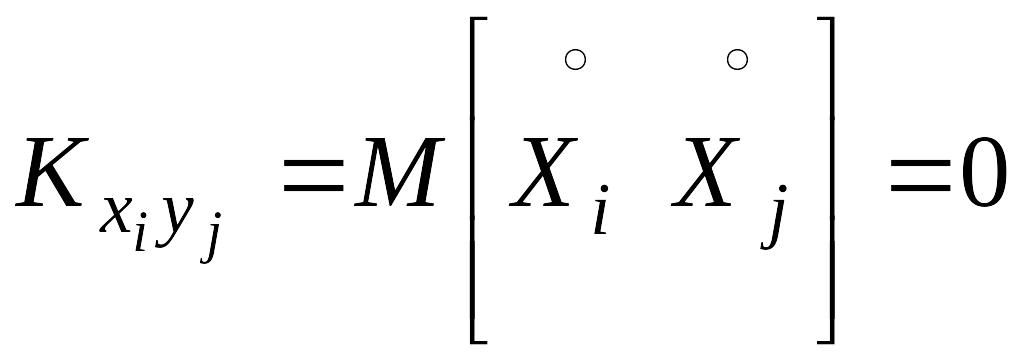
![]()