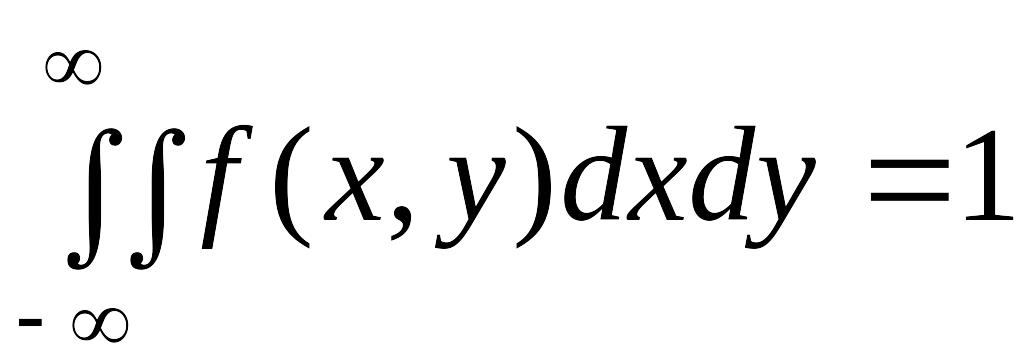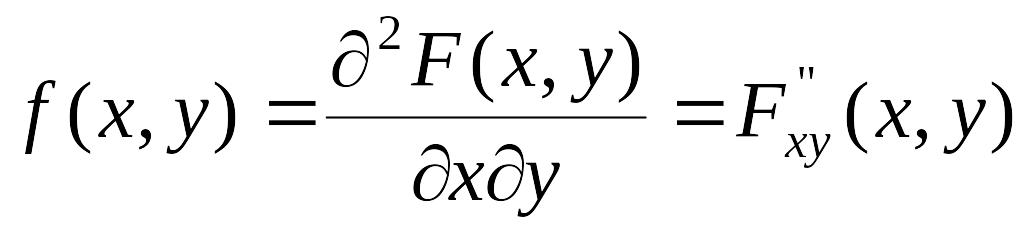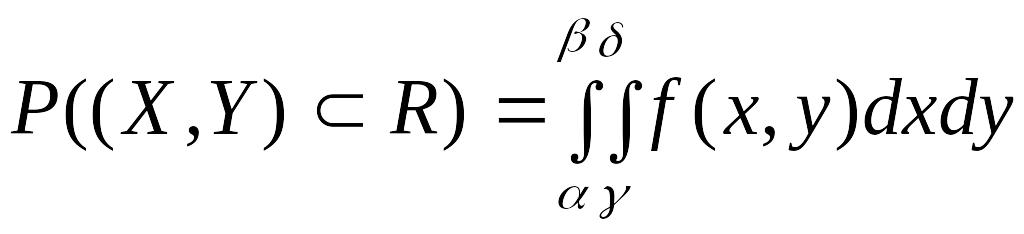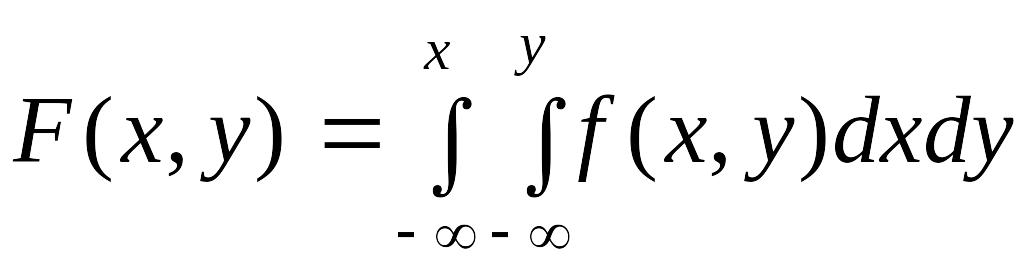Функция распределения системы двух случайных величин

Функцией распределения системы двух случайных величин (X,Y) называется вероятность совместного выполнения двух неравенств X<х и Y<у:

(7.2.1)

Если пользоваться для геометрической интерпретации системы образом случайной точки (случайного вектора), то функция распределения F(х,у) есть не что иное, как вероятность попадания случайной точки (X,Y) в бесконечный квадрант с вершиной в точке (х,у), лежащий левее и ниже ее (рис. 7.2.1).

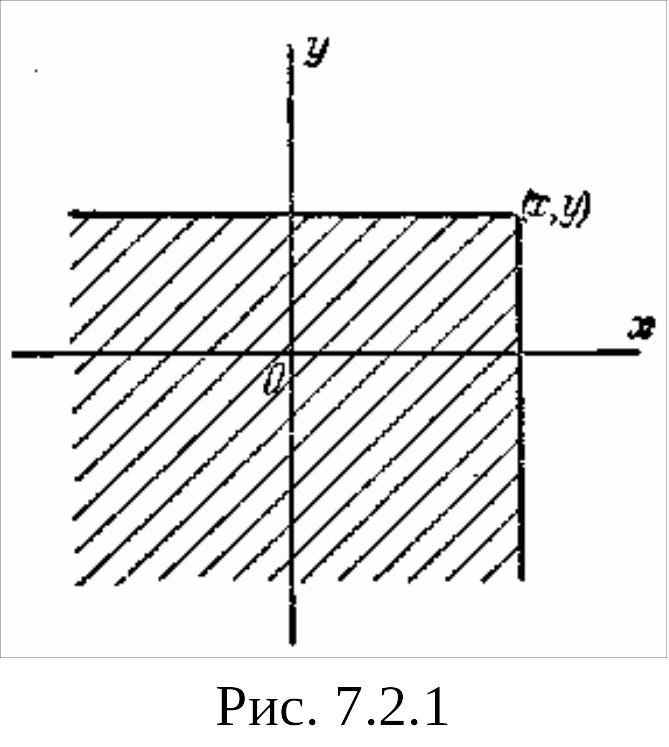
Сформулируем свойства функции распределения системы случайных величин.

1. Функция распределения F(x,у) есть неубывающая функция обоих своих аргументов, т. е.

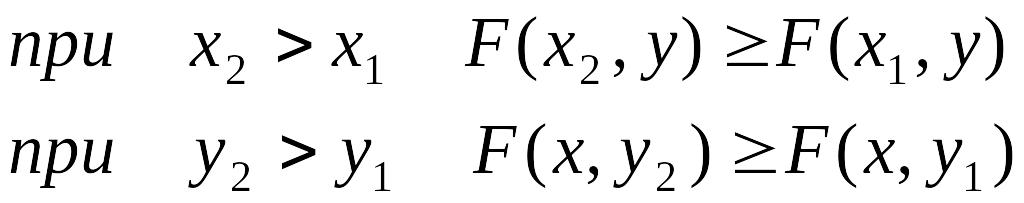
В этом свойстве функции F(х) можно наглядно убедиться, пользуясь геометрической интерпретацией функции распределения как вероятности попадания в квадрант с вершиной (х,у) (рис. 7.2.1). Действительно, увеличивая х (смещая правую границу квадранта вправо) или увеличивая у (смещая верхнюю границу вверх), мы, очевидно, не можем уменьшить вероятность попадания в этот квадрант.

3. Повсюду на функция распределения равна нулю:

F(x, ) = F( , y) = F( , ) = 0.

В этом свойстве мы наглядно убеждаемся, неограниченно отодвигая влево правую границу квадранта (x ) или вниз его верхнюю границу (у ) или делая это одновременно с обеими границами; при этом вероятность попадания в квадрант стремится к нулю.

3. При одном из аргументов, равном , функция распределения системы превращается в маргинальную функцию распределения случайной величины, соответствующей другому аргументу:

F (x, ) = F_l (x), F ( , у) = F₂ (у),

где F₁(x), F₂(y) — соответственно маргинальные функции распределения случайных величин X и Y.

4. Если оба аргумента равны , функция распределения системы равна единице: F( , ) = 1

Действительно, при x , y квадрант с вершиной (х,у) в пределе обращается во всю плоскость хОу, попадание в которую есть достоверное событие.

Условимся событие, состоящее в попадании случайной точки (X, Y) в область D, обозначать символом (X, Y) D.

Вероятность попадания случайной точки в заданную область выражается наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.

Выразим через функцию распределения системы вероятность попадания случайной точки (X, Y) в прямоугольник R, ограниченный абсциссами и ординатами и (рис. 7.2.2).

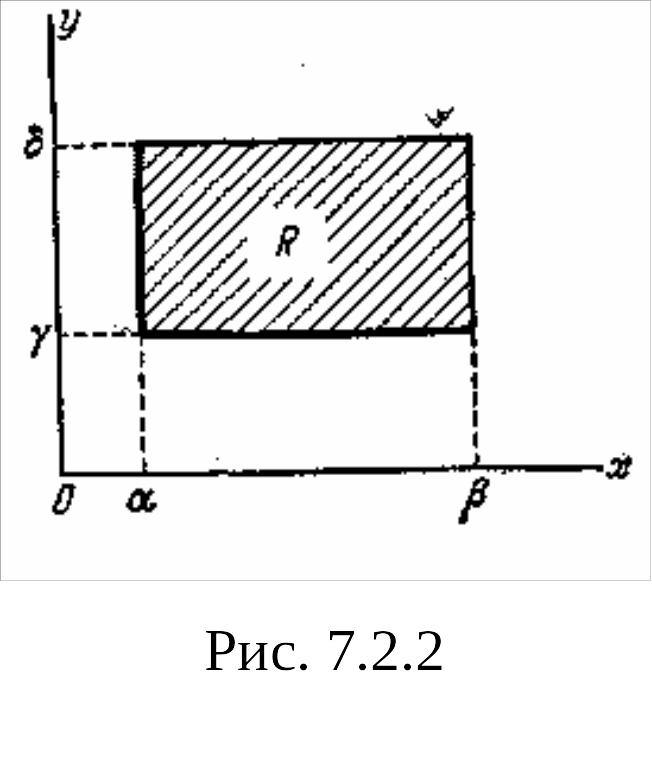
Тогда событие (X,Y) R будет равносильно произведению двух событий: Х и Y . Выразим вероятность этого события через функцию распределения системы. Для этого рассмотрим на плоскости хОу четыре бесконечных квадранта с вершинами в точках рис. 7.2.3.

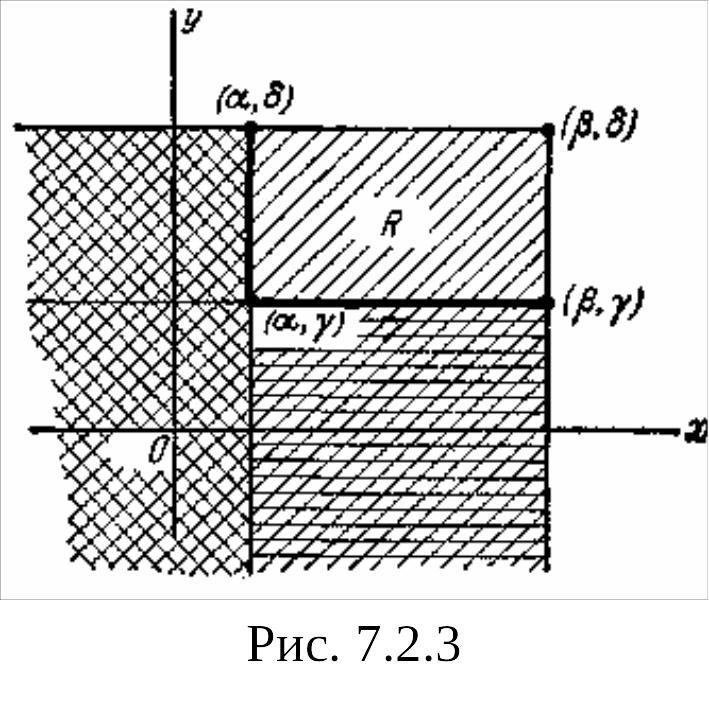
Очевидно, вероятность попадания в прямоугольник R равна вероятности попадания в квадрант минус вероятность попадания в квадрант минус вероятность попадания в квадрант плюс вероятность попадания в квадрант (так как мы дважды вычли вероятность попадания в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:

(7.2.2)

Плотность распределения системы двух случайных величин

Важное практическое значение имеют системы непрерывных случайных величин (непрерывные случайные векторы).

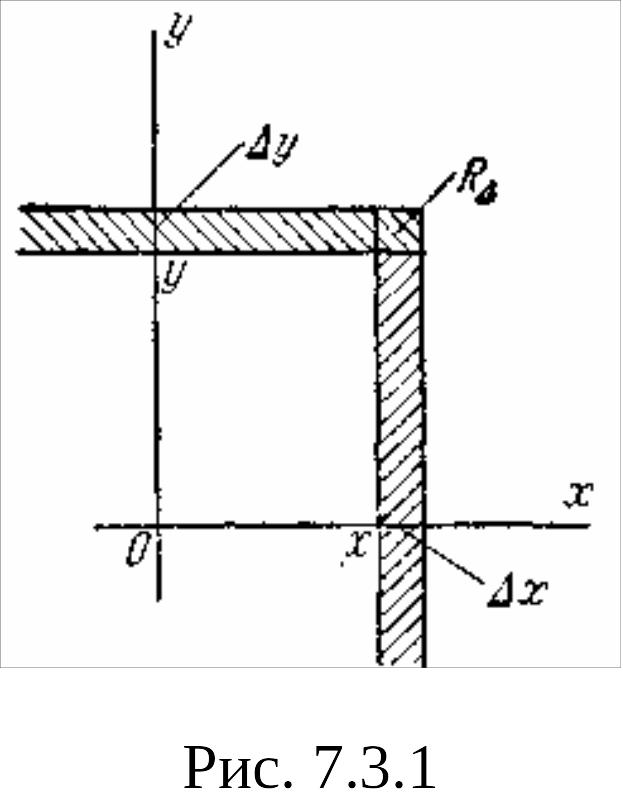
Пусть имеется система двух непрерывных случайных величин (X, Y), которая интерпретируется случайной точкой на плоскости хОу. Рассмотрим на этой плоскости малый прямоугольник со сторонами и , примыкающий к точке с координатами (х,у) (рис. 7.3.1). Вероятность попадания в этот прямоугольник равна

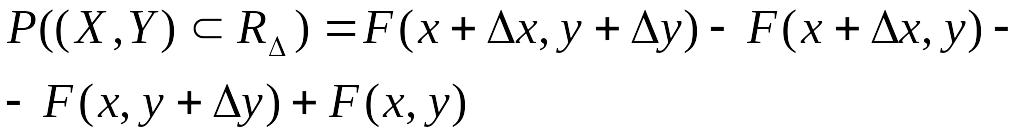
Разделим вероятность попадания в прямоугольник на площадь этого прямоугольника и перейдем к пределу при и :

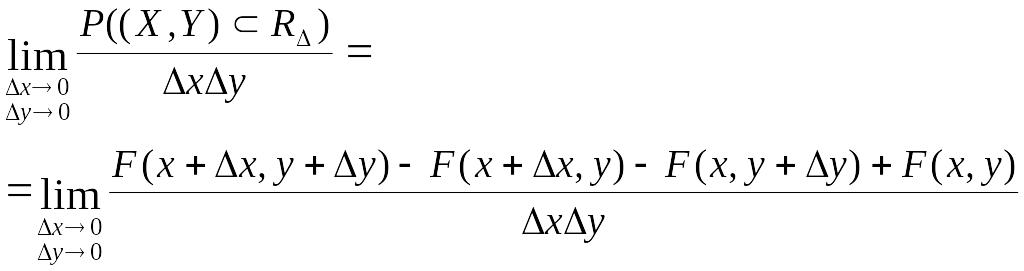
Предположим, что функция F(x, у) не только непрерывна, но и дифференцируема; тогда правая часть формулы представляет собой вторую смешанную частную производную функции F(x, у) по х и у. Обозначим эту производную f(x, у):

(7.3.1)

Функция f(х,у) называется плотностью совместного распределения системы.

Геометрически функцию f(x,у) можно изобразить некоторой поверхностью (рис. 7.3.2). Эта поверхность аналогична кривой распределения для одной случайной величины и называется поверхностью распределения.

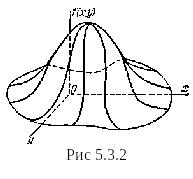
Если пересечь поверхность распределения f(х,у) плоскостью, параллельной плоскости хОу, и спроектировать полученное сечение на плоскость хОу, получится кривая, в каждой точке которой плотность распределения постоянна. Такие кривые называются кривыми равной плотности. Кривые равной плотности, очевидно, представляют собой горизонтали поверхности распределения.

Рассматривая плотность распределения f(х) для одной случайной величины, мы ввели понятие «элемента вероятности» f(x)dx.. Аналогичное понятие «элемента вероятности» вводится и для системы двух случайных величин. Элементом вероятности в данном случае называется выражение

(7.3.2)

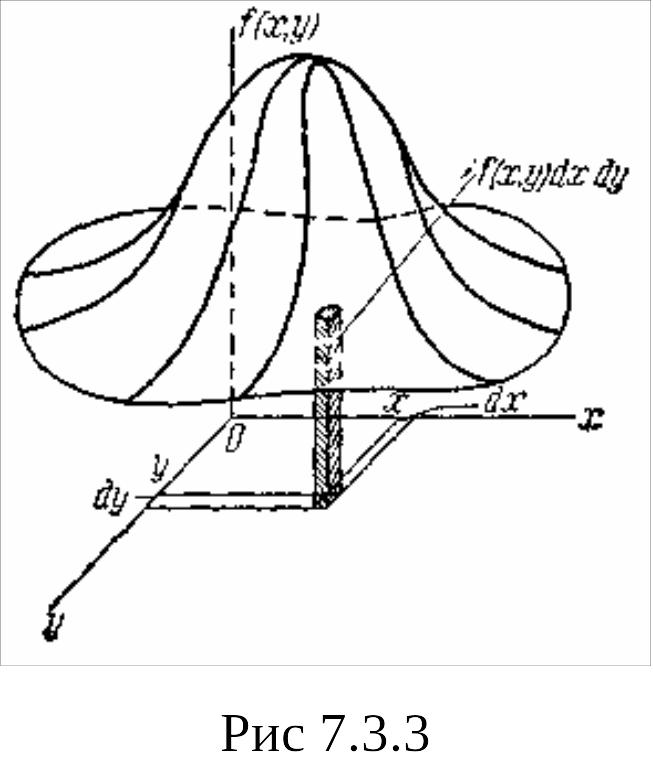
Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами dx,dy, примыкающий к точке (х,у) (рис. 7.3.1). Эта вероятность равна объему элементарного параллелепипеда, ограниченного сверху поверхностью f(x,у) и опирающегося на элементарный прямоугольник dx dy (рис. 7.3.3).

Пользуясь понятием элемента вероятности, выведем выражение для вероятности попадания случайной точки в произвольную область D. Эта вероятность, очевидно, может быть получена суммированием (интегрированием) элементов вероятности по всей области D:

(7.3.3)

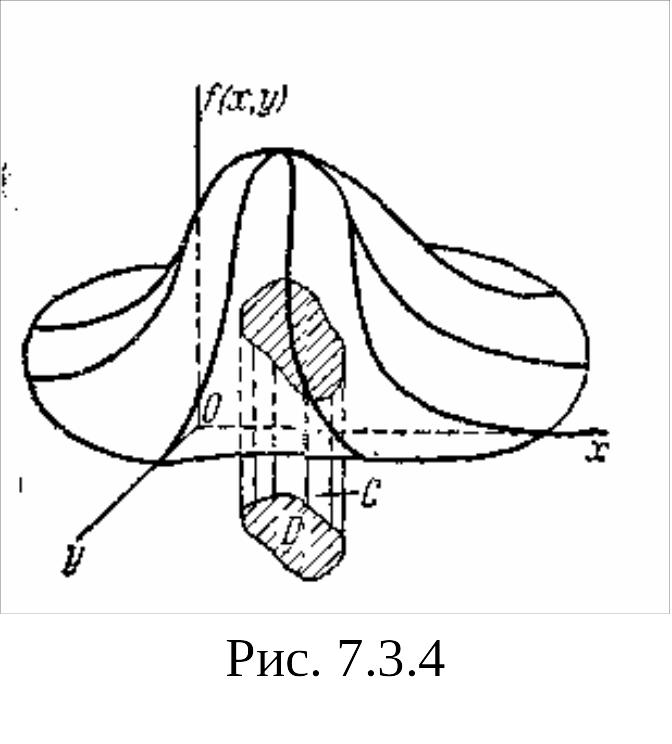
Геометрически вероятность попадания в область D изображается объемом цилиндрического тела С, ограниченного сверху поверхностью распределения и опирающегося на область D (рис. 7.3.4).

Из обшей формулы (7.3.3) вытекает формула для вероятности попадания в прямоугольник R, ограниченный абсциссами и и ординатами и (7.2.2):

Функция распределения F(x,у) есть вероятность попадания в бесконечный квадрант; последний можно рассматривать как прямоугольник, ограниченный абсциссами и х и ординатами и у.

Легко убедиться в следующих свойствах плотности распределения системы:

1. Плотность распределения системы есть функция неотрицательная:

Это ясно из того, что функция распределения является неубывающей функцией своих аргументов.

2. Двойной интеграл в бесконечных пределах от плотности распределения системы равен единице: