
- •Раздел 1. Лекции
- •Тема 1. Случайные события
- •Лекция 1
- •Введение
- •Предмет теории вероятностей
- •Основные понятия и определения теории вероятностей
- •Действия над событиями Алгебра событий
- •Свойства событий
- •Частота события
- •Классическое определение вероятности
- •Полная группа событий
- •Геометрическое определение вероятности
- •Аксиоматическое определение вероятности
- •Свойства вероятности. Условная вероятность
- •Условная вероятность.
- •Лекция 2 Основные теоремы теории вероятностей
- •2.1. Теорема сложения вероятностей несовместных событий
- •2.2. Теорема сложения вероятностей совместных событий
- •Лекция 3 Основные формулы вычисления вероятностей сложных событий
- •3.1. Формула полной вероятности
- •3.2. Теорема гипотез. Формула Байеса
- •3.3. Частная теорема о повторении опытов. Теорема я. Бернулли
- •Тема 2. Случайные величины и их распределения Лекция 4 Закон распределения случайной величины
- •Лекция 5 Числовые характеристики случайных величин
- •5.1. Характеристики положения
- •5.2. Характеристики рассеивания и взаимодействия
- •Лекция 6 Основные дискретные и непрерывные распределения Основные дискретные распределения
- •6.1. Биномиальное распределение
- •6.2. Распределение Пуассона
- •Основные непрерывные распределения
- •6.3. Равномерное распределение
- •6.4. Показательное распределение
- •6.5. Нормальное распределение
- •6.6. Распределение "хи-квадрат"
- •6.7. Распределение Стьюдента
- •Тема 3. Случайные векторы. Законы распределения и числовые характеристики Лекция 7 Системы случайных величин (случайные векторы)
- •Функция распределения системы двух случайных величин
- •Числовые характеристики системы двух случайных величин
- •Лекция 8 Система произвольного числа случайных величин
- •Числовые характеристики системы нескольких случайных величин
- •Лекция 9 Законы распределения отдельных компонент, входящих в систему. Условные законы распределения
- •Тема 4. Зависимые и независимые случайные величины Лекция 10
- •Квантиль
- •Тема 7. Случайные последовательности и их сходимость Лекция 14 Виды сходимости последовательностей случайных величин
- •Тема 8. Закон больших чисел. Центральная предельная теорема Лекция 15 предельные теоремы теории вероятностей
- •7.1. Неравенство Чебышева
- •Лекция 16 предельные теоремы теории вероятностей
- •Лекция 17 центральная предельная теорема
- •Тема 9. Первичный статистический анализ результатов измерений случайной величины Лекция 18 Основные понятия математической статистики
- •Статистическое распределение выборки
- •Лекция 19 Полигон частот и гистограмма
- •Эмпирическая функция распределения
- •Тема 10. Точечное оценивание параметров распределений случайных величин Лекция 20 Точечные оценки параметров распределений
- •Оценка математического ожидания случайной величины
- •Оценка дисперсии наблюдаемой случайной величины
- •Оценка вероятности случайного события
- •Лекция 22 Метод наименьших квадратов
- •Метод моментов
- •Тема 11. Интервальное оценивание параметров распределений случайных величин Лекция 23 Построение интервальных оценок параметров распределений
- •Построение доверительного интервала для математического ожидания случайной величины при известной дисперсии
- •Лекция 24 Построение интервальной оценки для математического ожидания и дисперсии Построение доверительного интервала для математического ожидания случайной величины при неизвестной дисперсии
- •Тема 12. Проверка статистических гипотез Лекция 25 Критерий значимости проверки статистических гипотез при принятии решений
- •Критерии согласия Сравнение средних и дисперсии нормальных генеральных совокупностей (малые независимые выборки)
- •Лекция 26 Критерии согласия Сравнение дисперсий по выборкам одинакового объема (критерий Кочрена)
- •Определение типа распределения с помощью критерия Пирсона ("хи-квадрат")
- •Лекция 27 Критерии согласия Критерий согласия Колмогорова
- •Список литературы
6.6. Распределение "хи-квадрат"
Пусть
![]() (i
= 1,...,n)
– система независимых нормированных
нормально распределенных случайных
величин с математическим ожиданием,
равным нулю, и единичной дисперсией.
(i
= 1,...,n)
– система независимых нормированных
нормально распределенных случайных
величин с математическим ожиданием,
равным нулю, и единичной дисперсией.
Тогда
случайная величина χ![]() ,
представляющая собой сумму квадратов
этих величин, χ
=
,
представляющая собой сумму квадратов
этих величин, χ
=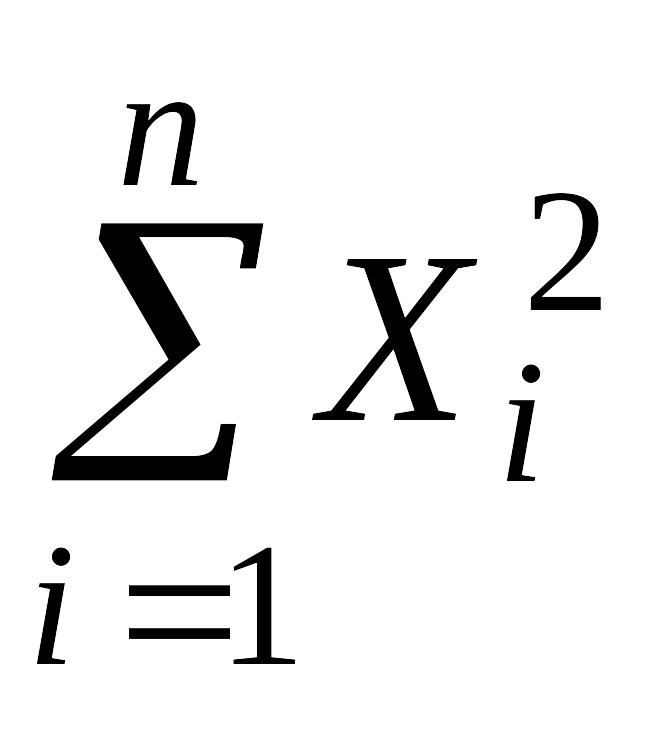 распределена
по закону «хи-квадрат» с k
= n
степенями свободы. Если на величины
(i
= 1,...,n)
наложено r
связей, то число степеней свободы k
= n – r.
распределена
по закону «хи-квадрат» с k
= n
степенями свободы. Если на величины
(i
= 1,...,n)
наложено r
связей, то число степеней свободы k
= n – r.
Плотность этого распределения определяется выражением
p (χ
)
(χ
)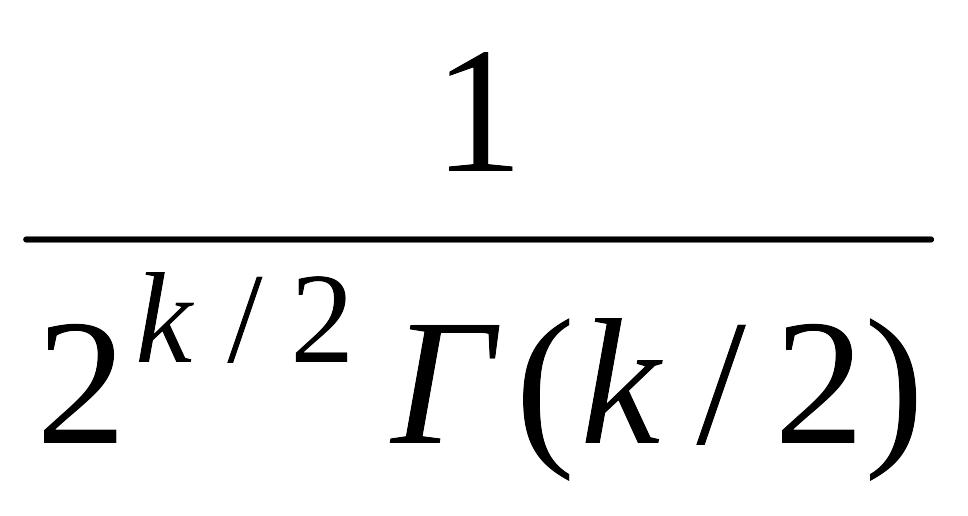 (χ
)
(χ
)![]() exp(–χ
/2), 0
≤ χ
<
∞ ,
exp(–χ
/2), 0
≤ χ
<
∞ ,
где
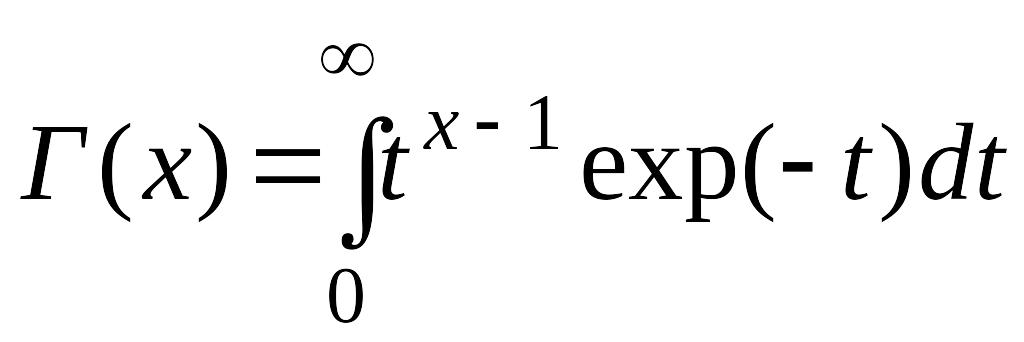 –
гамма-функция
(интеграл Эйлера второго рода). В
частности, Г(n
+1) = n!
.
–
гамма-функция
(интеграл Эйлера второго рода). В
частности, Г(n
+1) = n!
.
Из определения плотности вероятности распределения χ следует, что распределение «хи-квадрат» определяется одним параметром: числом степеней свободы k.
С увеличением числа степеней свободы распределение «хи-квадрат» медленно приближается к нормальному. При k = n > 30 χ –распределение достаточно хорошо представляется нормальным законом с M[χ ] = n и D[χ ] = n. На (рис.6.12) показано, как изменяется характер распределения «хи-квадрат» при увеличении числа степеней свободы k.
6.7. Распределение Стьюдента
Пусть
случайные величины Z,
![]() подчинены нор-мальному закону распределения
с нулевым средним и произвольной
дисперсией. Пусть далее величина Z
не зависит от
,
и среди
имеется ровно k
линейно
независимых величин. Тогда случайная
величина
подчинены нор-мальному закону распределения
с нулевым средним и произвольной
дисперсией. Пусть далее величина Z
не зависит от
,
и среди
имеется ровно k
линейно
независимых величин. Тогда случайная
величина
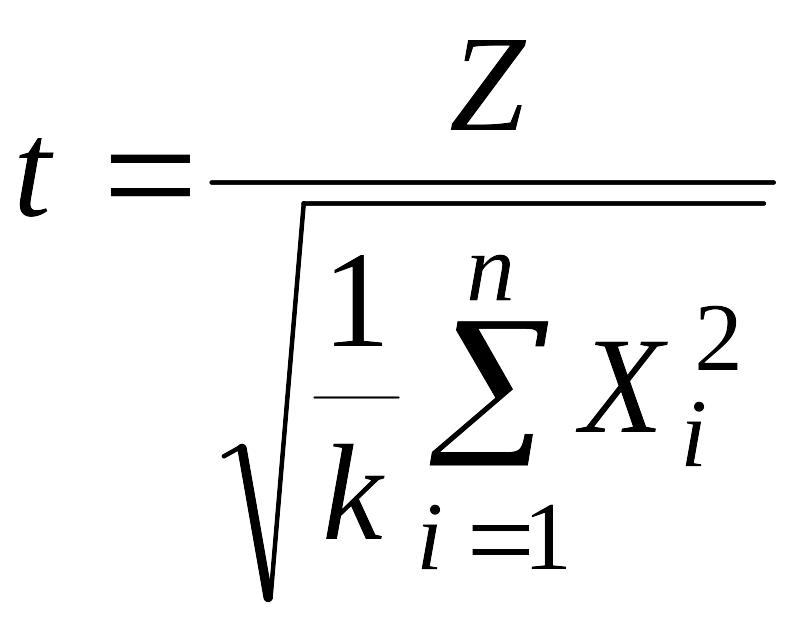

имеет распределение Стьюдента
(t-распределение) (рис.6.13) с функ-цией плотности распределения
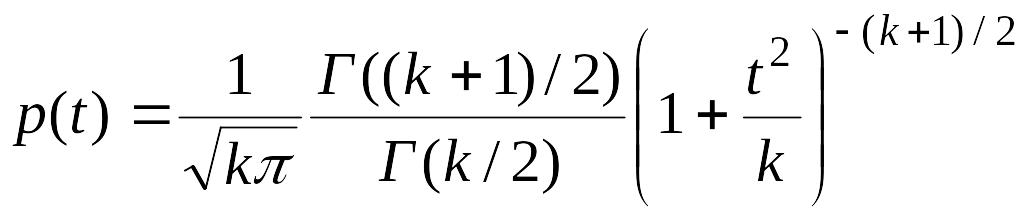 .
.
Заметим, что t-распределение не зависит от . Величина t, определенная для нормированных случайных величин с нулевым средним и единичной дисперсией также распределена по закону Стьюдента.
Распределение Стьюдента симметрично относительно начала координат. С возрастанием числа степеней свободы быстро приближается к нормальному распределению. Для нормированных случайных величин распределение Стьюдента приближается к нормальному закону с характеристиками:
M[t
] = 0 и D[t
] =
![]() .
.
6.8. F-распределение Фишера
Е сли
X
и Y
– независимые случайные величины,
распределенные по закону «хи-квадрат»
со степенями свободы
сли
X
и Y
– независимые случайные величины,
распределенные по закону «хи-квадрат»
со степенями свободы
![]() и
и
![]() ,
то величина
,
то величина
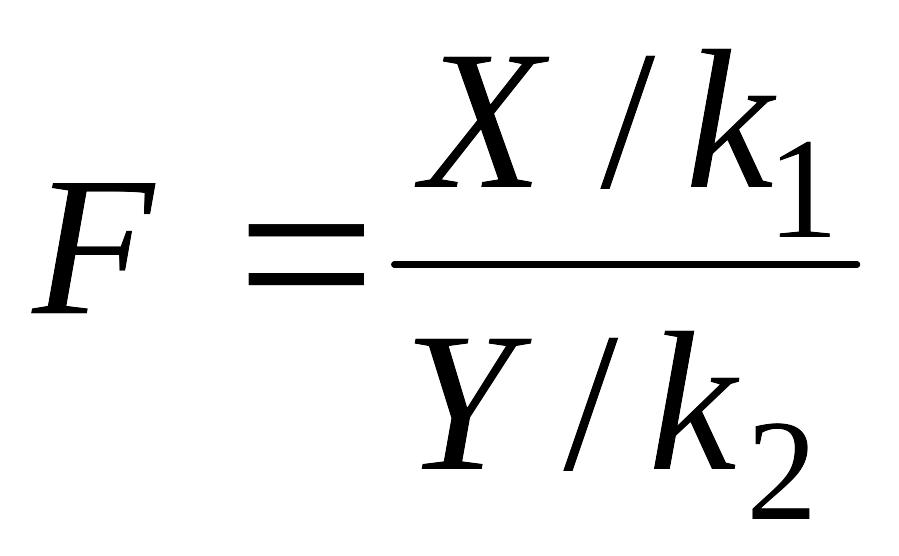
имеет F-распределение Фишера со степенями свободы и . Плотность этого распределения (рис.6.14) определяется выражением
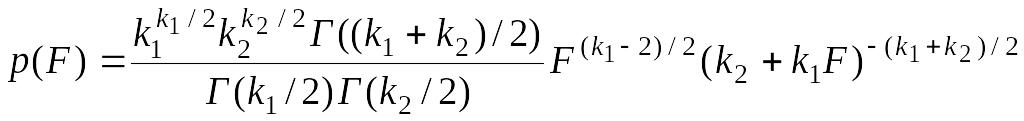 .
.
Таким образом, F-распределение Фишера характеризуется двумя параметрами – числами степеней свободы и .
Тема 3. Случайные векторы. Законы распределения и числовые характеристики Лекция 7 Системы случайных величин (случайные векторы)
Понятие о системе случайных величин
В практических приложениях теории вероятностей очень часто приходится сталкиваться с задачами, в которых результат опыта описывается двумя или более случайными величинами, образующими систему или вектор. Например, при стрельбе группой из п выстрелов совокупность точек попадания на плоскости может рассматриваться как система 2n случайных величин: п абсцисс и п ординат точек попадания. Условимся систему нескольких случайных величин называть случайным вектором и обозначать Х= (X1, Х2,...., Хn).
Свойства системы случайных величин (или случайного вектора) не исчерпываются свойствами отдельных компонент: помимо этого, они включают также взаимные связи (зависимости) между случайными компонентами.
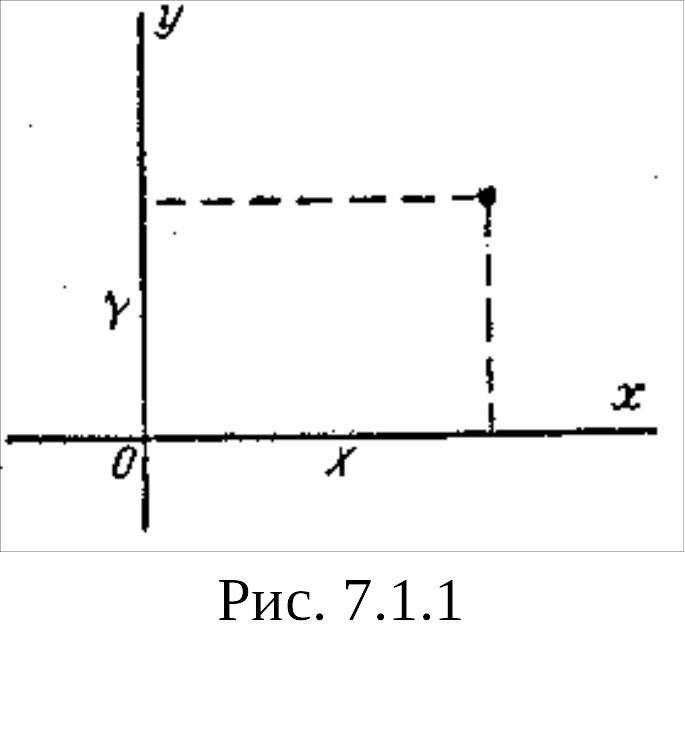
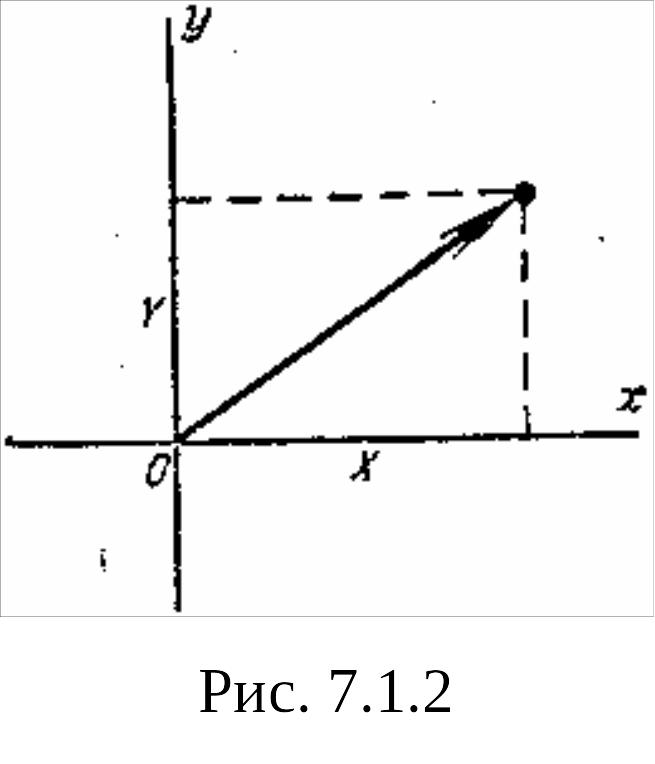
При рассмотрении вопросов, связанных с системами случайных величин, удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин (X,Y) можно изображать случайной точкой на плоскости с координатами X и Y (рис. 7.1.1). Аналогично система трех случайных величин может быть изображена случайной точкой в трехмерном пространстве. Часто бывает удобно говорить о системе п случайных величин как о «случайной точке в пространстве п измерений». Вместо образа случайной точки для геометрической интерпретации системы случайных величин пользуются образом случайного вектора. Систему двух случайных величин при этом рассматривают как случайный вектор на плоскости хОу, составляющие которого по осям представляют собой случайные величины X, Y (рис. 7.1.2).
При этом теория систем случайных величин рассматривается как теория случайных векторов.
В данном курсе мы будем в зависимости от удобства изложения пользоваться как одной, так и другой интерпретацией.
Занимаясь изучением свойств случайных векторов, мы будем рассматривать как полные, исчерпывающие вероятностные характеристики — законы распределения, так и неполные — числовые характеристики.
Изложение начнем с наиболее простого случая системы двух случайных величин(двухмерного случайного вектора).
