5.2. Характеристики рассеивания и взаимодействия

Основными характеристиками рассеивания случайной величины являются моменты.

На практике используются в основном моменты двух видов: начальные и центральные.

Начальным моментом k-го порядка случайной величины X называется математическое ожидание k-й степени от этой случайной величины, т.е. .

Для дискретной случайной величины:

= .

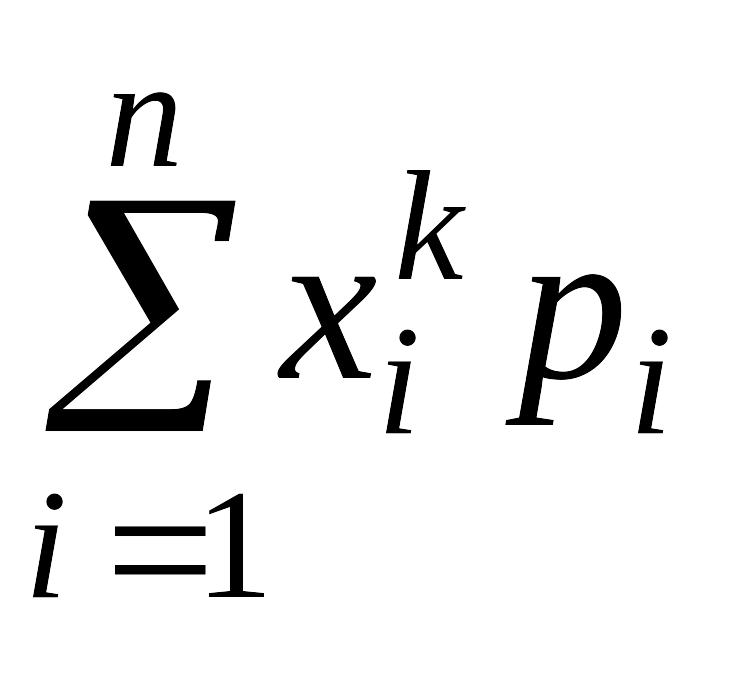Для непрерывной случайной величины:

= .

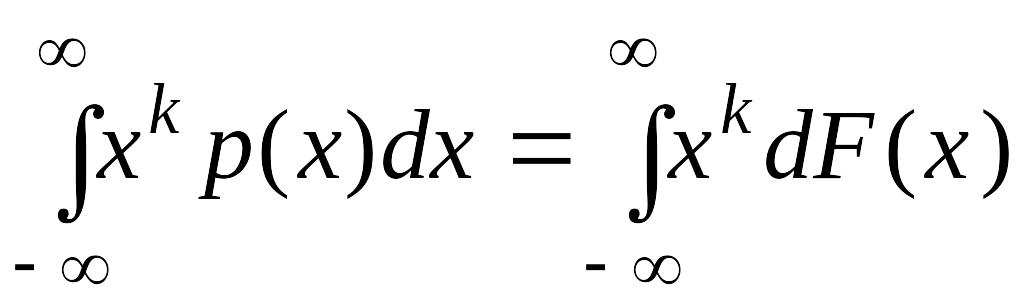Нетрудно видеть, что момент первого порядка совпадает с математическим ожиданием случайной величины.

Для определения центрального момента дадим определение

центрированной случайной величины .

Центрированной случайной величиной , соответствующей случайной величине X, называется отклонение случайной величины от ее математического ожидания M[X] = m, т.е. = X – m.

Математическое ожидание центрированной случайной величины равно нулю M[ ] = 0.

Действительно для дискретной случайной величины X

M[ ] = M[X – m] = .

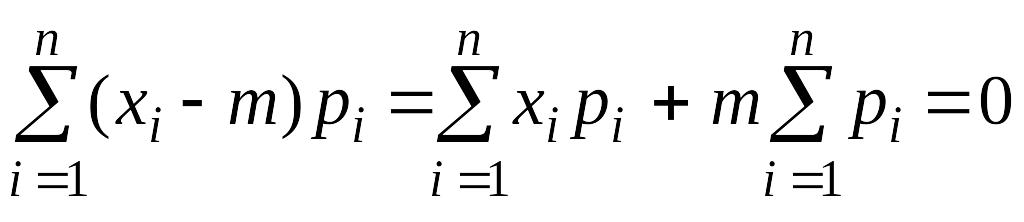Аналогичное имеет место для непрерывных случайных величин.

Начало координат совпадает с M[ ] = 0. Поэтому переход к центрированным случайным величинам , равносилен переносу начала координат в точку, равную m .

Центральным моментом k-го порядка случайной величины X называется математическое ожидание k-ой степени центрированной случайной величины , т.е. .

Для дискретной случайной величины X:

= .

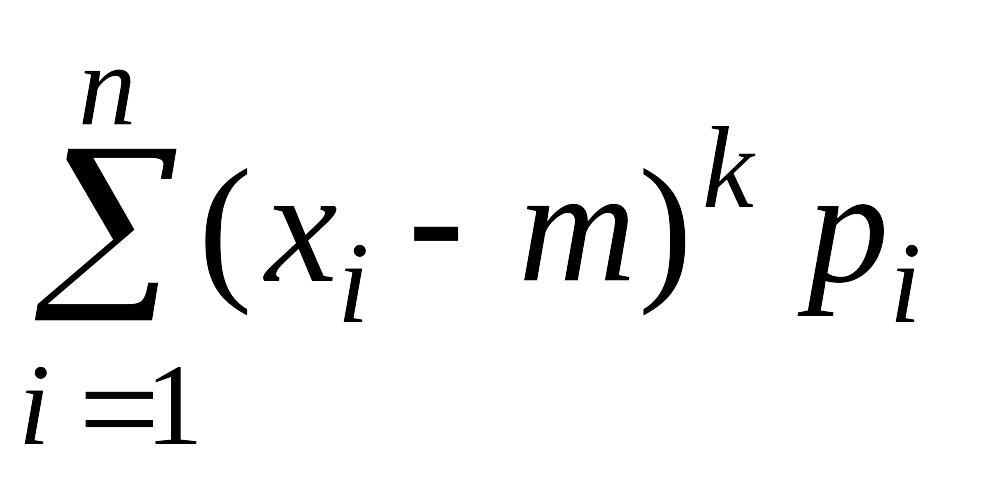Для непрерывной случайной величины X:

= .

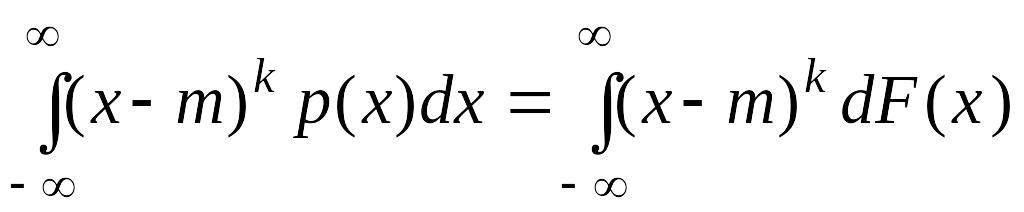Нетрудно видеть, что центральный момент первого порядка – первый центральный момент равен нулю: = M[ ] = M[X – m] = 0.

Центральный и начальный момент первого и второго порядка связаны между собой выражением:

= M[ ] = M[ ] = =

= .

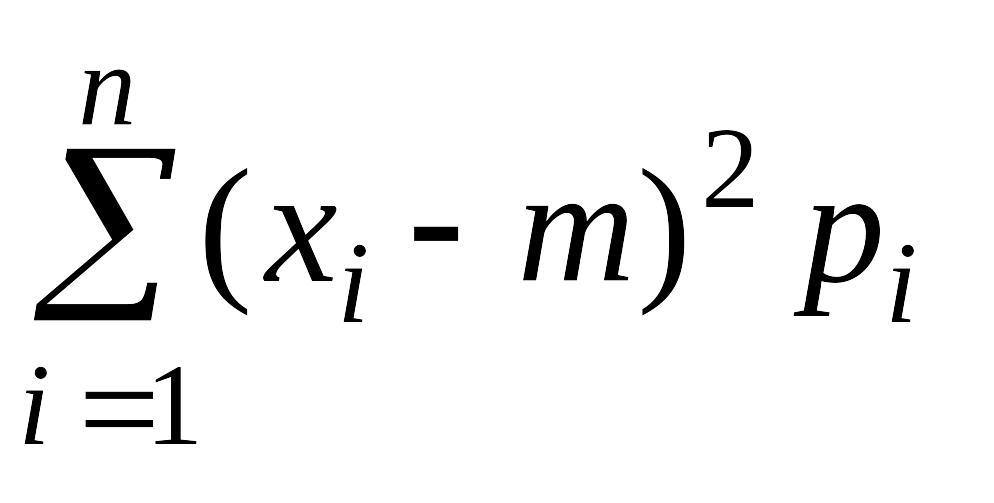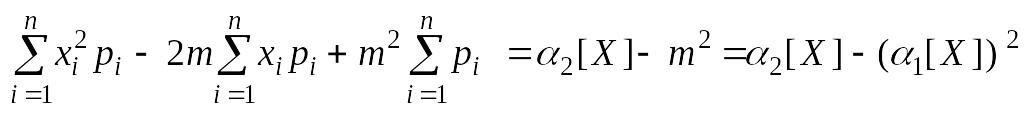Второй центральный момент называется дисперсией случайной величины, которая характеризует рассеивание значений случайной величины.

Ввиду исключительной важности этой характеристики среди других моментов для нее вводится специальное обозначение.

.

Дисперсией случайной величины называется математическое ожидание квадрата соответствующей центрированной случайной величины.

Для дискретной случайной величины:

= M[ ] = M[ ] = .

Для непрерывной случайной величины

= .

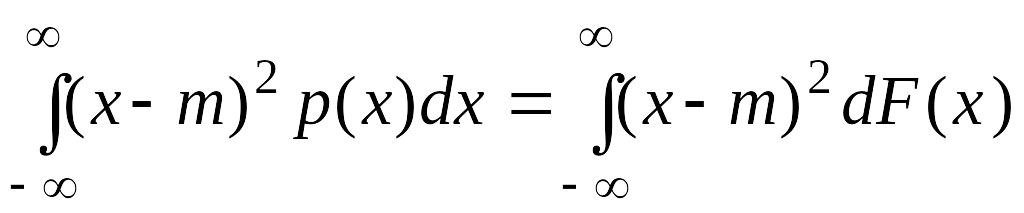Д исперсия случайной величины имеет размерность квадрата случайной величины, поэтому для наглядной характеристики рассеивания, размерность которой совпадает с размерностью случайной величины, используют среднее квадратическое, или стандартное отклонение случайной величины σ: σ = .

Для оценки степени независимости случайной величины X и Y вводится числовая характеристика, называемая корреляционным (ковариационным) моментом случайных величин X и Y.

Корреляционным (ковариационным) моментом случайных величин X и Y называют число K(x,y) = M{(X– M[X])(Y – M[Y])} = M[XY] – M[X]M[Y]. Для дискретных случайных величин:

.

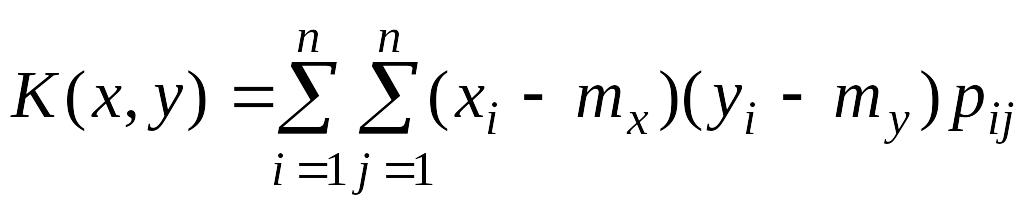Для непрерывных случайных величин:

.

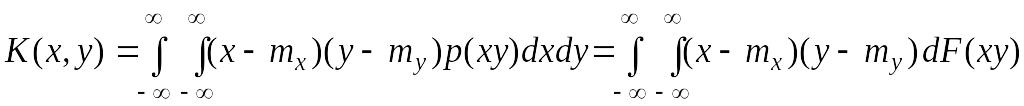Наряду с рассеиванием случайных величин X и Y корреляционный (ковариационный) момент K(x,y) характеризует вероятностную линейную зависимость между ними.

Часто вместо K(x,y) пользуются безразмерной величиной , называемой коэффициентом корреляции:

, ,

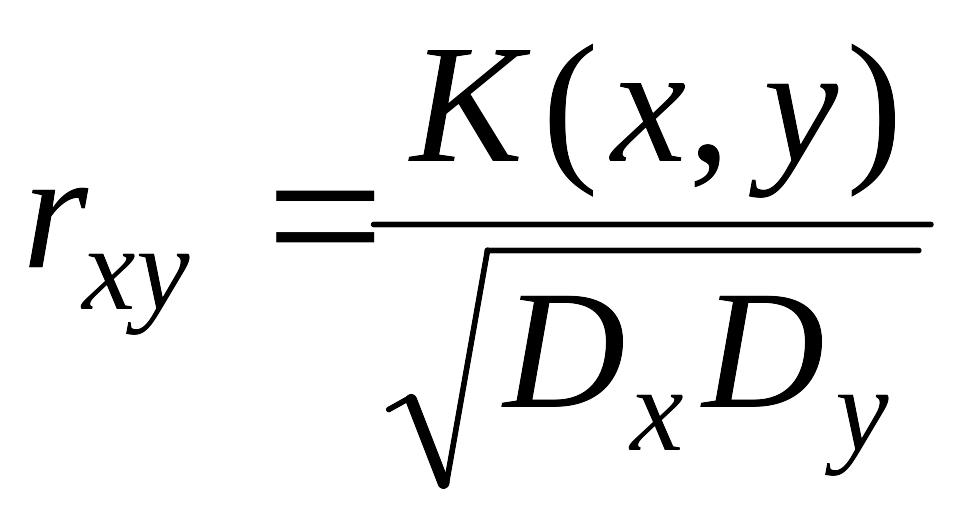который определяет степень линейной вероятностной зависимости между случайными величинами X и Y.

Случайные величины X и Y называются независимыми (некоррелированными), если K(x,y) = 0 или = 0.

Математическое ожидание m и дисперсия D (или среднее квадратическое отклонение) – наиболее часто применяемые характеристики случайной величины.

Дисперсия имеет следующие основные свойства:

1. Дисперсия – величина неотрицательная: D[X] ≥ 0. При X = C,

где С – постоянная величина, дисперсия равна нулю: D[C] = 0.

2.Постоянный множитель С можно выносить за знак дисперсии, возводя его в квадрат:

D[CX] = D[X].

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

D[ + ] = D[ ] + D[ ].

Это свойство распространяется на случай произвольного числа слагаемых независимых случайных величин.

4. Дисперсия суммы (разности) постоянной величины С и случай-ной величины X равна дисперсии случайной величины:

D[С – X] = D[X ].

5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

D[X – Y] = D[X ] + D[Y].

6. Дисперсия суммы двух зависимых случайных величин равна

D[X + Y] = D[X ] + D[Y ] + 2K(x,y).

Третий центральный момент служит для характеристики асимметрии (или скошенности) распределения случайной величины относительно математического ожидания.

Для оценки скошенности распределения используют безразмерный коэффициент асимметрии А

А = .

Если А > 0 , то кривая распре-деления смещена влево относитель-но математического ожидания . Если А < 0 , то кривая распределе-ния смещена вправо относительно математического ожидания .. (рис.5.4).

Четвертый центральный момент служит для характеристики "крутости" распределения случайной величины (рис.5.5).

Это свойство распределения описывается коэффициентом эксцесса Е распределения случайной величины, определяемого по формуле

Е = .

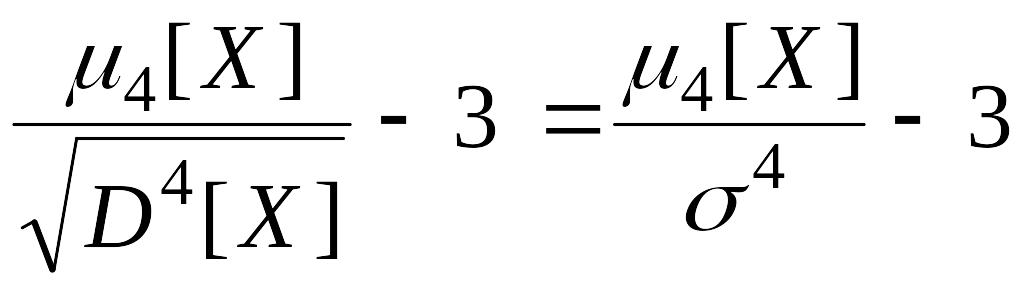К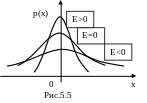 оэффициент эксцесса Е характеризует крутость распределения относительно нормального закона распределения, для которого

Е = .

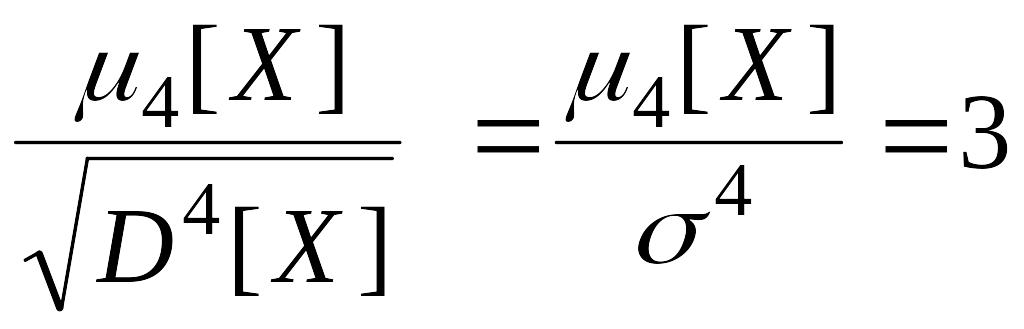Если E < 0, то распределение «пологое». При E > 0 распределение «островершинное», а при E = 0 распределение «нормальное».

Числовые характеристики случайных величин достаточно просто находить при помощи характеристической функции. Дифференцируя по u, получим:

.

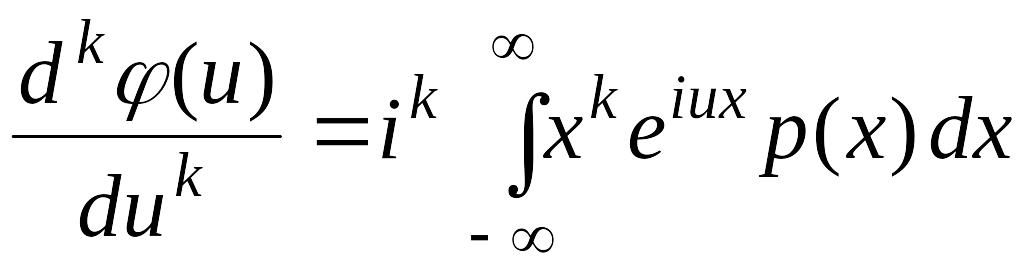Положив u = 0 , получаем простую связь между значениями производной характеристической функции при u = 0 и начальными моментами:

.

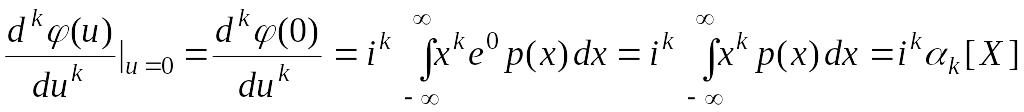Отсюда

.

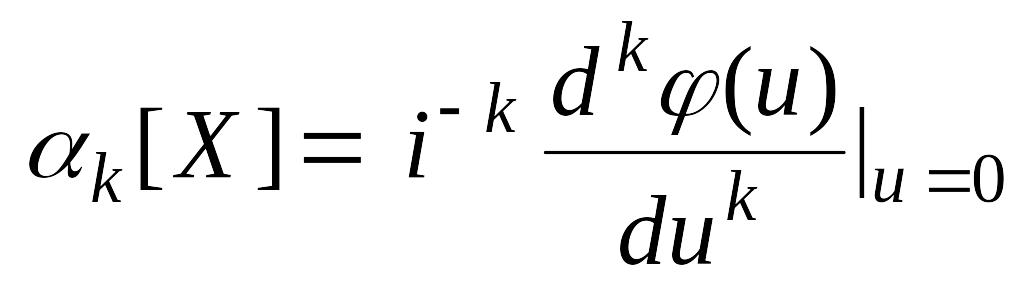Эта формула дает простой способ вычисления начальных моментов путем дифференцирования характеристической функции.

Для нахождения центральных моментов используют натуральный логарифм характеристической функции. Эту функцию называют логарифмической характеристической функцией.