Сохранение углового момента

Симметрия в физике
Преобразования	Инвариантность	Закон сохранения
↕ трансляции времени	Консервативность	…энергии
↔ изотропия времени	Изотропия времени	…энтропии
↔ трансляции пространства	Однородность	…импульса
○ Вращения	Изотропность пространства	…момента импульса
× Группа Лоренца	Относительность Лоренц-инвариантность	…интервала

Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

Производная момента импульса по времени есть момент силы:

Таким образом, требование системы быть «замкнутой», означает равенство нулю главного (суммарного) момента внешних сил:

где  — момент одной из сил, приложенных к системе частиц.

Математически закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол , радиус-вектор частицы с номером изменятся на , а скорости — . Функция Лагранжа системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому

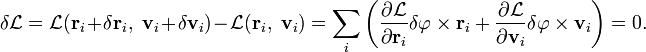
С учетом , где  — обобщенный импульс -той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде

Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:

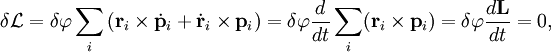
где,  — момент импульса системы. Ввиду произвольности , из равенства следует .

На орбитах момент импульса распределяется между собственным вращением планеты и момента импульса ее орбитального движения:

Момент импульса в электродинамике

При описании движения заряженной частицы в электромагнитном поле, канонический импульс не является инвариантным. Как следствие, канонический момент импульса тоже не инвариантен. Тогда берем реальный импульс, который также называется «кинетическим импульсом»:

где  — электрический заряд,  — скорость света,  — векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы m в электромагнитном поле:

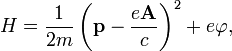
где  — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса или «кинетический момент импульса» определяется:

Момент импульса в квантовой механике Оператор момента

В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определенными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на (h с чертой), определяемой, как постоянная Планка, поделенная на 2π. Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновой момент импульса всегда кратен . Например, электрон в состоянии покоя имеет момент импульса .

В классическом определении момент импульса зависит от 6 переменных , , , , , и . Переводя это на квантовомеханические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и его компоненты по осям.

Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:

где и  — координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

где  — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:

и даже более важные подстановки с гамильтонианом частицы без заряда и спина: