Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

Характеристики вращения тела

При равномерном вращении (T оборотов в секунду),

• Частота вращения — число оборотов тела в единицу времени.

• Период вращения — время одного полного оборота. Период вращения T и его частота ν связаны соотношением T = 1 / ν.

• линейная скорость точки, находящейся на расстоянии R от оси вращения

,

• угловая скорость вращения тела

.

• Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.

• Кинетическая энергия вращательного движения

где I_z — момент инерции тела относительно оси вращения. ω — угловая скорость

Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью определяется формулой:

где  — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = rω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.

• Производная угловой скорости по времени есть угловое ускорение.

• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).

• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).

• В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где  — радиус-вектор точки (из начала координат),  — скорость этой точки.  — векторное произведение,  — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

• При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц) (то есть в таких единицах ).

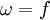• В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так:

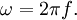
• Наконец, при использовании градусов в секунду связь с частотой вращения будет:

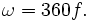
Угловое ускорение — векторная величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, когда его угловая скорость ω растёт (или убывает) равномерно, численно угловое ускорение:

Вектор углового ускорения α направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени, то есть , и направлен по касательной к годографу вектора в соответствующей его точке.

Связь между линейным ускорением и угловым ускорением: а = * R ,где R - радиус окружности

Основная задача динамики Основная задача динамики

• Прямая задача динамики: по заданным силам определить характер движения тела!!!

• Обратная задача динамики: по заданному характеру движения определить действующие на тело силы.

• Прямая задача динамики: по заданным силам определить характер движения тела!!!

Обратная задача динамики: по заданному характеру движения определить действующие на тело силы.

Исаак Ньютон задался целью описать движение объектов, используя понятия инерции и силы. Сделав это, он попутно установил, что всякое механическое движение подчиняется общим законам сохранения. В 1687 г. Ньютон опубликовал свой знаменитый труд «Математические начала натуральной философии», в котором изложил три основополагающих закона классической механики (знаменитые законы Ньютона).

Зако́н ине́рции или Первый закон Нью́тона: любое свободное тело, на которое не действуют силы со стороны других тел, находится в состоянии покоя или равномерного прямолинейного движения (понятие скорости здесь применяется к центру масс тела в случае непоступательного движения). Иными словами, телам свойственна ине́рция (от лат. inertia — «бездеятельность», «косность»), то есть явление сохранения скорости, если внешние воздействия на них скомпенсированы.

Первый закон Ньютона в современной формулировке звучит так:

Cуществуют такие системы отсчёта, относительно которых любое тело (материальная точка) при отсутствии на него внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения

Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). Все другие системы отсчёта называются соответственно неинерциальными. Проявлением инерции в них является также возникновение фиктивных сил инерции.

Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив закон инерции: любое тело, на которое не действуют внешние силы или действие этих сил компенсируется, находится в состоянии покоя или равномерного прямолинейного движения.

Всякая система отсчёта, движущаяся относительно ИСО равномерно и прямолинейно, также является ИСО. Согласно принципу относительности, все ИСО равноправны, и все законы физики инвариантны относительно перехода из одной ИСО в другую. Это значит, что проявления законов физики в них выглядят одинаково, и записи этих законов имеют одинаковую форму в разных ИСО.

Предположение о существовании хотя бы одной ИСО в изотропном пространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга со всевозможными постоянными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласно теореме Нётер, однородность пространства относительно сдвигов даст закон сохранения импульса, изотропность приведёт к сохранению момента импульса, а однородность времени — к сохранению энергии движущегося тела.

Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея.

В специальной теории относительности скорости относительного движения ИСО, реализуемых действительными телами, не могут превышать некоторой конечной скорости «C» (скорость распространения света в вакууме) и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца.

Абсолютно инерциальные системы представляют собой математическую абстракцию, естественно, в природе не существующую. Однако существуют системы отсчёта, в которых относительное ускорение достаточно удалённых друг от друга тел не превышает 10^-10 м/с², например, Международная небесная система координат в сочетании с Динамическим временем дают систему, относительные ускорения в которой не превышают 1,5·10^-10 м/с² (на уровне 1σ)^[1]. Точность экспериментов по анализу времени прихода импульсов от пульсаров, а вскоре — и астрометрических измерений, такова, что в ближайшее время должно быть измерено ускорение Солнечной системы при её движении в гравитационном поле Галактики, которое оценивается в м/с^2[2].

С разной степенью точности и в зависимости от области использования инерциальными системами можно считать системы отсчёта, связанные с: Землёй, Солнцем, неподвижные относительно звезд.