1.2 Аналіз методу сортування Шелла
Для
алгоритму сортування, який кожного разу
переміщує запис тільки на одну позицію,
середній
час буде в кращому випадку пропорційно
N2,
тому що в процесі сортування кожна запис
повинна пройти в середньому
позицій. Тому, якщо бажано отримати
метод, істотно перевершує по швидкості
метод простих вставок, необхідний
механізм щоб записи могли переміщатися
великими стрибками, а не короткими
кроками. Такий метод запропонований в
1959 році Дональдом Л. Шеллом [Donald L. Shell,
CACM 2,7 (Java, 1959), 30-32] і відомий у всьому світі
під ім'ям свого автора. Нехай є масив
записів R1, R2, ...., R16. Ділимо 16 записів на
8 груп по два записи в кожній групі: (R1,
R9), (R2, R10), ...., (R8, R16). Сортуємо вибрані пари
записів у порядку, наприклад, зростання,
тобто якщо в парі (R2, R10): R2> R10, то R2 і R10
міняємо місцями: R1, R10, R3, R4, R5, R6, R7, R8, R9,
R2, R11, R12, R13, R14, R15, R16. Те ж саме виконується
і для інших пар записів. Це сортування
із зсувом 8. Цей процес називається
першим проходом. Розділимо тепер запису
на чотири групи по чотири записи в
кожній: (R1, R5, R9, R13), ..., (R4, R8, R12, R16). Потім
знову розсортуємо кожну групу окремо.
Це сортування із зсувом 4. На третьому
проході відсортуємо 2 групи по 8 записів:
(R1, R3, R5, R7, R9, R11, R13, R15) і (R2, R4, R6, R8, R10, R12,
R14, R16). Це сортування із зсувом 2. Процес
завершується четвертим проходом, під
час якого сортуються всі 16 записів. Це
сортування із зсувом 1. У кожній з
проміжних стадій сортування беруть
участь або порівняно короткі масиви,
або вже порівняно добре впорядковані
масиви, тому на кожному етапі можна
користуватися методом простих вставок.
Метод сортування Шелла ще називається
з «убутним зміщенням», оскільки кожен
прохід характеризується зміщенням h,
таким, що сортуються записи, кожна з
яких відстоїть від попередньої на h
позицій. Послідовність значень зміщень
8, 4, 2, 1 не слід вважати незмінною, можна
користуватися будь-якою послідовністю
зсувів, але останнім зсув має дорівнювати
Алгоритм базується на двох тезах:
Сортування включенням ефективне для майже впорядкованих масивів.
Сортування включенням неефективне, тому що переміщує елемент тільки на одну позицію за раз.
Тому сортування Шелла виконує декілька впорядкувань включенням, кожен раз порівнюючи і переставляючи елементи, що розташовані на різній відстані один від одного.
Сортування Шелла не є стабільним.
Після цього весь масив сортується разом. За рахунок попередніх етапів він виявляється вже близьким до відсортованого, тому обмінів необхідно вже не так багато.
Аналіз та експериментальні дослідження методу показують, що цей метод дає кращі результати, якщо розподіл на підмасиви роблять кроками, що не є степенями двійки, а, навпаки, не є множниками один одного.
Далі, на прикладі послідовності цілих чисел, показаний процес сортування масиву методом Шелла. Для зручності і наочності, елементи однієї групи виділено однаковим кольором.
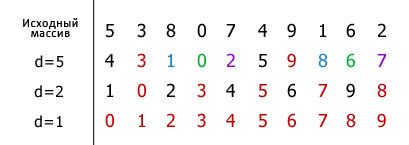
Перше значення , відповідне віддалі d одно 10 / 2 = 5 . На кожному кроці воно зменшується вдвічі. Елементи, що входять в одну групу , порівнюються і якщо значення якого-небудь елементу , що стоїть лівіше того з яким він порівнюється , виявляється більше ( сортування за зростанням ) , тоді вони міняються місцями. Так , елементи шляхом внутрішньогрупових перестановок поступово стають на свої позиції , і на останньому кроці ( d = 1 ) сортування зводиться до проходу по одній групі, що включає в себе всі N елементів масиву. При цьому число необхідних обмінів виявляється зовсім невеликим.