Графическое определение константы Михаэлиса (Кm)

Графически константа Михаэлиса может быть представлена, как это показано на рис. 6.1. Однако в случае многих ферментов определение V_max и К_M непосредственно из графика зависимости V₀ от [S] (рис. 6.1) оказывается затруднено. Для большего удобства уравнение Михаэлиса-Ментен было преобразовано Лайнуивером и Берком в координатах двойных обратных величин:

Правую часть уравнения представляют в виде суммы двух слагаемых:

Упростив уравнение, получаем:

Как можно видеть, это уравнение представляет собой уравнение прямой:

у = ах + b,

где у = 1/V₀ и х = 1/[S].

Если построить график зависимости у (т.е. 1/V₀) от х (т.е. 1/[S]), то длина отрезка b, отсекаемого на оси у, будет равна 1/V_max, а тангенс угла наклона – а равен величине K_M/V_max. Длину отрезка, отсекаемого на оси х (в области отрицательных значений), можно получить, приравняв к нулю. Тогда получим:

График уравнения Михаэлиса-Ментен в обрат­ных координатах называют графиком Лайнуивера-Берка (рис. 6.2). Используя его, величину K_M можно определить либо по наклону прямой и длине отрезка, отсекае­мого на оси у, либо по длине отрезка, отсекаемого в области отрицательных значений на оси х. Поско­льку [S] измеряют в молях/литр, K_M имеет ту же размерность. Скорость V₀ мо­жет быть выражена в любых единицах, поскольку K_M не зависит от [E]. График Лайнуивера-Берка позволяет определять K_M по отно­сительно небольшому числу точек, поэтому он часто используется для расчета этого параметра.

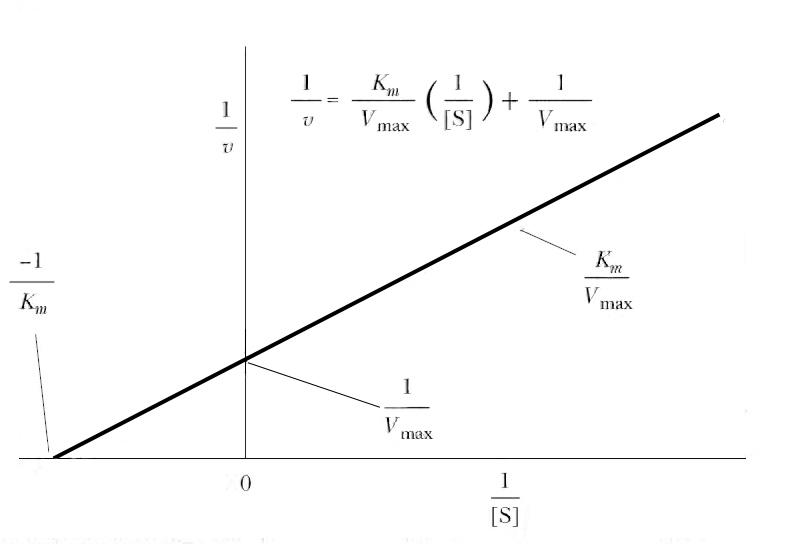
Рис. 6.2

График Лайнуивера-Берка в двойных обратных координатах (зависимость 1/V0 от 1/[S]), используемый для графического определения KM и Vmax.

Используя график Лайнуивера-Берка на прак­тике, при определении K_M, иногда сталкиваются с тем, что почти все точки оказываются в области низких кон­центраций субстрата. Это происходит в тех случаях, когда измерения проводят через равные интервалы [S]. Чтобы этого избежать, измерения следует прово­дить при таких значениях [S], которые соответ­ствуют равным интервалам на оси х в обратных ве­личинах.

Еще одним вариантом линеаризации зависимости скорости ферментативной реакции от концентрации субстрата является преобразование Хейнса-Вулфа. Если в уравнении Михаэлиса-Ментен в обрат­ных координатах

обе части умножить на величину [S], получим:

или

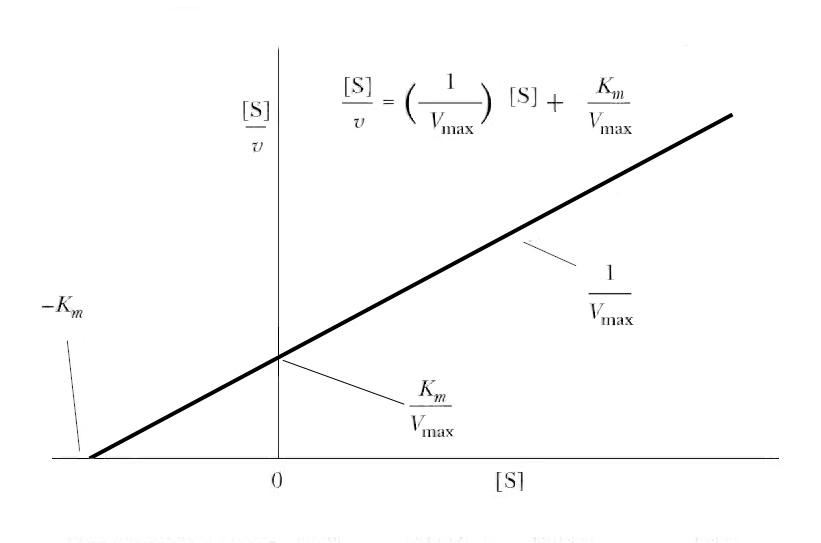
Рис. 6.3

График Хейнса-Вулфа в координатах [S]/V0 от [S], используемый для графического определения KM и Vmax.

График зависимости [S]/V₀) от [S] (рис. 6.3) представляет собой прямую линию, где тангенс угла наклона равен величине 1/V_max, длина отрезка, отсекаемого на оси у, будет равна K_M/V_max, а отрезок, отсекаемый на оси х, равен величине

–K_M.

Определение K_M имеет большую практическую ценность. При концентрациях субстрата, в 100 раз превышающих K_M, фермент будет работать практически с макси­мальной скоростью, поэтому максимальная скорость, V_max, будет отражать количество присутствующе­го активного фермента. Это немаловажное обстояте­льство используют для оценки содержания фермен­та в препарате. Знание величины K_M позволяет определить, какое количество субстрата следует внести в реакционную смесь для определения V_max. Графики, построенные в обратных координатах, находят широкое примене­ние также при анализе характера действия ингибиторов в ферментативных реакциях.