16. При каких условиях возникают картины муара?

Муаровый узор появляется при интерференции структур с близкими периодами решеток. Вклад в изображение дает пучок дифрагировавший по одному разу от плоскостей включения с межплоскостным расстоянием d₁ и от плоскостей матрицы с d₂. Пучок дифрагирует от верхней части образца и потом дифрагирует как первичный на нижней части.

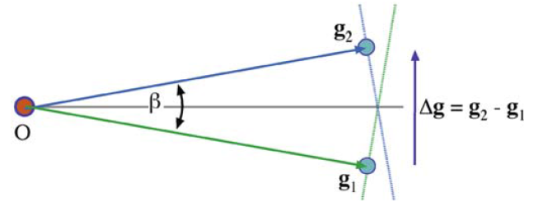
|Δg|^-1 – разность периодов решетки.

17. Чем муар отличается от прямого разрешения решетки?

Основным отличием муара от прямого разрешения является фактор порождающий данные виды изображений. В первом случае это включения второй фазы с близким межплоскостным расстоянием к первой (экстинкционный матричный контраст), а во втором случае это несовершенства кристаллической структуры не связанные с включениями (дислокации, границы блоков - субзерен) (фазовый контраст) (следы атомных плоскостей).

18. На каких элементах структуры происходит рассеяние электронных волн?

Рассеяние происходит на атомных плоскостях.

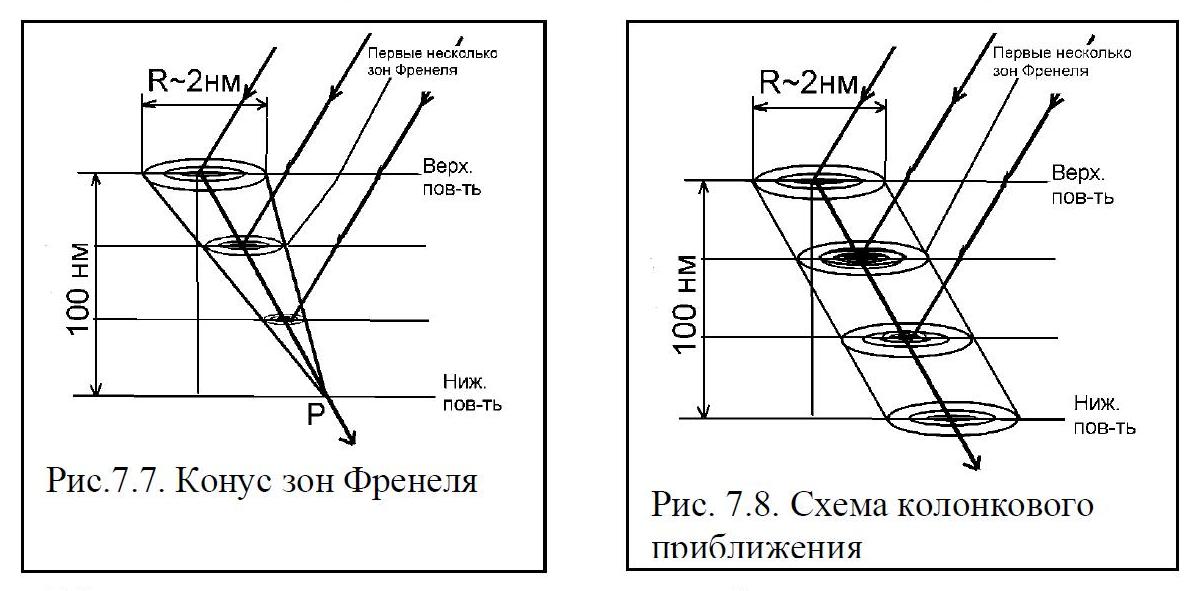
19. В чем состоит колонковое приближение? Почему оно характерно для электронной микроскопии?

Колонковое приближение основывается на том, что амплитуда выходящей из образца волны определяется вкладом всех ячеек образца, лежащих в конусе, с угловым раствором, определяемым несколькими зонами Френеля, диаметр которых, в свою очередь определяется длиной волны, т.е. кристалл разбивается на разные ячейки которым соответствуют свои колонки. Малый размер длины волны (следовательно малые радиусы зон Френеля) приводит к малым ВБ углам при дифракции быстрых электронов (для металлов Θ~10^-2 рад) конус оказывается настолько острым, что можно считать, что плотность электронов в каждой точке нижней поверхности образца определяется рассеянием электронов вдоль колонки или столбика из элементарных ячеек над этой точкой. Колонковое приближение не канает, при отражениях высоких порядков, значительной толщине кристалла и более высоких требованиях к разрешению (<2нм).

20. В чем состоит кинематическое приближение? Когда оно реализуется?

При кинематическом приближении используются следующие приближения: 1) Элементарная ячейка состоит из сферических симметричных атомов; 2) Атомы неподвижны, т.е. тепловые колебания отсутствуют; 3) Все элементарные ячейки – одинаковы, т.е. кристалл – бездеффектный; 4) Рассеянная один раз волна выходит из кристалла, т.е. рассеяние является однократным; 5) Нет интерференции между падающей и рассеянной волной.

Соответственно кинематическая теория работает при больших отклонениях от ВБ положения (нет дополнительной дифракции), малой толщине образца (волна не успевает рассеяться многократно) и отсутствии в нем деффектов.

Не учитывает взаимодействия дифрагированного пучка с кристаллом и прямым пучком, поэтому применима для достаточно тонких кристаллов или в случае больших отклонение кристалла от отражающего положения. При этом интенсивность дифрагированного луча значительно меньше интенсивности первичного.

21. Каков период угловых осцилляций интенсивности при выполнении кинематического приближения?

Период угловых осцилляций при кинематическом приближении: 1/kz, где z – атомный номер, k=2π/λ – волновой вектор. Период зависит от заряда ядра↑, экстинкции↓, плотности заполнения, потенциала↑, рассеяния электронов↑.

22. Каков период толщинных осцилляций интенсивности при выполнении кинематического приближения?

Период толщинных осцилляций при кинематическом приближении: 1/kε_g , где k=2π/λ – волновой вектор, ε_g = s – вектор несовпадения.

23. Какое приближение называется двухлучевым? В чем суть упрощений волновых уравнений при двухлучевом приближении?

Когда кинематическая теория перестает работать, в бой вступает многолучевое приближение динамической теории. Принимается, что изображение формируется только двумя сильными волнами (000 и HKL обратной решетки на сфере Эвальда), остальными при этом – пренебрегают. Используется для ограничения числа слагаемых в бесконечном ряде волнового уравнения.

24. Запишите уравнения Хови-Вилана для идеального кристалла в двухлучевом приближении и расшифруйте использованные обозначения.

Уравнение Хови-Уиллана для совершенного кристалла в двухлуч. приближении имеет вид:

1. ;

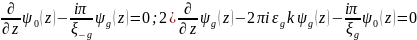1/ξ_±g = (-2m/h²k)U_±g – длина рассеяния на плоскости (ξ_±g – длина экстинкции); ψ₀(z) – амплитуда падающего пучка, ψ₀(z) – амплитуда дифрагированного пучка; образец делится на толщины dz – соответственно z - координата. Уравнение 2 описывает вклад рассеяния в прямом направлении, а уравнение 1 – вклад брэгговского рассеяния.