Тема 2.6 Кручение

1. Что называется кручением?

Кручением называется деформация, при которой в поперечном сечении бруса возникает крутящий момент.

2. Что называется крутящим моментом?

Крутящий момент – это ВСФ, численно равный алгебраической сумме вращающих моментов, взятых с одной стороны от сечения.

3. Как выглядит расчетная схема элемента конструкции при кручении?

Элемент конструкции нагружен вращающими моментами, алгебраическая сумма которых равна нулю.

4. Как может определяться вращающий момент?

Т = F_t , где F_t – окружная сила, d – диаметр, T = , где Р – мощность, ω – угловая скорость.

5. Что называется эпюрой крутящих моментов?

Эпюра крутящих моментов – это график изменения вращающих моментов по длине элемента конструкции.

6. Что называется опасным участком для бруса постоянного поперечного сечения?

Опасным участком для бруса постоянного поперечного сечения называется участок с максимальным крутящим моментом.

7. Как распределяются касательные напряжения по поперечному сечению?

Касательные напряжения по поперечному сечению распределяются неравномерно – в центре равны нулю, на периферии достигают максимального значения.

8. Как определяются максимальные напряжения в поперечном сечении бруса и в опасном сечении?

- в поперечном сечении, - в опасном сечении

9. Как изменится напряжение в поперечном сечении бруса, если: а) диаметр бруса увеличить в два раза; б) изменить материал бруса? Почему?

Напряжение в поперечном сечении бруса определяется по формуле

.

а) При увеличении диаметра бруса в два раза, полярный момент сопротивления увеличится в 8 раз, значит, напряжение в 8 раз уменьшится.

б) Материал при кручении характеризует модуль сдвига G, которого нет в данной формуле, значит, напряжение не изменится.

10. Какой параметр определяет жесткость бруса при кручении и как он определяется?

За меру жесткости при кручении принимают относительный угол закручивания (угол закручивания на единицу длины), определяемый по формуле

или полный угол закручивания

11. Как изменится угол закручивания бруса, если при прочих равных условиях увеличить диаметр бруса в два раза? Почему?

Угол закручивания бруса определяется по формуле . При увеличении диаметра бруса в два раза, полярный момент инерции увеличится в 16 раз, значит, угол закручивания уменьшится в 16 раз, т.е. жесткость в 16 раз увеличится.

12. Почему выгоднее применять валы кольцевого, а не сплошного поперечного сечения?

При равных площадях поперечного сечения кольцевое сечение обладает большими полярными моментами инерции и сопротивления, чем сплошное, т.е. вал кольцевого сечения оказывается жестче и прочнее. Наконец, при равной прочности и равной жесткости, т.е. при одинаковых значениях Wр или Jр , полый вал получается легче сплошного.

Условие прочности при кручении по опасной точке:

, МПа

где допускаемое напряжение, принимается в пределах 20 - 40 МПа, в связи с тем, что расчеты на кручение, как ориентировочные, ведутся без учета деформации изгиба и концентрации напряжений.

Данное условие прочности позволяет выполнить три вида расчетов:

4. Проверочный ,

5. Проектировочный

6. Определение допустимой нагрузки

Условие жесткости при кручении по относительному углу закручивания может быть представлено в разных единицах измерения и также позволяет выполнить соответствующие виды расчетов:

, рад/м

1. Проверочный

2. Проектировочный

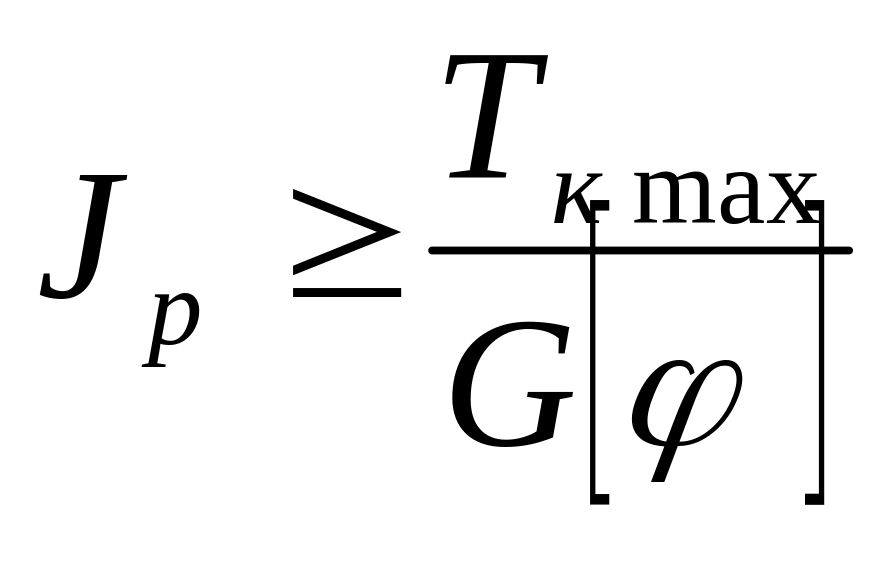
3. Определение допустимой нагрузки

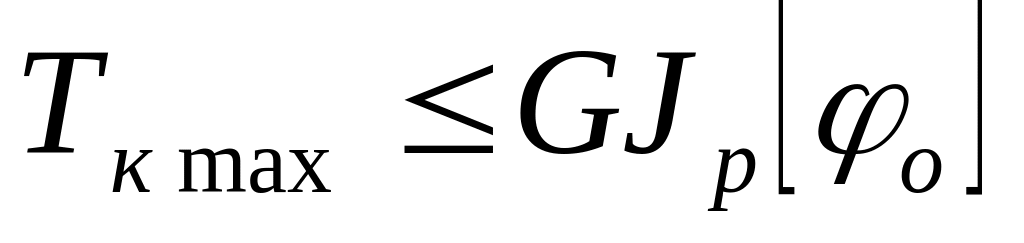
град/м

1. Проверочный

2. Проектировочный

3. Определение допустимой нагрузки

Допускаемые значения относительных углов закручивания

= (4,38-17,5) · 10^-3 рад/м или = 0,25 – 1 град/м.

При выполнении одновременно двух видов расчета по определению геометрических размеров или допустимой нагрузки из условий прочности и жесткости, за окончательные значения принимают соответственно большее и меньшее значение определяемого параметра.

Задача 20. (Образец выполнения практической работы для защиты модуля 3 и 4)

Стальной вал (G = 8· 10⁴ МПа) постоянного поперечного сечения (рис.1) вращается с угловой скоростью ω = 25 рад\с. Мощности, снимаемые с рабочих шкивов: Р₁ = 38 кВт, Р₂ = 30 кВт, Р₃ = 22 кВт. Определить диаметр вала из расчета на прочность и жесткость при кручении, если допускаемое напряжение [τ_к] = 30 МПа, допускаемый относительный угол закручивания [φ₀] = 7∙ 10^-3 рад/м.

Рис.1 Схема вала

1.Определить вращающие моменты на рабочих шкивах

2. Определить вращающий момент, передаваемый валу от электродвигателя

3. Составить расчетную схему вала (рис.2,а)

Рис.2 Расчетная схема вала (а) и эпюра крутящих моментов (б)

4.Определить крутящие моменты, и построить по ним эпюру крутящих моментов (рис. 2,б)

Т_к1 =

Т_к2 =

Т_к3 =

Опасный участок: Т_кmax =

4.Определить диаметр вала по опасному участку из расчета на прочность при кручении

5.Определить диаметр вала по опасному участку из расчета на жесткость при кручении

6.Принять за окончательный диаметр больший из двух расчетных, округлив его до целого числа, оканчивающегося на 0, 2, 5, 8.

d =

Задача 21. Выполнить условие задачи 11, изменив в ней расположение шкивов на расчетной схеме (рис.1,а)

Рис.1 Расчетная схема вала (а) и эпюра крутящих моментов (б)

1. Определить крутящие моменты, и построить по ним эпюру крутящих моментов (рис. 2,б)

Т_к1 =

Т_к2 =

Т_к3 =

Опасный участок: Т_кmax =

2. Определить диаметр вала по опасному участку из расчета на прочность при кручении

3 Определить диаметр вала по опасному участку из расчета на жесткость при кручении

4 Принять за окончательный диаметр больший из двух расчетных, округлив его до нормального значения.

d =

Задача 22. Вал передает мощность Р = 16 кВт при угловой скорости ω = 158 рад\с. Проверить прочность стального вала, если его диаметр d = 35 мм и допускаемое напряжение [τ_к] =30 МПа.

Вид расчета –

Расчетная формула

Задача 23. Определить из расчета на прочность при [τ_к] = 40 МПа требуемый диаметр вала передающего мощность Р = 48 кВт при частоте вращения n = 970 об\мин.

Вид расчета –

Расчетная формула

Задача 24. Определить из расчета на прочность требуемые размеры поперечного сечения вала (рис.1,а) в двух вариантах: - круг; - кольцо с отношением внутреннего диаметра к наружному α = 0,7. Сечение вала считать по всей длине постоянным. Принять =25 МПа = 5,3·10^-3 рад\м. Сравнить, какой из этих валов экономичнее и во сколько раз.

Решение:

1. Определить неизвестный вращающий момент

2.Определить крутящие моменты, и построить по ним эпюру крутящих моментов (рис. 2,б)

Т_к1 =

Т_к2 =

Рис.1 Расчетная схема вала (а) и эпюра крутящих моментов (б)

Опасный участок: Т_кmax =

3.Определить диаметр вала по опасному участку из расчета на прочность при кручении

- для круглого сечения

- для кольцевого сечения

4.Определить диаметр вала по опасному участку из расчета на жесткость при кручении

- для круглого сечения

- для кольцевого сечения

5.Принять за окончательные диаметры большие из двух расчетных для круга и кольца, округлив их до целого числа, оканчивающегося на 0, 2, 5, 8.

круга d = кольца d =

6. Определить площади подобранных сечений и сравнить, какое из них экономичнее и во сколько раз.

- для круглого сечения

- для кольцевого сечения