Өзара айқасқан іздеу әдісі.
СОӨЖ өткізу түрлері: тренинг және индивидуалдық жоба жасау.
Әдістемелік ұсыныс: Нақты пән саласында мысал таңдау қажет Сол мысалға білімді пайдалану үлгісін таңдап алып, өзара айқасқан іздеу әдісін қолдану керек.
Бұл тәсілде әртүрлі концептуалды объектілер арасындағы қатынастар ізделінеді де, сұраққа жауап екі түрлі төбе доғалары түйіскен жерден ізделеді. Мысалы, бізде семантикалық тордың мынадай белгісі болса:
Бізге берілген сұрақ: Ержан мен Талғат арасында қандай байланыс бар - деген түрде болса, онда осы тор көмегімен Ержан бұл BK-i деген кітапты Талғатқа берді - деген жауап ала аламыз.
Жалпы семантикалық торлармен білімдерді үлгілеудің жақсы жағына бұл әдіс көмегімен білім элементтері бір бірімен түйіндер (төбелер) мен оларды байланыстыратын доғалар арқылы жалғастыратын құрылым түрін жатқызады.
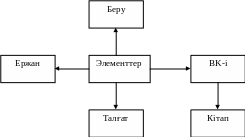
33- сурет. Өзара айқасқан іздеу тәсіліне мысал
Торға енетін ұғымдар мен олардың байланыстары күрделенген сайын, іздеу уақыты ұзарып қиындықтар туындай бастайды. Ол үшін семантикалық торларда мета деңгейінде басқару әдістері бар.
Ұсынылатын әдебиеттер: 3 қос [274-281].
6. Ченг Слейгл әдісі.
СОӨЖ өткізу түрлері: тренинг және индивидуалдық жоба жасау.
Әдістемелік ұсыныс: Нақты пән саласында мысал таңдау қажет. Сол мысалға білімді пайдалану үлгісін таңдап алып, Ченг Слейгл әдісін қолдану керек.
Бұл әдісте кез келген және/немесе графын әдейіленген немесе графына не тармақтың ең аяғында және төбесі бар графқа айналдыруды көздейтін әдіс жолы зерттелген. Бұл айналдыруды іске асыру үшін кез келген және/немесе графы логика формуласы түріне беріліп, оған логика амалдарын қолдану нәтижесінде дизъюнктивтік нормалды форма алынады. Мұндай өзгертілген графқа кейіннен Харт, Нильсон, Рафаэл алгоритмдерін қолдануға мүмкіндік береді.
Ұсынылатын әдебиеттер: 5 нег[110-113], 4 қос [49-64], 5 қос [5-10], 6 қос [3-5].
7. Кілт операторы әдісі.
СОӨЖ өткізу түрлері: тренинг, презентация және индивидуалдық жоба жасау.
Әдістемелік ұсыныс: Нақты пән саласында мысал таңдау қажет. Сол мысалға білімді пайдалану үлгісін таңдап алып, кілт операторы әдісін қолдану керек.
Кез келген <А,В> есебі берілген дейік. Бұл есепке f операторы қолданылған. Бұл операторды қолдану нәтижесінде f(C) күйін алдық дейік. Сонда және – төбесі <А,В> үш балалық төбеге таралады: <A,C> <C,f(C)> <f(C),B>. Соның ішінде ортанғысы – қарапайым есеп болып табылады. Қалған <A,C>, <f(C),B> есептеріне тағы кілт операторын қолдану арқылы оларды да қарапайым есептерге бөлшектеуге болады. Сонымен ең аяғында <А,В> есебін бірнеше қарапайым есептерге бөлшектеуге мүмкіндік болады. Мұнда бір қиындық келтіретін жағдай: қажет болатын кілт операторын табуү Жалпы жағдайда А мен В арасындағы айырмашылық есептелініп, осы айырмашылықты жоюға мүмкіндік беретін оператор ізделінеді.
Ұсынылатын әдебиеттер: 5 нег[35-40], 4 қос [574-579], 5 қос [174-178], 6 қос [5-8].