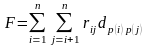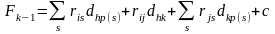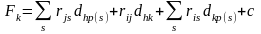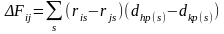Итерационные алгоритмы улучшения начального размещения

Алгоритмы данной группы используют общие идеи методов последовательных приближений. Для этих алгоритмов необходимо знать начальный вариант размещения. Итерационные алгоритмы применяются для решения задачи размещения с различными критериями оптимизации F(p): суммарная длина соединений, суммарное число пересечений соединений и т.д. В любом итерационном алгоритме исследуется некоторое подмножество размещений, в некотором смысле близких к начальному, для выделения в нем размещения с меньшим значением функции-критерия. Найденное размещение вновь принимается за начальное, и процесс повторяется. Алгоритм завершается при отыскании некоторого размещения, в окрестности которого отсутствуют варианты с меньшим значением функции-критерия. В большинстве случаев такой процесс приводит к получению локального минимума функционала F(p).

Различные итерационные алгоритмы размещения имеют сходную структуру, содержащую следующие элементы:

1. преобразование очередного размещения;

2. вычисление функции размещения;

3. выбор лучшего размещения на основе п. 2;

4. переход к следующей итерации и правило останова.

В качестве начального может быть взято размещение, полученное одним из конструктивных алгоритмов размещения, с помощью генератора случайных размещений или заданное конструктором.

Назовем окрестностью очередного размещения множество вариантов, рассматриваемых при выборе лучшего размещения. Иногда это размещения, получаемые из данного попарными или групповыми перестановками элементов. В других случаях это размещения, получаемые при оптимизации мест расположения отдельных элементов, и т.д. В любом случае должно быть определено правило выбора размещения с меньшим значением F(p). При этом могут быть использованы различные тактики, например, выбор на основе максимального уменьшения F(p), или выбор первого размещения с меньшим значением F(p) и т.д.

Из-за отсутствия теоретических оценок эффективности различных итерационных алгоритмов невозможно отдать явное предпочтение одному из них.

Алгоритм парных перестановок

Пусть имеется некоторое размещение (начальное или результат предыдущей итерации). Выбираются два элемента и и меняются местами. Рассчитывается новое значение критерия перестановки F(p) и, если оно меньше предыдущего, то производится обмен; Выбирается другая пара элементов и повторяется аналогичная процедура. Процесс повторяется, пока не будет применено используемое в алгоритме правило остановки.

В качестве иллюстрации рассмотрим минимизацию суммарной длины соединений:

(8.15)

где R=║r_ij║_nxn, D=║d_ij║_nxn, - матрицы смежности и расстояний.

Найдем приращение функции F при перестановке местами элементов е_i и e_j , находящихся первоначально в позициях h и k.

Н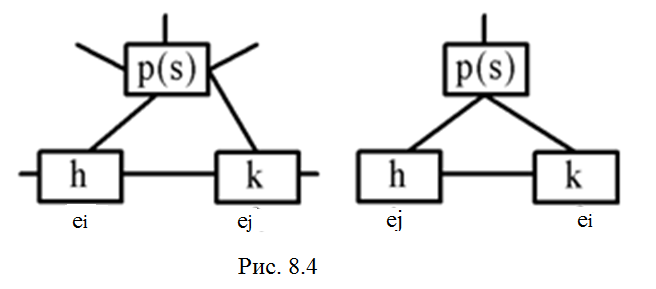 а рис.8.4 показано положение этих элементов до и после перестановки, а также их связь с некоторым элементом е_s (sij) не участвующим в перестановке и находящимся в позиции p(s).

Если длину соединений между всеми парами элементов, не затрагиваемых данной перестановкой, обозначить через с, то получим следующие значения суммарной длины соединений

до перестановки:

(8.16)

после перестановки

(8.17)

вычитая (8.17) из (8.16), получим

(8.18)

Перестановка осуществляется, если F_ij>0.