Правило выбора первого элемента

Необходимо, если отсутствуют размещенные элементы.

При выборе первого элемента можно пользоваться матрицей расстояний. Элементы матрицы расстояний D=║d_ij║_nxn равны расстоянию между центрами позиций l_i и l_j, подсчитанному по одной из формул (8.1) – (8.3). Матрица D симметричная, с нулевой главной диагональю.

Этот элемент является как бы центром группировки. Обычно ищется элемент с наибольшим числом соединений с другими элементами r_i*=max r_i

(8.11)

и помещается в центральную позицию, для которой оценка

(8.12)

минимальна, где d_s –вычисляется по матрице расстояний

Пример

Пусть задан набор позиций для размещения, приведенный на рис. 8.2. Определить центральную позицию для размещения первого элемента.

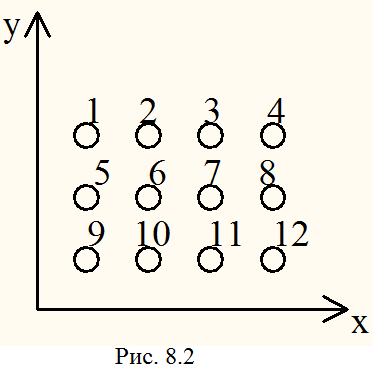
Для этого набора позиций матрица расстояний имеет вид

D =		l1	l2	l3	l4	l5	l6	l7	l8	l9	l10	l11	l12
	l1	0	1	2	3	1	2	3	4	2	3	4	5	d(l1)=30
	l2	1	0	1	2	2	1	2	3	3	2	3	4	d(l2)=24
	l3	2	1	0	1	3	2	1	2	4	3	2	3	d(l3)=24
	l4	3	2	1	0	4	3	2	1	5	4	3	2	d(l4)=30
	l5	1	2	3	4	0	1	2	3	1	2	3	4	d(l5)=26
	l6	2	1	2	3	1	0	1	2	2	1	2	3	d(l6)=20
	l7	3	2	1	2	2	1	0	1	3	2	1	2	d(l7)=20
	l8	4	3	2	1	3	2	1	0	4	3	2	1	d(l8)=26
	l9	2	3	4	5	1	2	3	4	0	1	2	3	d(l9)=30
	l10	3	2	3	4	2	1	2	3	1	0	1	2	d(l10)=24
	l11	4	3	2	3	3	2	1	2	2	1	0	1	d(l11)=24
	l12	5	4	3	2	4	3	2	1	3	2	1	0	d(l12)=30

Для вычисления элементов матрицы использована ортогональная метрика (см. выражение (8.2)), причем расстояние между соседними позициями по вертикали и по горизонтали принято равным 1.

Из подсчета d_s по формуле 8.12 видно, что центральными могут считаться позиции l₆ и l₇.

Можно просмотреть несколько позиций.

Если внешние выводы первого элемента расположены с одной стороны, то эти связи учитывают и смещают элемент в этом направлении.