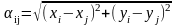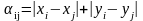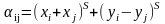Лекция 9 Алгоритмы размещения элементов

Задача размещения элементов в заданных позициях тесно связана с последующей трассировкой соединений. Обычно их решают раздельно.

Формально задача размещения заключается в определении оптимального варианта расположения элементов на плоскости в соответствии с введенным критерием, например, с минимальной взвешенной длиной соединений.

Задача размещения формулируется следующим образом: дано множество конструктивных элементов, связанных между собой цепями в соответствии с принципиальной электрической схемой. Требуется разместить элементы на плоском коммутационном поле, чтобы функционал достигал экстремального значения.

Если элементы конструктивно однотипны, например, микросхемы, то позиции для их размещения фиксированы и находятся в узлах прямоугольной решетки, для которой задается:

• n_x – число позиций в горизонтальном ряду;

• n_y – число позиций в вертикальном ряду;

• h_x – горизонтальный шаг между позициями;

• h_y – вертикальный шаг между позициями;

Могут задаваться, при необходимости, координаты контактных площадок.

Если элементы разногабаритные, то позиции не фиксируются.

В качестве критерия оптимизации чаще всего используют критерий минимума суммарной длины соединений (электрических связей).

Длина соединений подсчитывается по формулам:

	(8.1)	эвклидова метрика
	(8.2)	ортогональная метрика
	(8.3)

S=2, 3, - для минимизации наиболее длинных соединений, т.к. они дадут наибольшее приращение.

Расчет реальных длин проводных соединений на этапе размещения неосуществим практически, т.к. не решена задача разводки цепей.

Наиболее часто используются следующие алгоритмы решения задачи размещения:

1. конструктивные алгоритмы начального размещения;

2. итерационные алгоритмы улучшения начального варианта размещения;

3. непрерывно-дискретные методы размещения;

4. алгоритмы, основанные на решении задач математического программирования.

Конструктивные алгоритмы начального размещения

Наиболее часто используются алгоритмы, использующие последовательный процесс установки элементов в позиции. Рассмотрим один из них:

Пусть имеется множество элементов E=e₁,e₂,…,e_n для размещения и множество позиций L=l₁,l₂,…,l_n для их установки.

Вводится n–шаговый процесс принятия решений, на каждом шаге которого выбирается один из неразмещенных элементов и помещается в одну из незанятых позиций. Структура любого последовательного алгоритма размещения определяется правилом выбора очередного элемента и позиции для его установки.

Пусть Е_к – элементы, размещенные до к-го шага, а L_к – позиции, занятые этими элементами; Е_к и L_к соответственно неразмещенные элементы и незанятые позиции.

Перед началом размещения возможны две ситуации:

1. нет размещенных заранее элементов, тогда должен быть установлен способ выбора и установки первого элемента;

2. имеется группа заранее размещенных элементов.

В основу алгоритмов последовательного размещения заложен эвристический принцип оптимизации целевой функции, когда на шаге выбирается локальная оптимальная позиция для одного элемента при неизменности положения ранее размещенных элементов.

Решение ведется в два этапа: