1.1.4. Многоразрядные сумматоры

В зависимости от характера ввода-вывода кодов и организации переносов многоразрядные сумматоры бывают последовательного и параллельного принципа действия.

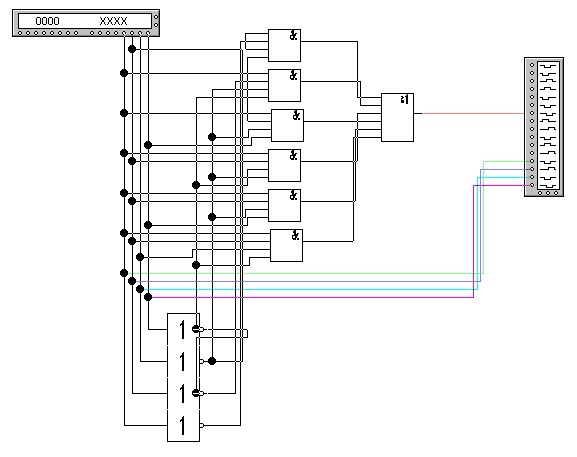
В последовательном сумматоре сложение кодов осуществляется, поразрядно начиная с младшего разряда с помощью комбинационного сумматора на три входа. Образующийся в данном разряде перенос Р_j+1 задерживается на время tэд и поступает на вход P_j сумматора в момент поступления следующего разряда слагаемых. Здесь j специфицирует номер разряда двоичного кода. Таким образом, последовательно разряд за разрядом производиться сложение кодов чисел. Достоинством последовательного сумматора является простота аппаратурной реализации, а недостатком - достаточно большое время суммирования (см. рисунок 11).

В параллельном сумматоре достигается более высокое быстродействие. Суммируемые коды поступают на входы сумматора одновременно по всем разрядам. Для этого в каждом разряде используется комбинационный сумматор на три входа, на выходах которого образуются значения суммы S_j данного разряда и переноса P_j в следующий (старший) разряд. В процессе распространения сигнала переноса устанавливается окончательное значение суммы в каждом разряде. Очевидно, что в течение этого времени на входах сумматора присутствуют сигналы A_j, B_j, соответствующие суммируемым кодам. Максимальное по времени суммирование получается в том случае, когда перенос, возникший в первом разряде, распространяется по всем разрядом (например, при сложении кодов 11..11 и 00..01). В параллельном сумматоре обычно применяются различные способы ускорения переноса (параллельный перенос, групповой и т. п.

Рисунок 11 - Схема трехразрядного последовательного сумматора

1.2 Формирователи (преобразователи) двоичных кодов

Формирователи (преобразователи) двоичных кодов предназначены для преобразования двоичных кодов из одного формата в другой. Для арифметических операционных устройств наиболее типичным является преобразование прямого кода в обратный. Такое устройство в зависимости от управляющего сигнала выдает либо входной код без изменения, либо обратный код. Формирователи обратного кода реализуются на схемах сложения по модулю 2.

1.2.1 Операция вычитания

Использование формирователя обратного кода на входе сумматора позволяет синтезировать универсальную схему для выполнения операций сложения и вычитания в дополнительном коде.

Действительно, если операнды являются числами в дополнительном коде, то на сумматоре можно выполнить операцию вычитания. Для этого на одну входную шину подается обратный код числа, то есть ^B, на вход переноса “1”. Тогда

S =A+ ^ B +1=A+(^B+1) =A+(-B) =A-B

Реализация операции вычитания в дополнительном коде на сумматоре основана на том, что инвертирование кода числа В и прибавление к его младшему разряду единицы эквивалентно смене знака.

2 Цифровые схемы сравнения

Это специальный класс комбинационных элементов, которые на основе подаваемых на них многоразрядных двоичных кодов формируют логические функции. В схемах сравнения функции характеризуют отношение порядка между кодами, то есть отношения больше, меньше, равно и производные от них >=, <=, <>. Схемы сравнения не имеют управляющих сигналов.

В связи с тем, что одновременно формируются сигналы нескольких отношений, схема сравнения может иметь несколько выходов, каждый их которых соответствует своему отношению.

Частным и более простым вариантом схем сравнения являются схемы сравнения с нулем.

Цифровые схемы сравнения формируют на выходе F=1 при равенстве подаваемых на вход двух двоичных чисел А (поразрядно записываем a и b) и В (c и d). Цифровая схема сравнения это цифровой аналог компаратора (см. рисунок 12), являющегося одним из важнейших устройств импульсной техники, временная диаграмма схемы сравнения приведена на рисунке 13. На основе таблицы истинности для компаратора составим уравнения (для A>B, A<B, A=B), минимизируем их, используя законы алгебры логики (см. таблицу 4).

Рисунок 12 - Цифровая схема сравнения