Приложение № 1 мгту им. Н.Э. Баумана

Домашнее задание №2

по ТЕРМОДИНАМИКЕ

«ТЕРМОДИНАМИЧЕСКИЙ АНАЛИЗ ГАЗОВОГО ЦИКЛА»

Группа: Э5-51

Вариант: 29

Студент: Иванов И.И.

Преподаватель: Петров П.П.

Москва 2013 г.

Домашнее задание №2 по курсу «ТЕРМОДИНАМИКА»

«ТЕРМОДИНАМИЧЕСКИЙ АНАЛИЗ ГАЗОВОГО ЦИКЛА»

Дано:

Сухой воздух массой 1 кг совершает прямой термодинамический цикл (Рис. 1), состоящий из четырех последовательных термодинамических процессов, параметры которых определяются преподавателем.

Требуется:

1) рассчитать давление (p), удельный объем (v) и температуру (T) воздуха для основных точек цикла,

2) определить для каждого из процессов значения показателей политропы (n) и теплоемкости (c), вычислить изменение внутренней энергии (u), энтальпии (h), энтропии (s), теплоту процесса (q), работу процесса (l) и располагаемую работу (l₀),

3) определить суммарные количества подведенной (q') и отведенной (q'') теплоты, работу цикла (l_ц), располагаемую работу цикла (l_0ц) и термический к.п.д. цикла (_t),

4) построить цикл в координатах:

а) lg v – lg p,

б) v – p, используя предыдущее построение для нахождения трех или четырех промежуточных точек на каждом из процессов,

в) s – Т, нанеся основные точки цикла и составляющие его процессы,

5) для одного из процессов цикла, кроме изотермического, привести схему его графического расчета по тепловой s – T диаграмме, изобразив на схеме линию процесса вспомогательные линии изохорного и изобарного процессов, значения температур в начале и в конце процесса, отрезки, соответствующие изменению энтропии в основном и вспомогательных процессах, площади, соответствующие теплоте процесса, изменению внутренней энергии и энтальпии.

Вариант 29

Дано:

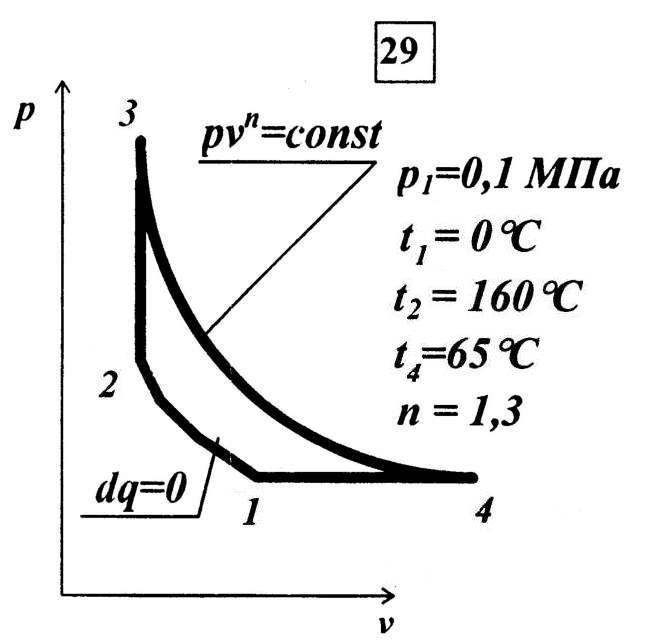
Рис. 1

p₁ = 0,1 МПа = 1 ;

T₁ = 273 K; (t₁ = 0 ⁰С)

T₂ = 433 K; (t₂ = 160 ⁰С)

T₄ = 338 K; (t₄ = 65 ⁰С)

n = 1,3 – показатель политропы

теплоемкости процессов:

c_р = 1,025 ;

c_v= c_р - R =1,025 - 0,287 = 0,738 ;

R = 0,287 ; - газовая постоянная воздуха.

Решение.

1. Определить параметры p, v и T воздуха для основных точек цикла:

а) для точки 1 дано: p₁=0,1 (1 ); T₁ = 273 K; (t₁ = 0 ⁰С)

Для определения v₁ используем уравнение состояния:

v₁ = , ;

б) для точки 2 дано: T₂ = 433 K; (t₂ = 160 ⁰С);

– определить p₂ и v₂. Для определения v₂ используем уравнение адиабаты процесса 1 – 2 в T–v координатах: , где

- показатель адиабаты

или

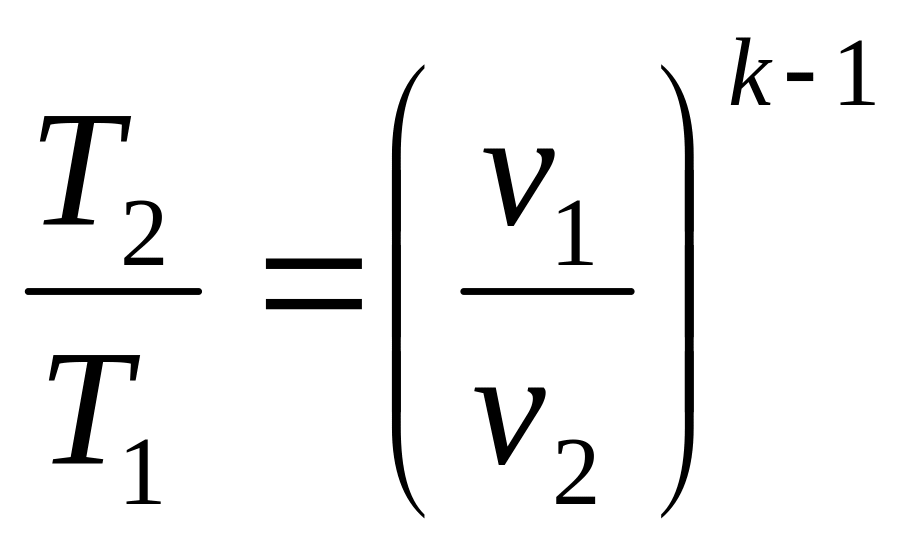
откуда

, ;

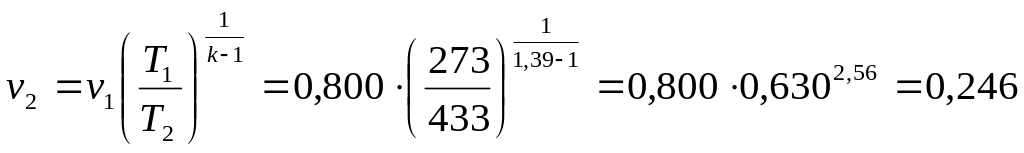Для определения p₂ используем уравнение состояния:

откуда

, Па

в) для точки 4 дано: T₄ = 338 K; (t₄ = 65 ⁰С); p₄ = p₁ = 0,1 МПа;

– определить v₄.

Для определения v₄ используем соотношение параметров изобарного процесса

4 – 1:

, , ;

г) для точки 3 дано: v₃ = v₂ = 0,246 ;

– определить p₃ и T_3.

Для определения T₃ используем уравнение политропы в T – v координатах при показателе политропы n = 1,3:

или

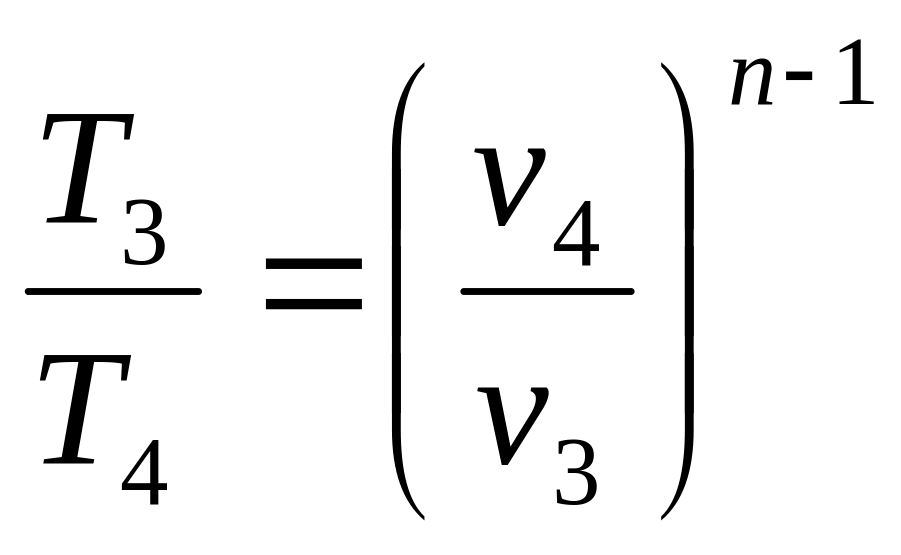
откуда

, K

Для определения p₃ используем уравнение состояния:

откуда

, Па.

Результаты расчета внести в Таблицу № 1

Таблица № 1

Параметр ® Точка ¯	P, бар	V, м3/кг	Т, К
1	1,00	0,800	273
2	5,05	0,246	433
3	5,98	0,246	513
4	1,00	0,990	338

2. Для каждого из процессов определить значения показателей политропы (n) и теплоемкости (c), вычислить изменение внутренней энергии (Du), энтальпии (Dh), энтропии (Ds), теплоту процесса (q), работу процесса (l) и располагаемую работу (l₀):

a) – процесс 1– 2 – адиабатный:

– определить показателей политропы – для адиабатного процесса:

n =

– определить теплоемкость:

; но т. к. dq = 0, то c = 0.

– вычислить изменение внутренней энергии (Du), энтальпии (Dh), энтропии (Ds):

Du_2-1 = c_v DТ = c_v (T₂ – T₁) = 0,738 (433 – 273) = 118 [кДж/кг]

Dh_2-1 = c_p DТ = c_p (T₂ – T₁) = 1,025 (433 – 273) = 164 [кДж/кг]

Ds_2-1 = 0, т.к. процесс 1– 2 – адиабатный,

q = 0 и теплообмен в нем отсутствует,

– работу процесса и располагаемую работу определить из уравнений первого закона термодинамики:

l_1-2 = q_1-2 – Du_2-1 = – Du_2-1 = – 118 [кДж/кг]

l_0,1-2 = q_1-2 – Dh_1-2 = – Dh_1-2 = – 164 [кДж/кг]

б) – процесс 2– 3 – изохорный:

– теплоемкость для изохорного процесса равна

с = с_v = 0,738 ;

– определить показателей политропы для изохорного процесса:

n = (с – c_p)/(с – с_v) = (с_v – c_p)/(с_v – с_v) = (с_v – c_p)/0 = ∞,

n = ∞,

– вычислить изменение внутренней энергии (u), энтальпии (h), энтропии (s):

u_3-2 = c_v Т = c_v (T₃ – T₂) = 0,738 (513 – 433) = 59,0 [кДж/кг]

h_3-2 = c_p Т = c_p (T₃ – T₂) = 1,025 (513 – 433) = 82 [кДж/кг]

s_3-2 = c_v ln Т₃/Т₂ = 0,738 = 0,125 [кДж/кг K]

– теплоту процесса можно определить по формуле:

q_2-3 = c Т = c_v (T₃ – T₂) = u = 59 [кДж/кг]

– где c = c_v – теплоемкость газа в рассматриваемом процессе v = const,

– работа в процессе v = const равна нулю, т.е. l_2-3 = 0:

l_2-3 = p ∆v_3-2 = 0

– располагаемую работу процесса определить из уравнений первого закона термодинамики:

так как

l_0,2-3 = q_2-3 – h_3-2 = 59 – 82 = – 23 [кДж/кг]

в) – процесс 3 – 4 – политропный:

– показатель политропы задан: n = 1,3

– теплоемкость для политропного процесса равна

c = c_v(n – k)/(n – 1) = 0,738 = – 0,221,

– вычислить изменение внутренней энергии (Du), энтальпии (Dh), энтропии (Ds):

Du_4-3 = c_v DТ = c_v (T₄ – T₃) = 0,738 (338 – 513) = – 129 [кДж/кг]

Dh_4-3 = c_p DТ = c_p (T₄ – T₃) = 1,025 (338 – 513) = – 179,4 [кДж/кг]

Ds_4-3 = c_v ln Т₄/Т₃ + R ln v₄/v₃ = 0,738 = 0,092 [кДж/кг K]

– теплоту процесса можно определить по формуле:

q_4-3 = c DТ = c (T₄ – T₃) = – 0,221(338 – 513) = 38,6 [кДж/кг]

– где c = – 0,221 – теплоемкость газа в рассматриваемом политропном процессе;

– работу в процессе определить из уравнений первого закона термодинамики:

l_4-3 = q – Du = 38,6 + 129 = 167,6 [кДж/кг]

– располагаемую работу в процессе определить из уравнений первого закона термодинамики:

l_04-3 = q – Dh = 38,6 + 179,4 = 218 [кДж/кг]

г) – процесс 4 – 1 – изобарный:

–теплоемкость для изобарного процесса равна

с = с_p = 1,025 ;

– определить показателей политропы для изобарного процесса:

n = (с–c_p)/(с–с_v) = (с_p – c_p)/(с_p–с_v) = 0/(с_p–с_v) = 0,

n = 0;

– изменение внутренней энергии и энтальпии идеального газа определить по формулам:

Du_1-4 = c_v DТ = c_v (T₁ – T₄) = 0,738 (273 –338) = – 48 [кДж/кг]

Dh_1-4 = c_p DТ = c_p (T₁ – T₄) = 1,025 (273 –338) = – 66,6 [кДж/кг]

– изменение энтропии в рассматриваемом процессе определить по одной из следующих формуле:

Ds_1-4 = c_p ln Т₁/Т₄ = 1,025 = – 0,217 [кДж/кг K]

– теплоту процессов можно определить по формуле:

q_4-1 = c DТ = c_p (T₁ – T₄) = Dh_1-4 = – 66,6 [кДж/кг]

– где c = c_p – теплоемкость газа в рассматриваемом процессе,

– работу процесса и располагаемую работу процесса определить из уравнений первого закона термодинамики:

l_1-4 = q_4-1 – Du_1-4 = – 66,6 + 48 = – 18,6 [кДж/кг]

l_01-4 = q_4-1 – Dh_1-4 = – 66,6 + 66,6 = 0 [кДж/кг]

Все величины, найденные в данном пункте, внести в таблицу 2 с указанием знаков, полученных в расчете.

В таблицу 2 необходимо включить итоговую строчку по вертикальным графам, содержащим величины: Du, Dh, Ds, q, l, l₀.

Для величин Du, Dh и Ds суммы должны быть равны нулю, так как u, h и s - функции состояния и, следовательно, за цикл их изменение равно нулю. Суммы q, l и l₀ должны быть равны между собой и обязательно положительны (цикл прямой):

åq = ål = ål₀ [кДж/кг]

Графы, содержащие показатели процессов и теплоемкости суммированию не подлежат.

Таблица №2

Параметр→ Процесс ↓	n	c, кДж/кг*К	∆u, кДж/кг	∆h, кДж/кг	∆S, кДж/кг*К	q, кДж/кг	l, кДж/кг	l0, кДж/кг
1–2	1,39	0,000	118	164	0,000	0,000	-118	-164
2–3	∞	0,738	59	82	0,125	59	0	- 23
3–4	1,3	– 0,221	-129	-179,4	0,092	38,6	167,6	218
4–1	0	1,025	- 48	- 66,6	-0,217	-66,6	-18,6	0
Σ	–	–	0,000	0,000	0,000	31,0	31,0	31,0

3. Определить суммарные количества подведенной (q') и отведенной (q'') теплоты, работу цикла (l_ц), располагаемую работу цикла (l_0ц) и термический к.п.д. цикла (h_t).

– количество подведенной теплоты:

q' = åq_{i положит.} = q_1-2 + q_2-3 + q_3-4 = 0 + 59 + 38,6 = 97,6 [кДж/кг]

– количество отведенной теплоты:

q" = åq_{i отрицат.} = q_4-1 = – 66,6 [кДж/кг]

– количество теплоты, полученное системой за цикл:

q_ц = åq_i = q_1-2 + q_2-3 + q_3-4 + q_4-1 = 0 + 59 + 38,6 – 66,6 = 31,0 [кДж/кг]

– определить работу цикла:

l_ц = ål_i = l_1-2 + l_2-3 + l_3-4 + l_4-1 = –118 + 0 + 167,6 – 18,6 = 31,0 [кДж/кг]

– определить располагаемую работу цикла:

l_0ц = ål_0i = l_0,1-2 + l_0,2-3 + l_0,3-4 + l_0,4-1 = – 164 – 23 + 218 + 0 = 31,0 [кДж/кг]

– определить термический к. п. д. цикла:

h_t = l_ц/q' = q_ц/ q' = (q' – |q"|)/q' = = 0,317

Полученные данные внести в таблицу №3 или представить в следующем виде:

– количество подведенной теплоты:

q' = 97,6 [кДж/кг]

– количество отведенной теплоты:

q" = – 66,6 [кДж/кг]

– количество теплоты, полученное системой за цикл:

q_ц = 31,0 [кДж/кг]

– работа за цикл:

l_ц = 31,0 [кДж/кг]

– располагаемая работа за цикл:

l_0ц = 31,0 [кДж/кг]

– термический к. п. д. цикла:

h_t = 0,317

4. Построение цикла. Рассматриваемый цикл должен быть построен в масштабе в системе координат: lg v–lg p, v–p и s–Т.

а) в координатах lg v – lg p – цикл представлен на рис. 2. Цикл строится на логарифмической бумаге или в логарифмических координатах при этом не требуется определять логарифмы. При отсутствии логарифмической бумаги построение выполняется на миллиметровой бумаге (в этом случае требуется определять логарифмы). Проследить, чтобы одноименные процессы в координатах lg v–lg p изображались параллельными линиями. Если этого нет, необходимо проверить правильность определения параметров основных точек цикла. Цель данного построения – получить значения p и v в промежуточных точках в политропном, адиабатном и изотермическом процессах, если они есть в цикле, для выполнения следующего пункта.

В данном задании процессы: адиабатный 1– 2 и политропный 3 – 4 изображаются прямыми линиями (рис. 2), поэтому для любого промежуточного давления в этих процессах можно графически определить соответствующий удельный объем.

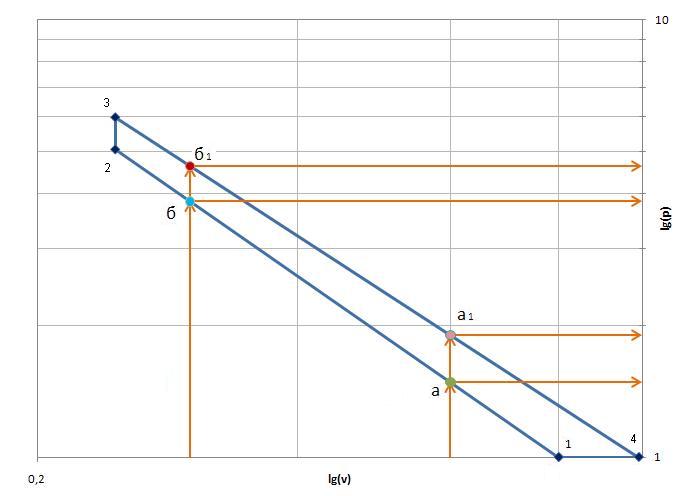
Рис. 2

Значения промежуточных точек сводятся в таблицу № 3:

адиабатный 1– 2, промежуточные точки – а и б

политропный 3 – 4, промежуточные точки – а₁ и б₁

Таблица № 3

Параметр  Точка 	V, м3/кг	P, бар
а	0,6	1,48
б	0,3	3,85
а1	0,6	1,90
б1	0,3	4,63

б) в координатах p–v;

задаться масштабом

в 1 1

в 1 0,02

– диаграмма цикла строится в обычной равномерной шкале в координатах v–p для процессов, изображаемых кривыми линиями, строится по данным таблиц №1 и №3, из которых берутся значения p и v для двух–трех промежуточных точек для каждого процесса. Диаграмму рекомендуется строить на листе миллиметровой бумаги, в таком масштабе, чтобы цикл на диаграмме получился размером порядка 100 х 100 мм (Рис. 3).

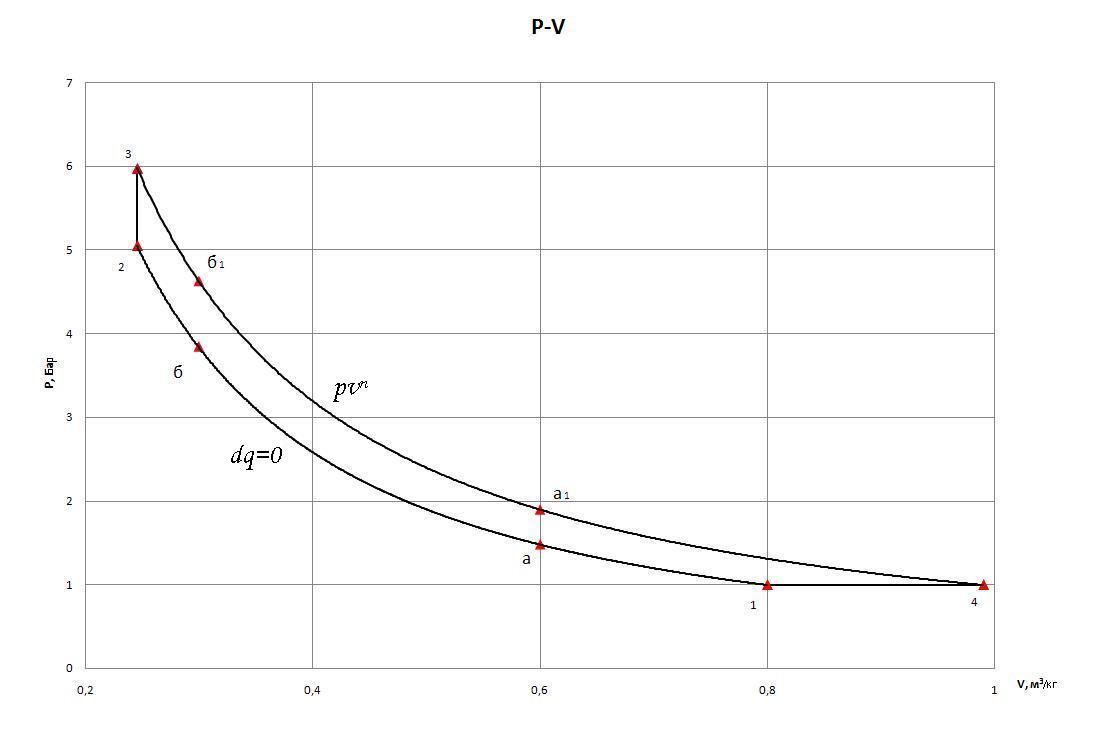
Рис. 3

в) в координатах ;

задаться масштабом

в 1 20 ,

в 1 0,016 ;

– для построения диаграммы цикла в координатах s–Т используются параметры, подсчитанные в пунктах 1 (Т) и 2 (s), кривые процессов можно заменить прямыми линиями. На диаграмме должен быть показан порядок построения.

Задается масштаб температуры _T и масштаб энтропии _s, на оси температур (ординат) наносится шкала, на оси энтропий (абсцисс) шкала не наносится. Начало построения на оси энтропий выбирается произвольно (см. рис.4): если s > 0 (см. табл. 2), то начало построения можно сместить к оси ординат, т.к. процесс пойдет вправо; если s < 0 (см. табл. 2), то начало построения следует сместить вправо, т.к. процесс пойдет влево.

– таким образом, выбрав произвольно начало построения цикла, восстанавливаем перпендикуляр к оси энтропий и проводим его до пересечения с температурой вначале цикла (процесса) Т₁ – это будет точка 1 – точка начала цикла и процесса 1 – 2.

– откладываем от проекции точки 1 на оси энтропий значение изменения энтропии s_1-2 в процессе 1 - 2 (см. табл. 2), если s > 0, то откладываем вправо, если s_1-2 < 0, то откладываем влево и из полученной точки восстанавливаем перпендикуляр до пересечения с температурой в конце процесса Т₂ - точка пересечения дает точку 2.

– соединяем точки 1 и 2 - процесс построен. Аналогично строятся все процессы цикла.

5. Для одного из процессов цикла (кроме изотермического) построить схему графического нахождения u, h, q. На данную схему следует нанести численные значения необходимых для подсчета величин. На схеме приводятся абсолютные температуры в начале и конце процесса, изменение энтропии в процессе (для определения q) и изменения энтропии s_v и s_p (для определения u и h). Необходимо разобраться в площадях, соответствующих всем определенным величинам. При графическом исследовании процессов в диаграмме для простоты их заменяют прямыми линиями (Рис. 4).

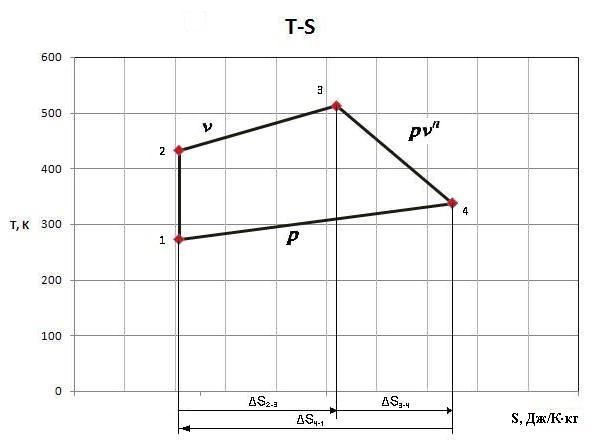
Рис. 4

Для лучшего уяснения графического решения рассмотрим примеры построения всех процессов рассматриваемого цикла.:

1. – на рис. 5 приведен в диаграмме процесс 1– 2 – адиабатный:

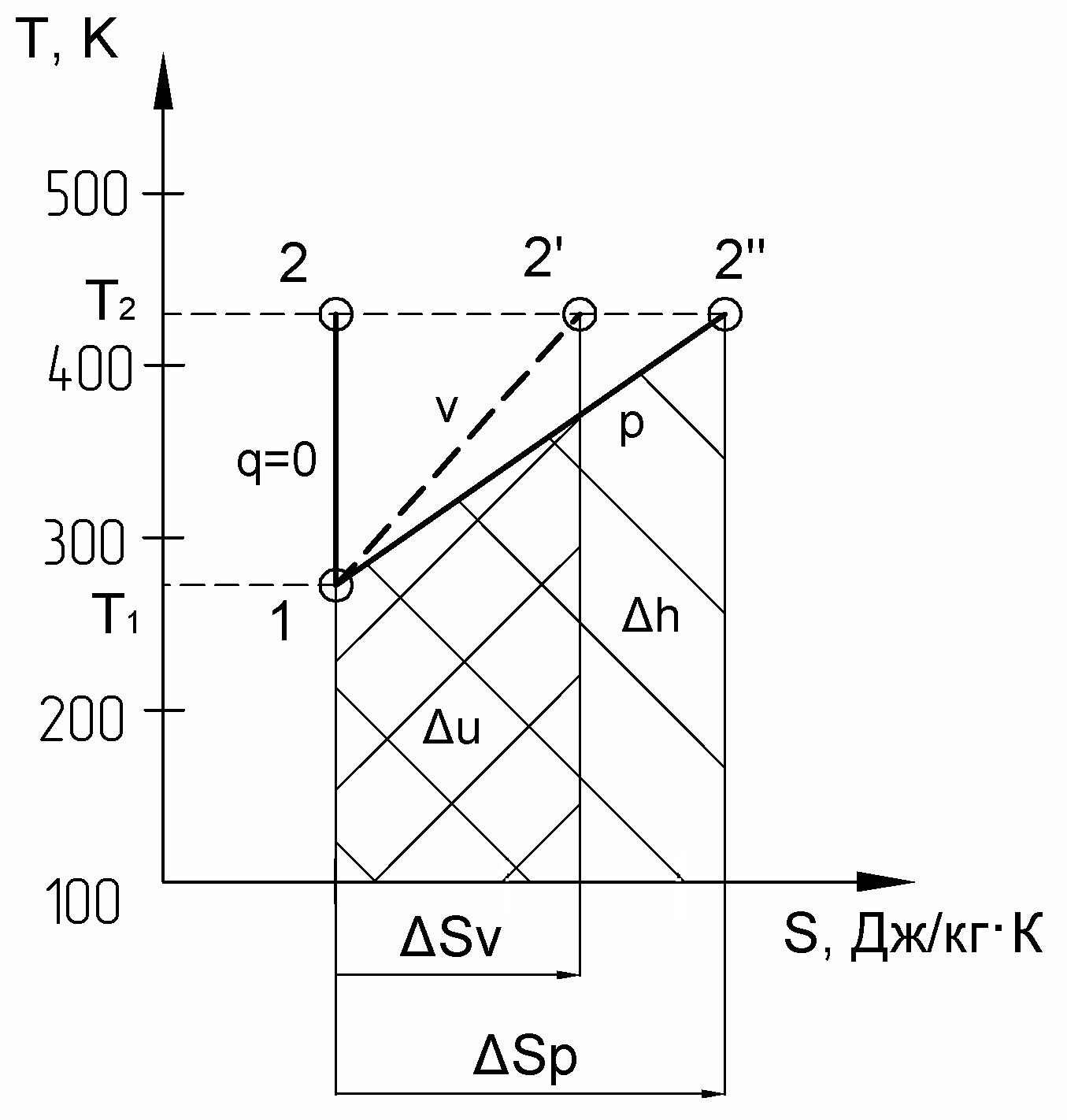
Рис. 5

– площадь под адиабатой равна нулю, т.к. q = 0;

– площадь под изохорой, проведенной в данном интервале температур, численно равна изменению внутренней энергии в процессе 1– 2:

u = u₂ – u₁ = пл. а12^б = s_v 0,5(T₁ + T₂) = 0,340 0,5 (273 +433) = 120 [кДж/кг],

где s_v = c_v ln (Т₂/Т₁) = 0,738 ln (433/273) = 0,340 [кДж/кг K],

т.к. s_v > 0, то его численное значение откладывается в масштабе от точки а вправо и получаем точку б, из которой восстанавливается перпендикуляр до пересечения с температурой в конце процесса в точке 2, соединяя точки 1 и 2 получаем изохору 1– 2.

– площадь под изобарой, проведенной в данном интервале температур, численно равна изменению энтальпии в процессе 1– 2:

h = h₂ – h₁ = пл. а12^в = s_p 0,5(T₁ + T₂) = 0,473 0,5 (273 +433) = 167 [кДж/кг],

где s_p = c_p ln (Т₂/Т₁) = 1,025 ln (433/273) = 0,473 [кДж/кг K],

т.к. s_p > 0, то его численное значение откладывается в масштабе от точки а вправо и получаем точку в, из которой восстанавливается перпендикуляр до пересечения с температурой в конце процесса в точке 2, соединяя точки 1 и 2 получаем изобару 1– 2.

б) – на рис. 6 приведен в диаграмме процесс 2 – 3 –изохорный:

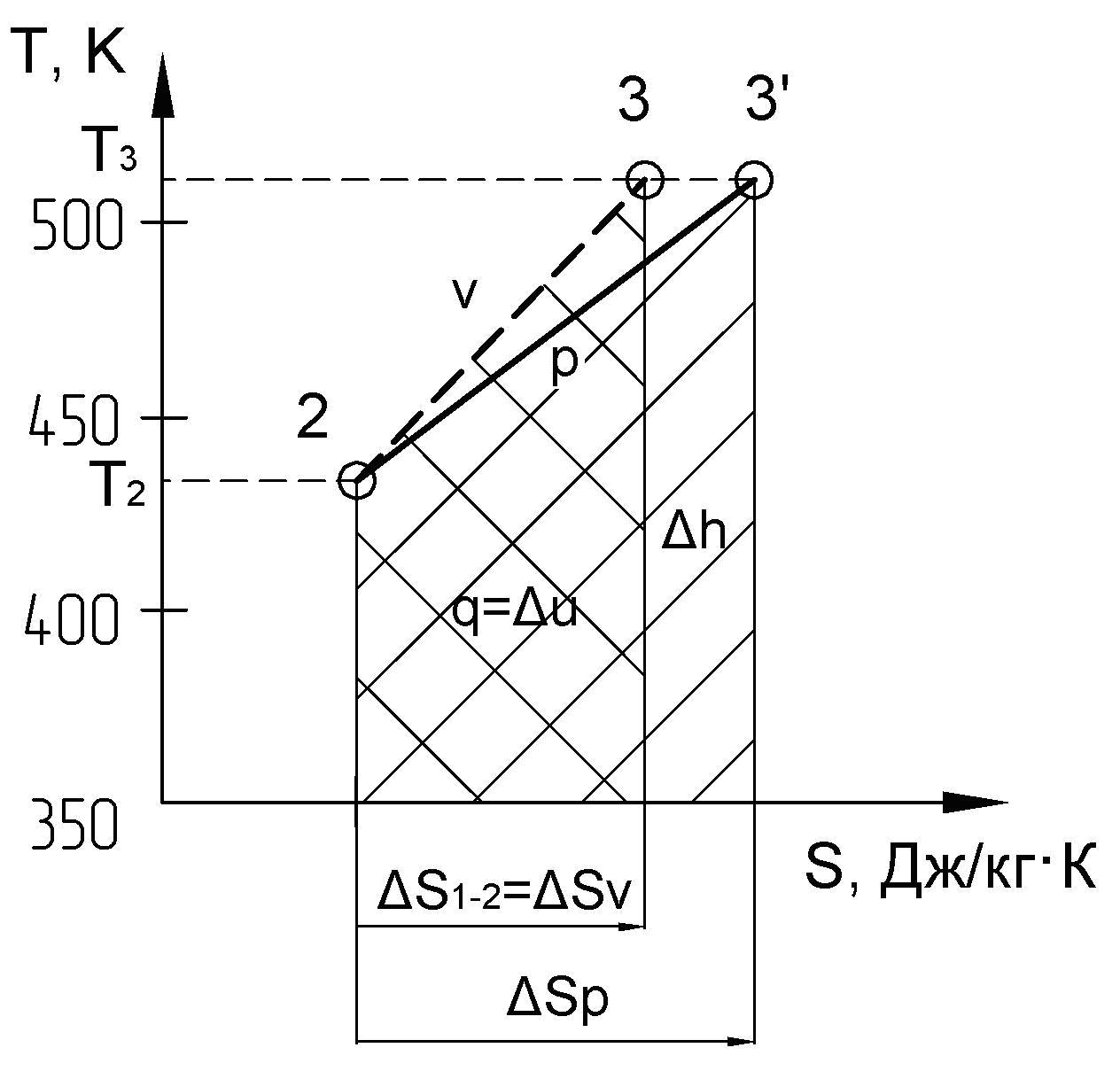
Рис. 6

– площадь под изохорой пл. а23б равна количеству теплоты, подведенной в процессе 2 – 3 и численно равна изменению внутренней энергии в этом процессе v = const:

где из таблицы №2 имеем s_v = 0,125 [кДж/кг K]:

q = u = u₃ – u₂ = пл. а23б = s_v 0,5(T₂ + T₃) = 0,125 0,5 (433 + 513) = 59 [кДж/кг],

т.к. s_v > 0, то его численное значение откладывается в масштабе от точки а вправо и получаем точку б, из которой восстанавливается перпендикуляр до пересечения с температурой в конце процесса в точке 3 (см. пункт 4), соединяя точки 2 и 3 получаем изохору 2 – 3.

– площадь под изобарой пл. а23в, проведенной в данном интервале температур, численно равна изменению энтальпии в процессе 2 – 3:

h = h₃ – h₂ = пл. а23в = s_p 0,5(T₂ + T₃) = 0,174 0,5 (433 +513) = 82,3 [кДж/кг],

где s_p = c_p ln (Т₃/Т₂) = 1,025 ln (513/433) = 0,174 [кДж/кг K],

т.к. s_p > 0, то его численное значение откладывается в масштабе от точки а вправо и получаем точку в, из которой восстанавливается перпендикуляр до пересечения с температурой в конце процесса в точке 3, соединяя точки 1 и 3 получаем изобару 2 – 3.

в) – на рис. 7 приведен в диаграмме процесс 3 – 4 – политропный:

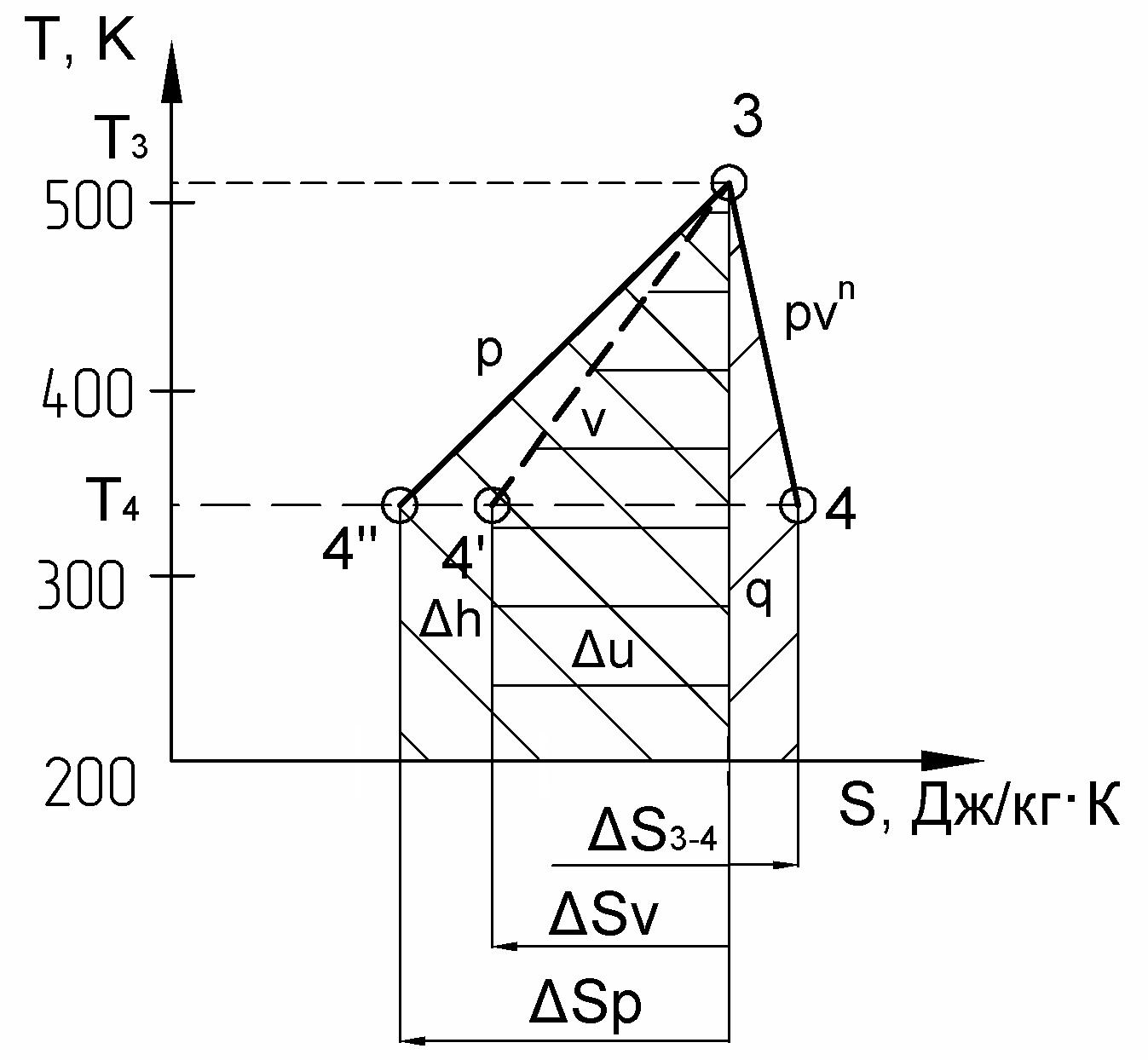
Рис. 7

– площадь под политропой пл. а34б равна количеству теплоты, подведенной в процессе 3 – 4:

где из таблицы №2 имеем s_3-4 = 0,092 [кДж/кг K]:

q = пл. а34б = s_3-4 0,5(T₃ + T₄) = 0,092 0,5 (513 + 338) = 39,14 [кДж/кг]:

u = u₄ – u₃ = пл. а34в = s_v 0,5(T₃ + T₄) = – 0,308 0,5 (513 + 338) = – 131 [кДж/кг],

где s_v = c_v ln (Т₄/Т₃) = 0,738 ln (338/513) = – 0,308 [кДж/кг K],

т.к. s_v < 0, то его численное значение откладывается в масштабе от точки а влево и получаем точку в, из которой восстанавливается перпендикуляр до пересечения с температурой в конце процесса в точке 4, соединяя точки 3 и 4 получаем изохору 3 – 4.

– площадь под изобарой пл. а34с, проведенной в данном интервале температур, численно равна изменению энтальпии в процессе 3 – 4:

h = h₃ – h₂ = пл. а34с = s_p 0,5(T₂ + T₃) = – 0,428 0,5 (513 +338) = –182,1 [кДж/кг],

где s_p = c_p ln (Т₄/Т₃) = 1,025 ln (338/513) = – 0,428 [кДж/кг K],

т.к. s_p < 0, то его численное значение откладывается в масштабе от точки а влево и получаем точку с, из которой восстанавливается перпендикуляр до пересечения с температурой в конце процесса в точке 4, соединяя точки 3 и 4 получаем изохору 3 – 4,

г) – на рис. 8 приведен в диаграмме процесс 4 – 1 –изобарный:

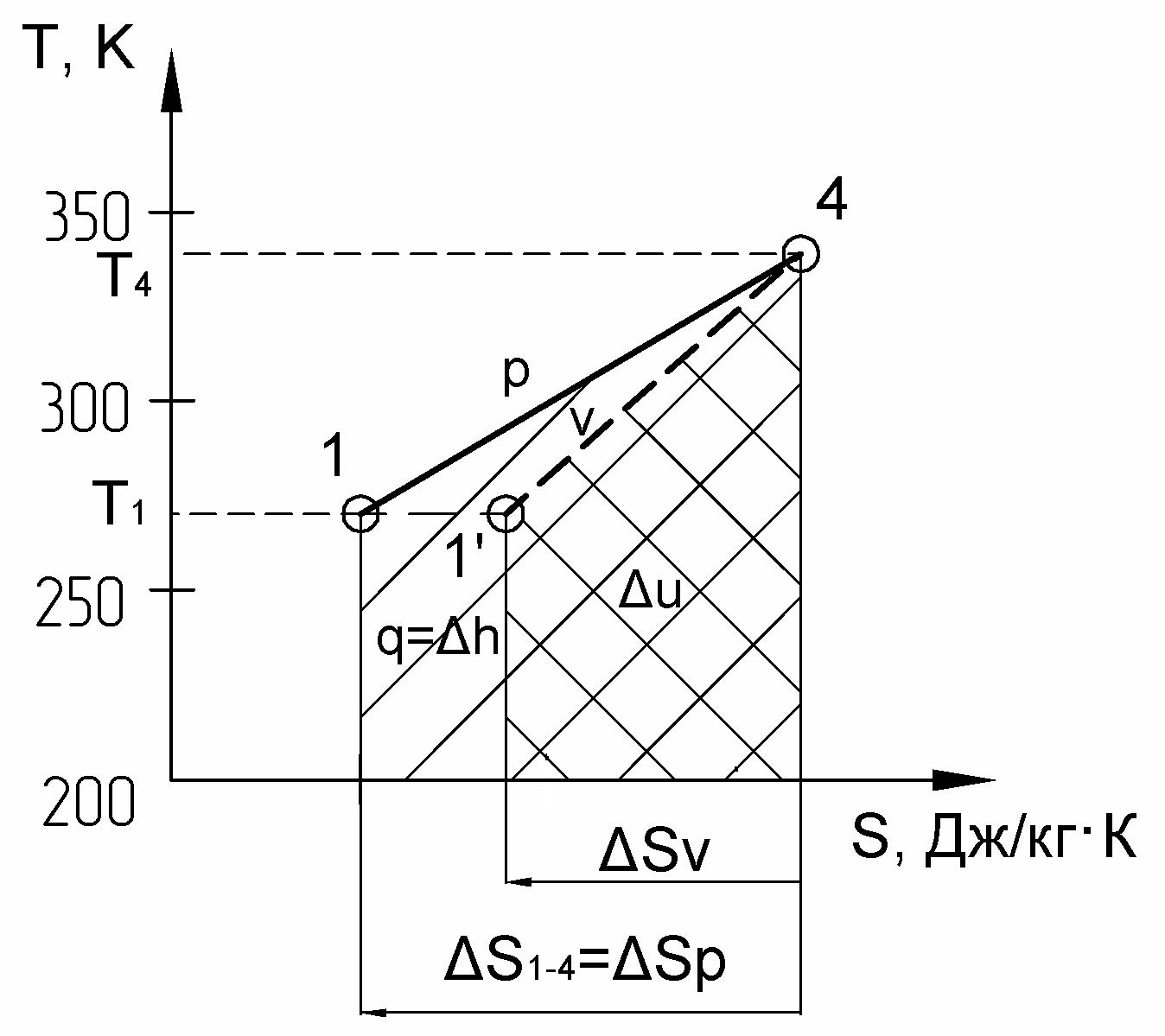
Рис. 8

– площадь под изобарой пл. а41б равна количеству теплоты, подведенной в процессе 4 – 1 и численно равна изменению энтальпии в этом процессе p = const:

где из таблицы №2 имеем s_p = – 0,21 [кДж/кг K]:

q = h = h₁ – h₄ = пл. а41б = s_p 0,5(T₁ + T₄) = – 0,21 0,5 (338 + 273) = - 64,2 [кДж/кг],

т.к. s_p  0, то его численное значение откладывается в масштабе от точки а влево и получаем точку б, из которой восстанавливается перпендикуляр до пересечения с температурой в конце процесса в точке 1 (см. пункт 4), соединяя точки 4 и 1 получаем изобару 4 – 1.

– площадь под изохорой пл. а41в, проведенной в данном интервале температур, численно равна изменению внутренней энергии в процессе 4 – 1:

u = u₁ – u₄ = пл. а41в = s_v 0,5(T₄ + T₁) = – 0,158 0,5 (338 + 273) = – 48,2 [кДж/кг],

где s_v = c_v ln (Т₁/Т₄) = 0,738 ln (273/338) = – 0,158 [кДж/кг K],

т.к. s_v  0, то его численное значение откладывается в масштабе от точки а влево и получаем точку в, из которой восстанавливается перпендикуляр до пересечения с температурой в конце процесса в точке 1, соединяя точки 4 и 1 получаем изобару 4 – 1.