3.1 Планирование полного факторного эксперимента

Математическое описание функции отклика моделируемой системы в окрестности точки базового (нулевого) уровня (х₁₀, х₂₀), можно получить варьированием каждого из факторов x_j на двух уровнях, отличающихся от базового (нулевого) уровня х_{j 0} на величину интервала варьирования х_j.

Базовый уровень выбирают в середине диапазона

х_{j 0} =0,5(x_jmin+ x_jmax).

Интервалы варьирования по каждому фактору могут быть различными. Их выбирают равными 10-60% от рассматриваемого диапазона:

х_j=(0,1 – 0,6) (x_{j max} – x_{j min}),

тo есть так, чтобы приращение отклика можно было выделить на фоне "шума" (действия случайных факторов) при небольшом числе параллельных опытов.

Таким образом, находят верхний и нижний уровни факторов, при которых будет проводиться эксперимент:

x_jв = x_{j 0} + х_j , x_jн = x_{j 0} – х_j . (1)

Такая запись не всегда является удобной, и поэтому при планировании эксперимента для простоты записи и удоб­ства обработки экспериментальных данных преобразуют значения факторов в безразмерные, кодированные величины по следующему правилу:

,

После такого преобразования при значение

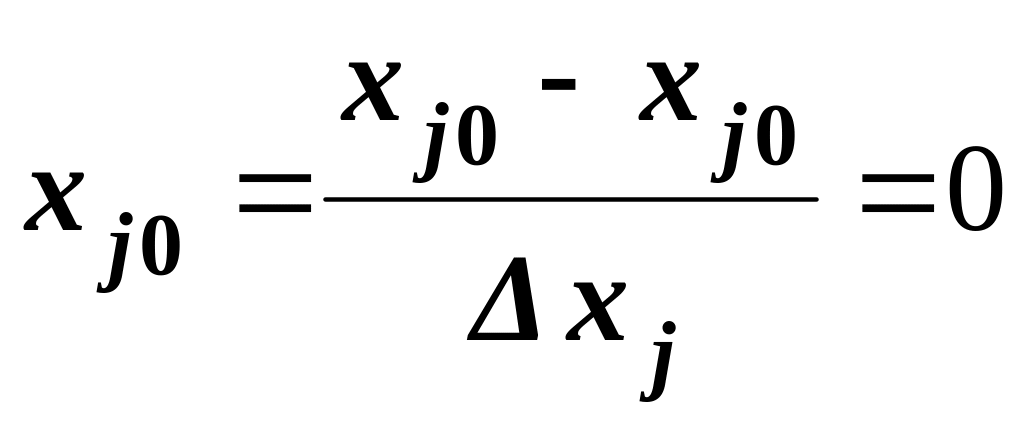, а значения x_jв и x_jн с учётом (1) соответственно равны +1 и –1.

Приведем табл. 1 планирования эксперимента для случая одной характеристики y и двух факторов x_1, x₂, когда математическая модель (уравнение регрессии) содержит члены со степенью переменных, не превышающей единицу:

y = b₀ x₀+ b₁ x₁+ b₂ x₂+ b₁₂ x₁x₂. (2)

Таблица 1

№ опыта	Матрица планирования				Значение y
	x0	План эксперимента (комбинации влияющих факторов)		x1x2
		x1	x2
1	1	– 1	– 1	+ 1	y1
2	1	+ 1	– 1	– 1	y2
3	1	– 1	+ 1	– 1	y3
4	1	+ 1	+ 1	+ 1	y4

Число комбинаций значений x₁ и x₂ в этом случае равно 4. Целью построения таблицы является разработка плана проведения эксперимента для определения оценок b₀, b₁, b₂, b₁₂ – коэффициентов (параметров) уравнения регрессии.

Для оценки свободного члена b₀ (ожидаемого значения характеристики в центре плана) и определения эффекта взаимодействия факторов x₁ и x₂ в табл. 1 план экспе­римента расширяется до матрицы планирования.

Расшире­ние плана эксперимента осуществляется путём добавления столбца "фиктивной" переменной x₀=+1 и столбца произве­дения x₁x₂. Матрица планирования, составленная подобным образом, существенно упрощает процедуру вычисления оценок коэффициентов уравнения регрессии.

Вследствие того, что изменение характеристики y носит случайный характер для каждой комбинации значений фак­торов необходимо проводить несколько опытов, называе­мых параллельными, результаты которых осредняются.