2.7. Мощность, переносимая модой по диэлектрическому планарному волноводу.

2.7.1. Переносимая мощность. Выражения для полей, направляемых пленкой Н- и Е-мод (2.17), (2.20) позволяют определить среднюю мощность, переносимую отдельной модой вдоль оси Z на единичную ширину в направлении Y (см. рис. 2.1,б).

Задание: получить последовательно (2.47) – (2.50).

В частности для Н-мод с учетом (2.6,а)

(2.47)

где – комплексный вектор Пойнтинга; ( единичный орт оси Z ).

Подставляя в (2.34) выражения для из (2.17), находим

(2.48)

Для Е- мод с учетом (2.6)

(2.49)

Подставляя в (2.49) выражение для из (2.20), находим

. (2.50)

2.7.2. Соотношения ортогональности направляемых мод. Учитывая (2.47), (2.49) можно показать, что для Н-мод имеет место соотношение

, (2.51)

где – индексы двух различных мод; – символ Кронекера, который равен нулю для и единице для .

Из (2.51) следует, что при левая часть равна мощности, переносимой вдоль пленочного волновода (с единичной шириной вдоль направления Y) модой ; при правая часть равна нулю. Физическая суть этого в том, что различные моды в процессе распространения не обмениваются энергией (не взаимодействуют).

Соответственно для Е-мод

. (2.52)

Соотношение (2.51), (2.52) представляют собой так называемые соотношения ортогональности между двумя модами в диэлектрическом волноводе без потерь.

Задание: получить (2.51) или (2.52).

2.8. Затухание в диэлектрическом волноводе.

Анализ Н- и Е-мод в планарном диэлектрическом волноводе проводился в предположении, что диэлектрик является идеальным (без потерь). При этом в режиме направляемых поверхностных мод (волноводных мод), определяемом условием (2.28), коэффициент распространения – действительная величина. Наличие диэлектрических или магнитных потерь в материале диэлектрического волновода (подложки, покрытия) вызовет преобразование части электромагнитной энергии, переносимой волной, в тепловую энергию. Можно предположить, что для планарного диэлектрического волновода с потерями за счет конечной проводимости диэлектрических сред зависимость полей от координаты Z имеет формально тот же вид, что и для случая без потерь (2.4). Однако при этом является комплексной величиной: . Поэтому любая составляющая поля в соответствии с (2.4) будет изменяться по закону , где – величина, характеризующая убывание произвольной составляющей электромагнитной волны вдоль оси Z ( –коэффициент затухания, –коэффициент фазы).

Так как средняя мощность Р (2.48), (2.50) пропорциональна квадрату амплитуды поля, то , где Р₀ – средняя за период мощность в сечении z=0 диэлектрического волновода.

Разность между мощностями в сечении z и равна мощности потерь на отрезке волновода длиной : . Разделив обе части равенства на и устремив к нулю, найдем значение мощности тепловых потерь, приходящееся на единицу длины:

, откуда , (2.53)

где – коэффициент затухания, 1/м.

Мощность Р, переносимая вдоль планарного диэлектрического волновода с Н- и Е-модами, определяется соотношениями (2.47) – (2.49). Средняя за период мощность тепловых потерь находится из выражения

, (2.54)

где интегрирование ведется по всему объему, заполненному диэлектриком с потерями, при единичной длине в направлении Y, при этом в зависимости от области подставляется соответствующее значение (i=1,2,3).

Задание: пояснить формулу (2.54), используя уравнение баланса для средней за период мощности (см. например, [3], [4]).

В заключение отметим следующие три обстоятельства. Во-первых, поскольку определяется отношением к мощности Р, переносимой вдоль планарного диэлектрического волновода, то интегрирование выражений (2.49), (2.50), (2.54) по переменной y можно производить не в бесконечных пределах, а по отрезку единичной длины. Во-вторых, при вычислении и Р предполагается, что структура Н- и Е-мод в диэлектрическом волноводе приблизительно совпадает со структурой этих волн в среде без потерь. В-третьих, если исследуется диэлектрическая пластина на металлический подложке (см. рис.2.17), то необходимо учитывать среднюю мощность тепловых потерь в металле, которая рассчитывается аналогично случаю металлических волноводов:

, (2.55)

где – касательная составляющая магнитного поля на металлической поверхности; – удельное поверхностное сопротивление металла, Ом ( - проводимость металла). Подставляя в формулу (2.47), (2.49), (2.54) выражения для соответствующих компонент Н- или Е-мод (2.17), (2.20) или (2.29), находим выражение для коэффициента затухания (2.53) в диэлектрическом планарном волноводе. Очевидно, что при конкретных расчетах необходимо сначала определить волновые числа h, p, q (р, h) с помощью численных методов (см. разд.3).

2.9. H-образный металлодиэлектри-ческий волновод.

H-образнная металлодиэлектрическая линия передачи рис. 2.8 представляет собой диэлектрическую пластину, ограниченную с двух сторон металлическими плоскостями. Здесь поле должно удовлетворять граничным условиям на поверхностях металлических пластин:

(2.56)

а также граничным условиям условиям для H- или E-волн на границах x=a и x=-a (см.параграф 2.2, 2.3).

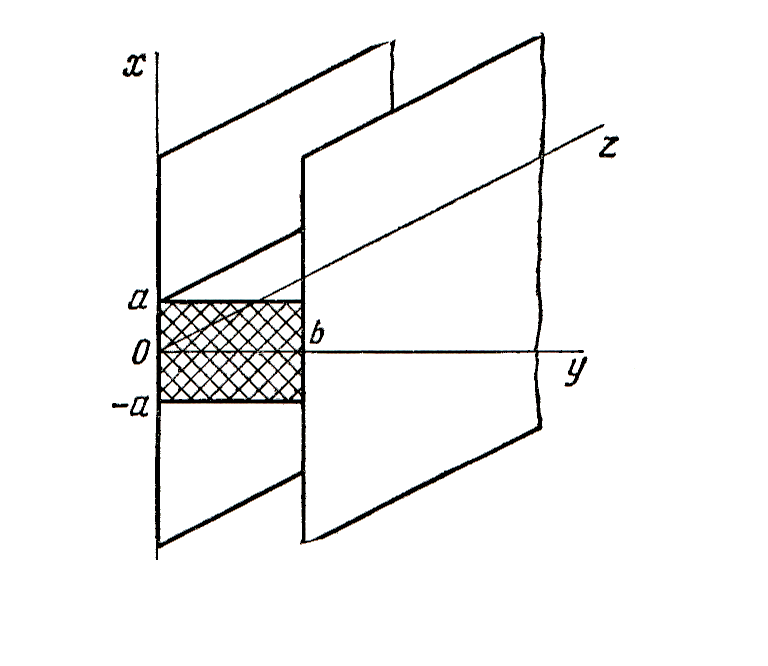
Рис.2.8. Н-образный металлодиэлектрический волновод

Из волн типа E в такой структуре могут существовать только чётные волны, а из волн типа H – только нечётные.

Основной волной H-образной линии передачи является волна магнитного типа H₁₀, вектор которой имеет единственную составляющую, причём все составляющие векторов поля не зависят от координаты y. Эта волна полностью аналогична основной волне магнитного типа диэлектрической пластины; в частности, она имеет такую же фазовую скорость, как и волна типа H₁ диэлектрической пластины.

Все остальные типы волн H-образнной линии передачи имеют одну или несколько вариаций вдоль оси y. Характеристические уравнения для этих типов волн оказываются более сложными.

Задание: провести по аналогии с разделами 2.1, 2.2 все рассуждения для H-волн в H-образной линии передачи.

3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИСПЕРСИОННОГО УРАВНЕНИЯ.

3.1. Вводные замечания.

В разд.2.4 дисперсионное уравнение (2.23) решается графически. Конечным результатом решения является дисперсионная характеристика (см. рис. 2.4,б), представляющая собой зависимость нормированной постоянной распространения для Е - и Н-мод от относительной толщины пленки . Графический способ прост, нагляден, однако обладает невысокой точностью и поэтому применяется редко.

Универсальными способами решений дисперсионных уравнений (2.26), (2.27), (2.32а)-(2.32г) являются численные методы решений нелинейных уравнений такого типа [10]. Ниже приводятся два метода: “половинного деления” (дихотомии) и аппроксимации. Алгоритм “половинного деления” является универсальным. Он позволяет получать решение с заданной точностью независимо от сложности дисперсионного уравнения, однако обладает медленной сходимостью. При сложном виде дисперсионного уравнения для повышения скорости вычислений целесообразно применить более быстро сходящиеся методы, в частности простой и наглядный метод аппроксимации.

Для численного решения рассмотренные выше характеристические уравнения в (2.17), (2.19) для Е - и Н-мод асимметричного волновода представим в виде

(3.1)

где для Н-мод , а для Е-мод ,1,2… – индекс моды.

В уравнении (3.1) следует брать главные значения арктангенсов. Дополнительные условия связи между коэффициентами h,p,q представим в виде (см.(2.19))

(3.2)

Подставляя уравнения (3.2) в (3.1) и отделяя линейную и нелинейную части, получим

, (3.3)

где

(3.4)

Уравнение (3.3) является нелинейным трансцендентным уравнением относительно параметра ; введенный параметр К характеризует степень асимметрии диэлектрического волновода.

Исходными данными при решении дисперсионного уравнения (3.3) являются длина волны , толщина волновода t, относительные диэлектрические проницаемости подложки, волноведущего слоя и покрытия соответственно (можно задавать и показатели преломления ), тип волны (Е или Н) и индекс m моды.

Определив из (3.3) параметр как искомое решение, находят далее величину , а затем из (2.25) – постоянную распространения и поперечные волновые числа p и q, что позволяет построить дисперсионную кривую (см. рис.2.4,б) и определить структуру соответствующей волны по формулам (2.17), (2.20).

В случае направляемых поверхностных волн коэффициенты h, p, q – положительные действительные числа. В соответствии с (3.2), (3.4) значение безразмерного параметра находятся в пределах

. (3.5)

3.2. Метод “половинного деления”.

В соответствии с (3.3) введем функцию :

. (3.6)

3.2.1. Алгоритм решения. Решением уравнения (3.3) являются такие значения , при которых функция . Поскольку в общем случае неизвестно, имеются ли такие решения на интервале [0,1], то более целесообразно искать не нуль функции , а некоторый малый интервал , в котором меняет знак. Такой интервал всегда можно найти, а затем сузить его настолько, чтобы выполнялось условие , где – заданная точность решения.

На рисунке 3.1 для иллюстрации метода представлена некоторая функция в интервале . При заданной точности определение корня алгоритма состоит из следующих шагов:

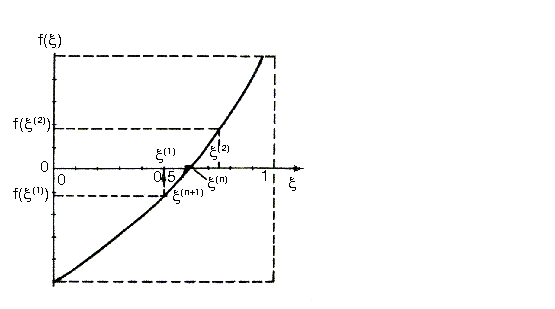
Рис. 3.1. К решению трансцендентного уравнения методом половинного деления.

1. Проверяют наличие корня уравнения (3.6) в заданном интервале. Если , то корней уравнения (3.6) нет, т.е. при выбранных исходных данных, заданном типе волны и индексе m моды волна в диэлектрическом волноводе не распространяется.

2. Меняя параметр m (номер моды), удовлетворяют условию .

3. Определяют “корень” на этапе первой итерации по формуле

(3.7)

и вычисляют

4. Проверяют условия: если , то сужают интервал поиска корня в пределах и определяют новый корень на втором этапе итерации, используя (3.7). Если же , то значение корня лежит в интервале .

5. Итерационная процедура последовательно повторяется n раз до выполнения условия . При этом значение корня рассчитывается по формуле

. (3.8)

Данный алгоритм позволяет вычислить значение с гарантированной точностью .

3.2.2. Программная реализация алгоритма по методу "половинного деления" (дихотомии) на алгоритмическом языке Фортран-90*⁾

Программа "beta1" предназначена для расчета поперечных волновых чисел h в волноведущем диэлектрическом слое для Н-волн планарного однородного изотропного диэлектрического волновода. Входными данными являются: alambda – длина волны ; t – толщина волноведущего слоя; e1 – относительная диэлектрическая проницаемость покрытия; e2 – относительная диэлектрическая проницаемость волноведущего диэлектрического слоя; e3 – относительная диэлектрическая проницаемость подложки; m – номер моды. Программа определяет значение корня с заданной точностью eps. Выходной величиной является значение поперечного волнового числа h. Размерности метрических переменных следует брать одинаковыми.

!--------------------------------------------------------------

!Программа расчета волнового числа h в волноводном

!диэлектрическом слое для H-волн планарного однородного

!изотропного диэлектрического волновода

program beta1

!переменный, общие для beta1 и функции f

common /cblock/ a,ak,m

!входные данные; при указанных значениях

!результат для контроля: h = 0.8956242

!длина волны; размерности alambda и t одинаковые

alambda = 0.85

!толщина волноведущего слоя

t = 5.

!отн. диэл. проницаемость покрытия

e1 = 2.11

!отн. диэл. проницаемость волноведущего слоя

e2 = 2.14

!отн. диэл. проницаемость подложки

e3 = 2.12

!номер моды

m = 1

!погрешность значения корня

eps = 1e-6

!вычисляется коэффициент A

a = 2 * sqrt(e2-e3) * t/alambda

!вычисляется коэффициент K

ak = (e2-e1) / (e2-e3)

!обращение к функции решения уравнения F(x)=0

aksi = dih(1e-10,1.,eps)

!определение h

h = aksi * 2*3.14159/alambda * sqrt(e2-e3)

!вывод результата

print *, h

end

!--------------------------------------------------------------

!Функция решения уравнения F(x)=0 методом дихотомии

!с точностью eps при условии, что корень лежит в

!интервале от a до b

function dih(a,b,eps)

!цикл, пока не достигнута требуемая точность

do while((b-a) .gt. eps)

!c = середина отрезка [a,b]

c=(a+b)/2

!проверка знака функции в середине отрезка [a,b]

if(f(c) .gt. 0) then

!обновление правой границы если F(c) > 0

b=c

else

!обновление левой границы если F(c) = 0

a=c

endif

enddo

!dih -- решение; F(dih) = 0 с точностью до eps

dih=(a+b)/2

return

end

!--------------------------------------------------------------

!Функция F(x) для функции dih

function f(x)

!переменные, получаемые из beta1

common /cblock/ a,ak,m

f1 = atan( sqrt(1/x**2-1) )

f1 = (f1 + atan(sqrt(ak/x**2-1))) / 3.14159

f = a*x - m - f1

return

end

!--------------------------------------------------------------