Задача оптимизации временной структуры проекта.

Постановка задачи (вербальной модели): имеется проект, состоящий из nработ, t_i– время необходимое для выполнения i-ой работы. Предполагается, что всех ресурсов достаточно, чтобы начать все работы одновременно, но работы не являются независимыми, то есть имеются начальные, промежуточные (выполняются только после завершения каких-то других работ) и конечные.

Требуется определить минимальное время, за которое может быть выполнен весь проект, а также составить календарный план-график выполнения работ.

Введем множество I_i⁺ – множество работ, которые непосредственно предшествуют i-ой работе (у начальных работ I_i⁺ = )

Построим математическую модель:

Будем формировать математическую модель так, чтобы для каждой работы, все работы, которые ей предшествуют, имели более ранние номера. Разобьем все работы на три множества:

- N₁ – множество начальных работ;

- N₂–множество промежуточных работ;

- N₃–завершающие.

Введем после N₁, N₂, N₃ I_i⁺ – множество работ, введем переменные τ_i – момент раннего начала i-ой работы.

Тогда очевидно, что τ_i = 0.

Если взять N₂ и N₃ вместе, то

(3.13)

Т – время выполнения всего проекта, проект завершен тогда, когда завершены все работы.

Введем n + 1работу, у которой I⁺_n+1 = N₃ – все завершающие работы и

t_n+1 = 0.

Получим окончательный вид модели:

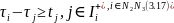
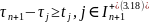
(3.19)

Модель (3.16) – (3.19) является задачей двойственной к задаче о критическом пути. При этом сеть имеет опрокинутую нумерацию, то есть источник номер n+1, а стоки, которых возможно несколько имеют первые номера.

Решим полученную задачу на примере. Пусть имеется 8 работ, для которых заданы , .

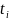i	ti	Ii+
1	5	-
2	2	-
3	3	1
4	7	1, 2
5	4	2, 3
6	6	2, 4
7	5	4, 6
8	2	5, 6

Рис. 3.3

Введем 9 работу, для которой t₉ = 0, а I₉⁺ - все завершающие работы.

Завершающими работами являются те работы, которые не перечислены ни в одном из .

i	ti	Ii+
1	5	-
2	2	-
3	3	1
4	7	1, 2
5	4	2, 3
6	6	2, 4
7	5	4, 6
8	2	5, 6
9	0	7, 8

Рис. 3.4

Решить задачу о критическом пути можно не только с помощью графа или матрицы смежности, но и с помощью заданных I_i⁺ . В самом деле, как следует из модели (3.16) – (3.19)

(3.20)

и

(3.21)

j_i : 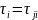+ (3.22)

Для дальнейшего анализа задачи введем граф и I_i^- , где I_i^- - множество работ, непосредственно следующих за i – ой работой.

I_i^- легко определяется, если известно I_i⁺ . Так как j I_i^- , если i I_j⁺ .

Теперь решим задачу о критическом пути:

i	ti	Ii+	τi	ji
1	5	-	0
2	2	-	0		4, 5, 6
3	3	1	5	1	5
4	7	1, 2	5	1
5	4	2, 3	8	3	8
6	6	2, 4	12	4
7	5	4, 6	18	6
8	2	5, 6	18	6	9
9	0	7, 8	23	7

Рис. 3.5

Получим, длина критического пути равна 23.

Критический путь равен - 9-7-6-4-1 или 1-4-6-7-9.

Проанализируем полученные результаты: длина критического пути совпадает с минимальным временем выполнения проекта, таким образом, можем выписать ответ.

Ответ: минимальное время выполнения проекта равно 23.

Как следует из вербальной модели, теперь необходимо разработать календарный план (график) выполнения работ.

Календарный план будем составлять по следующей схеме:

N	Начало раннее (НР)	Начало позднее (НП)	Окончание раннее (ОР)	Окончание позднее (ОП)	Интервал	Резерв (Р)
Критические работы
Некритические работы

Рис. 3.6

Работы, стоящие на критическом пути не имеют резерва. Поэтому для них НР и Р равны и они должны выполняться непосредственно одна за другой, если же работа не стоит на критическом пути, можно сдвигать право, однако при этом надо учитывать, что этот сдвиг не должен удлинять общее время управления проекта.

Выпишем формулы для всех столбцов рис. 3.6 :

НР_i = τ_i, ОР_i = НР_i + t_i , (3.23)

Инт._i = (НР_i, ОП_i) (3.24)

Резерв_i = НП_i – HP_i = ОП_i – OP_i = ОП_i - HP_i – t_i. (3.25)

Для работ стоящих на критическом пути:

НП_i = НР_i, ОП_i = ОР_i, (3.26)

Для работ, нестоящих на критическом пути.

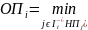(3.27)

НП_i = ОП_i – t_i . (3.28)

Представим календарный план (график) для рассмотренного ранее примера:

№	НР	ОР	НП	ОП	Интервал	Резерв
1	0	5	0	5	(0; 5)	0
4	5	12	5	12	(5; 12)	0
6	12	18	12	18	(12; 18)	0
7	18	23	18	23	(18; 23)	0
9	23	23	23	23	(23; 23)	0
2	0	2	3	5	(0; 5)	3
3	5	8	14	17	(5; 17)	9
5	8	12	17	21	(8; 21)	9
8	18	20	21	23	(18; 23)	3

Рис. 3.7

???Задание для самостоятельной работы:

Решить задачу:

i	1	2	3	4	5	6	7	8	9	10
ti	5	2	3	7	4	6	5	2	5	3
Ii+	-	-	-	1,2	2,3	2,4	4,6	5,6	6,7	5,8

Для каждого варианта определены номера работ, которые исключаются (не учитываются в рамках данной конкретной задачи; если номер исключённой работы встречается в каком-либо множестве предшествующих работ, то его необходимо исключить из этого множества).

Работы, которые исключаются:

Номер варианта	1	2	3	4	5	6	7	8	9	10	11	12
Исключаемые номера работ	1,4	1,6	2,6	2,4	2,7	3,5	3,8	3,9	7,9	9,10	8,10	7,8

13	14	15	16	17	18	19	20	21	22	23	24	25
2,10	1,3	3,10	4,6	4,8	4,10	5,7	5,9	6,7	6,10	3,4	4,9	1,9