Задачи о кратчайшем и критическом пути.

Постановка задачи: дана сеть без контуров с одним источником и одним стоком, c_ij – длины дуг.

1. Требуется найти кратчайший путь от источника к стоку.

2. Требуется найти критический (самый длинный) путь от источника к стоку.

Построим математическую модель, сведя нашу задачу к сетевой транспортной:

Если источнику присвоить значение T₁=1, стоку – T_n=-1, а T_i=0для 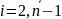, то можем записать соответствующую транспортную задачу:

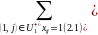
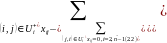
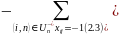
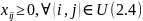
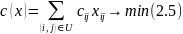
Так как в правой части стоят только целые числа, то все потоки будут равны либо 1, либо 0, значит:

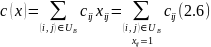
где c_ij–длина дуги.

Таким образом, мы можем свести задачу о кратчайшем пути к сетевой транспортной задаче. В задаче о критическом пути ограничения сохраняются, для целевой функции ищется максимум.

???Задание для самостоятельной работы:

1. Можно ли решить задачу о кратчайшем пути для сети с контуром?

2. Можно ли решить задачу о кратчайшем пути для сети с контурами?

Метод решения задач о кратчайшем и критическом пути.

Вместо полученной сетевой транспортной задачи будем решать двойственную, которая имеет вид:

- для кратчайшего пути - для критического пути

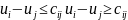
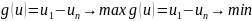
Рассмотрим задачу о кратчайшем пути:

положим u_n= 0, тогда получаем

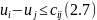
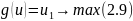
Выпишем ограничения для u₁ в виде:

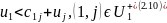
Таким образом, чтобы найти u₁ – максимальное, надо чтобы все u_i были максимальными. Перепишем все ограничения в виде:

Так как , то для 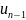имеем одно ограничение:

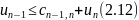
И максимальное значение:

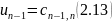
Пусть теперь найдены потенциалы (i-1)вершины из (2.11). Следует, что максимальное значение 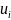будет равно:

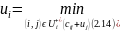
Таким образом, последовательно можно найти потенциалы всех вершин, при этом 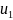будет равно длине кратчайшего пути, что следует из теории двойственности.

Теперь необходимо найти сам путь. Для этого надо вернуться к рассмотрению исходной задачи. В путь войдут те дуги, по которым потоки 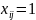, но это базисные дуги, следовательно для них .

Таким образом, для того чтобы определить базисные дуги, надо в формуле (2.14) для каждого iопределить номер j,на котором это равенство достигается.

Поэтому при вычислении u_i введем пометку 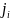для номера вершины, на которой достигается минимум. Тогда путь будет начинаться с вершины с номером 1, и переходить к вершинам, указанным в пометках.

Для задачи о критическом пути производятся те же вычисления, только в формуле (2.14) заменим на .

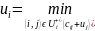Алгоритм:

Шаг 1.Полагаем u_n =0.

Шаг 2.Цикл по i =

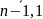
2.1

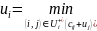
2.2 Определяется

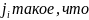
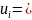
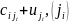
Шаг 3.Выписывается ответ: длина кратчайшего пути L_крат. = u₁.

Шаг 4.Строится кратчайший путь 1 – j₁ – 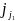– … – n.

Обозначим через U_крат. множество вершин, вошедших в кратчайший путь.

Шаг 5.Вычисление:

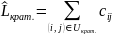
Шаг 6.Проверка равенства:

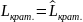
Замечание 2.3. При решении задачи о критическом пути в алгоритме необходимо заменить на втором шаге min на max.

Рассмотрим пример использования приведённого выше алгоритма:

Н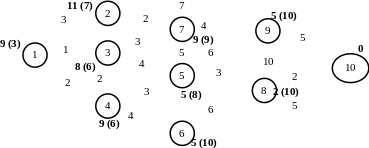 айдём кратчайший путь

Рис. 2.6

L_крат. = 9

Кратчайший путь: 1– 3 – 6 – 10

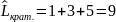
Н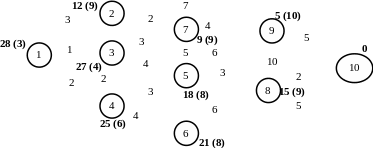 айдём критический путь

Рис. 2.7

L_крит. = 28

Критический путь: 1– 3 – 4 – 6 – 8 – 9 – 10

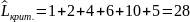
???Задание для самостоятельной работы:

Решить задачу о кратчайшем и критическом пути, используя граф, изображённый на рис. 3.5, заменив веса трёх указанных дуг новыми значениями, приведёнными ниже:

1. c_1,3 = 5, c_3,6 = 11, c_5,6 = 13.

2. c_2,5 = 7, c_6,8 = 14, c_8,10 = 1.

3.c_1,4 = 10, c_3,4 = 2, c_11,14 = 13.

4.c_8,9 = 10, c_9,11 = 4, c_13,14 = 11.

5.c_1,2 = 8, c_6,8 = 1, c_10,11 = 12.

6.c_4,10 = 6, c_8,10 = 17, c_5,6 = 10.

7.c_3,4 = 16, c_7,8 = 3, c_11,12 = 12.

8.c_1,3 = 1, c_2,5 = 14, c_2,9 = 19.

9.c_10,13 = 7, c_11,13 = 15, c_8,10 = 4.

10.c_5,6 = 8, c_7,10 = 8, c_10,13 = 1.

11.c_1,4 = 16, c_4,7 = 5, c_8,9 = 1.

12.c_1,3 = 1, c_3,4 = 16, c_3,5 = 12.

13.c_7,8 = 7, c_7,10 = 5, c_8,10 = 2.

14.c_11,12 = 16, c_12,14 = 1, c_11,13 = 15.

15.c_10,11 = 12, c_9,11 = 4, c_9,12 = 18.

16.c_6,8 = 8, c_7,8 = 2, c_5,9 = 12.

17.c_2,9 = 1, c_3,6 = 10, c_3,7 = 17.

18.c_2,5 = 1, c_5,6 = 6, c_8,10 = 10.

19.c_7,10 = 2, c_8,10 = 9, c_9,11 = 11.

20.c_3,4 = 5, c_4,10 = 13, c_11,14 = 13.

21.c_9,12 = 18, c_12,14 = 3, c_11,12 = 16.

22.c_5,6 = 1, c_2,5 = 9, c_1,2 = 17.

23.c_9,11 = 17, c_10,11 = 6, c_11,13 = 2.

24.c_7,8 = 16, c_1,3 = 17, c_6,8 = 1.

25.c_7,10 = 14, c_9,11 = 2, c_512,14 = 8.