Построение математической модели.

Введем x_ij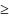 0 – поток по дуге. Разобьём все вершины на три подмножества:

- N₁ - множество источников (T_i> 0);

- N₂ - промежуточные вершины ( );

- N₃ - множество вершин – стоков ( ).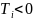

Из каждой вершины N₁ вся продукция должна быть вывезена:

В каждый сток должно быть привезено продукции ровно столько, сколько требуется:

Для промежуточных вершин выполняется:

И функция цели примет вид:

Таким образом, мы получили модель сетевой транспортной задачи.

Выпишем окончательный вид модели:

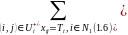
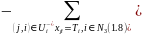
Замечание 1.1 Известно, что для матричной транспортной задачи, условие баланса является необходимым и достаточным условием совместности. Для сетевой транспортной задачи ∑Ti = 0 является только необходимым условием совместности.

???Приведите пример сетевой транспортной задачи, в которой условие баланса выполняется, но она является несовместной.

Замечание 1.2. В модели (1.6) - (1.10) можно исключить ограничения (1.6) и (1.8).

???Почему?

Замечание 1.3. Матрица инциденций — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро (дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность). В случае ориентированного графа каждому ребру (x, y) ставится в соответствие -1 на позиции [x, y] и 1 на позиции [y, x]; если связи между вершинами нет, то ставится в соответствие 0.

Заметим, что матрица ограничений сетевой транспортной задачи и есть матрица инциденций.

Метод потенциалов для сетевой транспортной задачи.

Метод потенциалов включает в себя четыре этапа.

Краткая характеристика этапов и алгоритмы:

Этап 1. Построение начального базисного решения.

Этап 2. Проверка имеющегося решения на оптимальность:

- если решение оптимально, то переход к этапу IV,

- иначе переход к этапу III.

Этап 3. Перестроение базисного решения и переход к этапу II.

Этап 4. Вычисление значения целевой функции.

Этап I. Построение начального базисного решения.

Базисом в сетевой транспортной задаче является дерево. При этом необходимо построить не любое дерево, а такое, по которому можно распределить все потоки. Задача решается с помощью введения новых вершин и дуг.

Алгоритм:

Шаг 1.Вводится вершина с номером i = 0 и интенсивностью T_i = 0.

Шаг 2. Все вершины, имеющие положительные интенсивности T_i 0 связываются с нулевой вершиной входящими дугами с целевым коэффициентом c_i0 = 0 и потоком [x_i0] = Т_i.

Шаг 3. Вводится вершина с номером i = n+1 и интенсивностью T_i=­ 0.

Шаг 4. n + 1 вершина связывается с вершинами, имеющими Т_i< 0, исходящими дугами с c _{(n+1) i} = 0 и с потоком [x_{(n+1) i}] = |T_i|.

Шаг 5. Вводится дуга (0, n+1)cc_{0 (n+1)} = М, М – достаточно большое число, с потоком [x_{0 (n+1)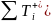}] = (T_i⁺> 0).

Шаг 6. Вершины, имеющие нулевую интенсивность , связываются с вершинами дерева дугами графа (i₀, j) или (j, i₀),

где , и с потоком .

Замечание. Для вершин с Т_i = 0 можно в шаге 2 или шаге 4 поставить нестрогое неравенство, тогда шаг 6 будет отсутствовать.

Этап II. Проверка базисного решения на оптимальность.

Пусть задана задача линейного программирования в канонической форме:

Пусть имеется базисное решение:

где , состоящий из линейно-независимых столбцов матрицы .

Для проверки имеющегося допустимого решения на оптимальность используется следующая идея:

Выписывается двойственная задача:

(A)

Берутся базисные ограничения двойственной задачи и записываются в виде равенств:

(B).

Получаем систему с квадратной невырожденной матрицей, у которой есть единственное решение, пусть 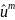– решение системы (B).

Далее вычисляются оценки:

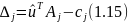
если верно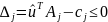 или 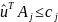, то найдено оптимальное решение задачи.

Если же такое, что 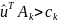, то решение не оптимально и значение должно быть увеличено.

Перейдем к рассмотрению транспортной задачи.

Выпишем задачу двойственную к транспортной. Она будет иметь следующий вид:

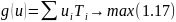
Каждое двойственное ограничение соответствует дуге, а каждое u_i – i-той вершине, u_i называются потенциалами задачи, поэтому метод носит название метод потенциалов.

Обозначим множество дуг дерева через и запишем , . Так как дерево имеет n вершин, и(n-1) дугу, то полученная система уравнений является системой, состоящей из(n-1) уравнения с n неизвестными, следовательно, имеет бесчисленное множество решений.

Поэтому один из потенциалов можно положить, равным нулю и затем найти значения всех остальных потенциалов.

Замечание1. 4. Удобнее полагать равным нулю потенциал вершины, которая является стоком.

Алгоритм:

Шаг 1. Выписывается система уравнений, соответствующих дугам дерева .(B)

Шаг 2. Потенциал одного из стоков полагаем равным нулю: .

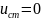Шаг 3. Остальные потенциалы вычисляем из системы уравнений (B).

Шаг 4. Для всех дуг графа вычисляется разность потенциалов и сравнивается с собственным .

Шаг 5. Если , то переходим к этапу IV, иначе – к этапу III.

Замечание 1.5. Так как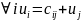 , то пока дереву принадлежит дуга с целевым коэффициентом 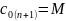, остальные можно положить равными нулю .

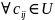Этап III. Перестроение базисного решения.

Пусть .

Алгоритм:

Шаг 1. Дуга присоединяется к дереву.

Шаг 2.Отыскивается цикл, связывающий с дугами дерева (такой цикл существует, и он единственный, что следует из свойств дерева).

Шаг 3.При движении по циклу в направлении дуги на дугах цикла расставляются знаки:

“+” – по сонаправленной дуге,

“–“ – по противоположно направленной.

Шаг 4. Определяется 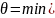(минимум из дуг со знаком “ – “).

Шаг 5. Потоки по дугам, входящим в цикл, пересчитываются по формулам: Потоки по непомеченным дугам не пересчитываются.

Шаг 6. Одна из дуг цикла, помеченная знаком “–“, поток по которой стал (или был) равным нулю, исключается из дерева (удобнее исключать дуги с большими значениями c_ij).

Шаг 7. Переход к этапу II.

Замечание 1.6. Полезно проверять условия баланса по вершинам для контроля арифметических ошибок, то есть

Для каждой вершины сумма входящих потоков плюс интенсивность должны равняться сумме исходящих потоков.

Замечание 1.7. Фиктивные вершины исключаются, тогдаx_0n+1=0, при этом исключаются три дуги, то есть дуги (0, n+1); (i, 0); (n+1,i).

Замечание 1.8. Стоимости c_ij возвращаются в алгоритм тогда, когда фиктивные вершины исключаются из дерева.

Замечание 1.9. Сетевая транспортная задача несовместна, если , но при этом остается х_0n+1 >0.

Замечание 1.10.Из теории двойственности следует, что на оптимальных решениях исходной и двойственной задач значения целевых функций этих задач совпадают.

Этап IV. Вычисление значения целевой функции

Шаг 1. Если х_0n+1 >0, то вписывается ответ: задача несовместна. Иначе шаг 2.

Шаг 2. Вычисление значения целевой функции по формуле

Шаг 3. Вычисление значения целевой функции двойственной задачи

Шаг 4. Проверка равенства c(x) = g(u)(на оптимальном решении значение целевой функции исходной и двойственной задач совпадает).

Рассмотрим метод потенциалов на примере.

Пусть задан ориентированный граф.

Рис. 1.3

Построим начальное базисное дерево:

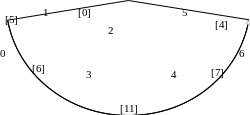
Рис 1.4

В рассматриваемом примере:

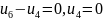
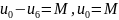
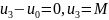
П роверка на оптимальность:

Рис 1.5

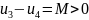
То есть решение не оптимально и дугу (3,4) можно присоединить к дереву. Теперь найдем цикл, связывающий дугу (3,4) с дугами дерева. Это будет цикл: (3,4), (4,6), (6,0), (0,3). Заметим, что все дуги противоположно ориентированы и на них следует поставить знак минус (см. рис. 1.5). В соответствие с алгоритмом этапа II будем иметь , то есть дуга (3,0) будет исключена из базиса.

Н а рис 1.6. представлено новое базисное решение:

рис. 1.6

После нескольких итераций получится следующее базисное решение:

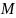
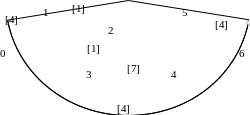
Рис 1.7

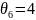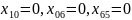Т о есть дугу (4,5) можно присоединить к дереву. Видим, что цикл связывает все вершины дерева и . После пересчета величин потоков получим: , то есть вершины нулевая и шестая вместе с соответствующими дугами можно отбросить, и получится распределение потоков по соответствующим дугам графа.

Рис 1.8

Теперь при вычислении потенциалов необходимо задействовать настоящие значения .

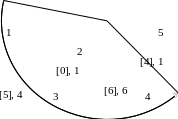
Рис. 1.9

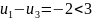
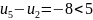
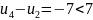
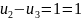
• Решение найдено.

Вычислим теперь:

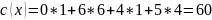
Решение найдено верно.

???Задание для самостоятельной работы:

Методом потенциалов решить сетевую транспортную задачу для графа, заданного на рис. 1.3, если даны интенсивности двух вершин, для остальных вершин интенсивности задаются самостоятельно, учитывая условие баланса.

1. T₂ = 6, T₅ = 7. 13. T₁ = - 10, T₅ = 1.

2. T₁ = - 9, T₄ = - 4. 14. T₄ = - 4, T₅ = 2.

3. T₃ = - 2, T₅ = 6. 15. T₂ = 1, T₃ = - 6.

4. T₂ = 2, T₄ = - 5. 16. T₁ = - 2, T₃ = - 6.

5. T₂ = 1, T₃ = - 4. 17. T₃ = - 7, T₅ = 10.

6. T₁ = - 9, T₅ = 4. 18. T₂ = 6, T₃ = - 1.

7. T₄ = - 2, T₅ = 8. 19. T₁ = - 2, T₅ = 7.

8. T₂ = 1, T₅ = 9. 20. T₁ = - 7, T₃ = - 9.

9. T₁ = - 5, T₂ = 9. 21. T₁ = - 9, T₂ = 1.

10. T₃ = - 3, T₄ = 7. 22. T₂ = 3, T₄ = - 9.

11. T₃ = - 8, T₅ = 10. 23. T₂ = 10, T₃ = - 5.

12. T₂ = 8, T₅ = 1. 24. T₄ = - 6, T₅ = 1.

25. T₃ = - 8, T₄ = - 4.