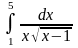2.7.2. Вычисление длин дуг плоских кривых.

В элементарной геометрии измерялись длины прямолинейных отрезков, а также длина окружности и ее частей. За длину окружности принимается предел периметров правильных вписанных в окружность многоугольников при неограниченном увеличении числа их сторон. Обобщим это понятие для любой кривой.

Определение. Длиной L дуги АВ называется предел, к которому стремится периметр вписанной в эту дугу ломанной, когда число ее звеньев неограниченно растет, а наибольшая из длин звеньев стремится к нулю:

Кривые, для которых этот предел существует, называются спрямляемыми.

Теорема. Пусть кривая АВ задана уравнением y=f(x), где f(x) – непрерывная функция, имеющая непрерывную производную во всех точках сегмента [a;b]. Тогда дуга АВ имеет длину:

,

Пример 1. Найти длину дуги полукубической параболы от х=0 до х=5. Решение: Кривая симметрична относительно оси Ох. Найдем длину верхней ветви кривой. Из уравнения находим . Далее, применяя формулу, получим = (ед.)

Пример 2. Вычислить длину дуги параболы у²=4х от х=0 до х=1.

Решение.

Д ля наглядности выполним чертеж.

Для нахождения длины дуги параболы можно воспользоваться формулами:

Так как Тогда по формуле (1) получим:

Этот интеграл довольно сложный. Поэтому воспользуемся формулой (2)

Для этого выразим из уравнения параболы х и найдем производную по «игреку»:

Тогда длина дуги будет равна:

Замечание.

2.7.3. Вычисление объемов тел вращения.

2.7.3.1. Вычисление объема тела по известным площадям параллельных сечений. Если известны площади сечений тела плоскостями, перпендикулярными оси OX, т. е., зная х, мы можем вычислить площадь сечения S = S (x). Тогда объем тела в предположении, что S(x) - интегрируемая функция.

2.7.3.2. Вычисление объема тела вращения:

а) если тело образовано вращением криволинейной трапеции, ограниченной кривой y = f (x), осью OX и двумя прямыми x = a и x = b (a < b) вокруг оси OX, то объем тела ;

б) если тело образовано вращением фигуры, ограниченной кривой , прямыми y=c, y=d (c<d) и осью OY, вокруг оси OY, то его объем ;

в) если тело образовано вращением вокруг оси OY фигуры, ограниченной линией y = f (x), прямыми x = a, x = b и осью OX, то его объем можно вычислить по формуле

Примеры.

а) Вычислить объем тела, полученного вращением фигуры, ограниченной линиями вокруг оси Ох.

Решение.

Р

Искомая плоская фигура заштрихована, именно она и вращается вокруг оси Ох. Поэтому воспользуемся формулой

Пределы интегрирования легко определяются по чертежу: а=0, b=2. Плоская фигура ограничена графиком параболы сверху. Это и есть та функция, которая подразумевается в формуле.

В практических заданиях плоская фигура иногда может располагаться и ниже оси Ох. Это ничего не меняет – функция в формуле возводится в квадрат, таким образом, объем тела вращения всегда неотрицателен

ешение начинается с чертежа плоской фигуры. То есть, на координатной плоскости необходимо построить фигуру, ограниченную линиями , при этом уравнение задаёт ось Ох.

Вычислим объем тела вращения, используя данную формулу:

Ответ:

b) Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями .

Решение.

Изобразим на чертеже плоскую фигуру, ограниченную заданными линиями, не забывая при этом, что уравнение х=0 задает ось Oy.

Искомая фигура заштрихована. При её вращении вокруг оси Oх  получается такой сюрреалистический бублик с четырьмя углами.

Объем тела вращения вычислим как разность объемов тел.

Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси Ох  получается усеченный конус. Обозначим объем этого усеченного конуса через V₁.

Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси Ox, то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через V_2.

И, очевидно, разность объемов V=V₁-V₂ – в точности объем нашего «бублика».

Используем стандартную формулу для нахождения объема тела вращения:

1. Фигура, обведенная красным цветом ограничена сверху прямой y=x+4, поэтому:

2. Фигура, обведенная зеленым цветом ограничена сверху прямой y=2x+1, поэтому:

3) Объем искомого тела вращения:

Ответ:

В данном случае решение можно проверить, используя школьную формулу для вычисления объема усеченного конуса:

с) Вычислить объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривыми

Решение.

Выполним чертеж:

Для цели нахождения объема тела вращения достаточно использовать правую половину фигуры, которая заштрихована. Обе функции являются четными, их графики симметричны относительно оси Oy, симметрична и фигура. Таким образом, заштрихованная правая часть, вращаясь вокруг оси Oy, непременно совпадёт с левой не штрихованной частью.

Поскольку фигура получена вращением вокруг оси Oy, воспользуемся формулой:

Для этого необходимо перейти к обратным функциям, то есть, выразить «иксы» через «игреки»:

Обратите внимание, что правой ветви параболы соответствует обратная функция . Левой неиспользуемой ветви параболы соответствует обратная функция . В таких случаях возникает вопрос, какую же функцию выбрать? Для выбора обратной функции необходимо взять любую точку правой ветви (например, (1;1)) и подставить ее координаты в функцию . Координаты подошли, значит, функция задает именно правую ветвь, а не левую.

Тоже самое и с функций Не всегда бывает сразу понятно, какую обратную функцию выбрать: . Выбрать функцию поможет подстановка в найденную обратную функцию точек графика.

Если повернуть систему координат на 90, то:

– на отрезке [0;1] над осью Oy расположен график функции

– на отрезке [1;2] над осью Oy расположен график функции .

Следовательно, объем тела вращения нужно искать как сумму объемов тел вращений.

В данном случае:

Ответ:

Задания для практической работы №4.

1.Вычислить неопределенные интегралы.

Вариант	а ) Вычислить интегралы методом непосредственного интегрирования:	б) Вычислите интегралы методом замены переменной или подведением под знак дифференциала.	в) Вычислите интеграл методом интегрирования по частям.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2. Предварительно выполнив чертеж, найти площадь фигур, ограниченных линиями.

Вариант	Уравнения линий
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

3. Определить объем тела, образованного вращением вокруг координатной оси (для четных вариантов – вокруг оси Ох, для нечетных вариантов – вокруг оси Oy) , ограниченного линиями:

Вариант	Уравнения линий
1
2
3
4
5
6
7
8	,
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Срок сдачи практической работы

ОП-253	28.03.2014
ОП-254	21.03.2014

Полякова И.А. Лекции по математике. Технический профиль. 2 курс.