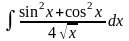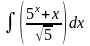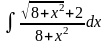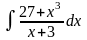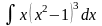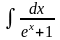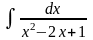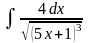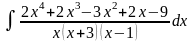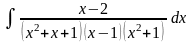2.5.5. Интегрирование рациональных дробей.

Определение. Рациональной дробью называется выражение, заданное в виде отношения двух многочленов: -многочлены, n и m – их степени.

Дробь называется правильной, если .

Дробь называется неправильной, если .

Если дробь неправильная (т.е. ), то всегда с помощью деления на 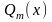рациональную дробь можно представить в виде суммы некоторого многочлена и правильной рациональной дроби , ( ):

.

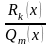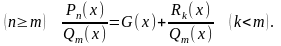Пример 1. Представим дробь в виде суммы многочлена и правильной рациональной дроби:

Таким образом, .

Типы правильных рациональных дробей:

1. ,

2. ,

3. ,

4.

I. Интегрирование рациональных дробей I типа.

.

Пример 1.

.

Пример 2.

II. Интегрирование рациональных дробей II типа.

Пример 1.

Пример 2.

III. Интегрирование рациональных дробей III типа.

, где 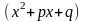- не имеет действительных корней.

Способ интегрирования – замена , тогда

.

Положим ;

Имеем

Пример 1.

.

Таким образом, имеем:

.

Пример 2.

.

Таким образом, имеем:

2.5.6. Представление правильной рациональной дроби в виде суммы простейших

Для представления рациональной дроби в виде суммы простейших дробей используется метод неопределенных коэффициентов. Любую правильную дробь можно представить в виде суммы простейших рациональных дробей четырёх типов по следующему алгоритму:

1. Разлагаем знаменатель правильной рациональной дроби на множители степени не выше второй (Причём вторую степень можно оставлять лишь в том случае, когда нет действительных корней в множителе знаменателя, то есть D<0).

2. В числителе ставим просто буквы А, В, С, … - если корни действительные и выражения вида Мх+N, Сх+D, … - если корни мнимые.

3. Если корни кратные, то слагаемых будет столько, какова кратность корня, причем степени знаменателя понижаются на единицу, начиная с высшего показателя до первого.

4. Неизвестные коэффициенты А, В, С, М, ... находят методом неопределённых коэффициентов.

Например, представим дроби в виде суммы простейших, не находя коэффициентов.

а)

;

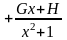б)

.

Рассмотрим пример представления правильной рациональной дроби в виде суммы простейших.

Найдём A, M, N, P, Q методом неопределённых коэффициентов.

Дроби равны и знаменатели равны, следовательно, числители дробей тоже равны. Приравняем коэффициенты при одинаковых степенях переменного.

Если знаменатель имеет только действительные корни, то можно пользоваться другим приёмом: в полученном тождестве придавать переменному значения равные корням знаменателя.

Например:

;

;

При имеем ;

Следовательно, .

Иногда пользуются обеими методами сразу.

Рассмотрим интегралы, которые сводятся с помощью разложения методом неопределённых коэффициентов к интегралам от простейших рациональных дробей I, II и III типов

Пример 1. Найти .

Решение.

Две дроби с одинаковыми знаменателями равны, если равны их числители:

раскроем скобки, и приведём подобные члены:

два многочлена равны между собой, если равны коэффициенты при одинаковых степенях х. Приравниваем коэффициенты при одинаковых степенях х:

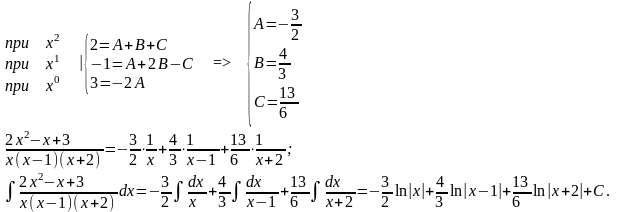
Пример 2. Найти

Решение.

Рациональнее здесь будет воспользоваться комбинированным методом. Сначала подставим, корни знаменателя х = 0 и х = -1 в обе части равенства, получим

если х = 0, то А=2,

если х = -1, то В=1.

А затем, приравняем коэффициенты при и в левой и правой части равенства:

Итак, А=2, В=1, D= -2, С= -2.

Поэтому

Пример 3. Найти .

Решение.

Задания для практической работы №3.

1.Вычислить интегралы методом непосредственного интегрирования:

Вариант	а	б	в
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2.Вычислите интегралы методом замены переменной или подведением под знак дифференциала.

Вариант	а	б
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

3. Вычислите интеграл методом интегрирования по частям.

Вариант		Вариант
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

4. Вычислить интеграл, разложив подынтегральную функцию на сумму простейших рациональных дробей.

Вариант		Вариант
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Срок сдачи практической работы

ОП-253	26.02.2014
ОП-254	26.02.2014

Полякова И.А. Лекции по математике. Технический профиль. 2 курс.