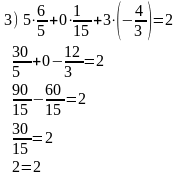3.Метод обратной матрицы.

Пусть дана система линейных алгебраических уравнений, содержащая n уравнений и n неизвестных

,

Такую систему удобно записывать в компактной матричной форме

AX=B

Здесь А — матрица коэффициентов системы, называемая основной матрицей;

Х— вектор-столбец из неизвестных x_j.

В— вектор-столбец из свободных членов b_i.

Произведение матриц А*Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).

Преобразуем матричное уравнение, умножив слева обе его части на матрицу, обратную основной матрице системы:

А^-1(AX)=А^-1B

Умножение матриц ассоциативно, следовательно

(А^-1A)X=А^-1B

По определению обратной матрицы А^-1A=Е – единичная матрица, играющая роль единицы в матричном счислении, т.е. являющаяся нейтральной по отношению к умножению. Получаем:

ЕX=А^-1B  Х= А^-1B

Полученное равенство позволяет отыскать решение системы в виде матрицы – столбца, которая является результатом умножения матрицы, обратной к основной матрице системы, на столбец свободных членов.

Примеры.

а) Решить систему линейных уравнений методом Крамера.

Решение

1. Выписываем матрицу системы и столбец свободных членов:

2. Находим определитель системы:

Определитель отличен от нуля, следовательно, система имеет единственное решение.

3. Находим вспомогательные определители, которые получаются из определителя системы последовательной заменой столбцов коэффициентов при неизвестных на столбец свободных членов:

4. На основании теоремы Крамера:

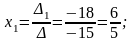
Замечание 1. При кажущейся простоте правила Крамера применяется оно для систем более чем из трех уравнений, только в каких-то исключительных случаях. Дело в том, что вычисление определителей требует выполнения большого числа арифметических операций.

Замечание 2. При решении системы уравнений приходится выполнять довольно большой объем вычислений. Поэтому велика вероятность ошибки. Чтобы обнаружить эту ошибку, рекомендуется выполнить проверку ответа, то есть подставить полученные значения неизвестных в уравнения системы. Если все уравнения превратятся в верные равенства, то решение найдено верно. В противном случае при вычислениях где-то допущена ошибка.

5. Выполним проверку, подставив найденные значения переменных в уравнения системы

в) Решить систему методом Гаусса

Решение.

1

2

3

4

5

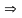
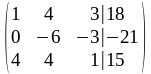
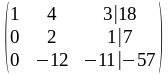
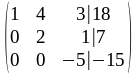
1 шаг. Вторая строка получена как результат сложения первой строки расширенной матрицы, умноженной на (–2), со второй строкой (при этом исключается первая неизвестная во втором уравнении);

2 шаг. Третья строка получена как результат сложения первой строки, умноженной на

(–4), с третьей строкой (исключается первая неизвестная в третьем уравнении);

3 шаг. Вторая строка получена путем умножения ее на ;

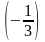4 шаг. Третья строка получена как результат сложения второй строки, умноженной на 6, с третьей строкой (исключается вторая неизвестная в третьем уравнении);

5 шаг. Третья строка получена умножением ее на .

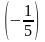Расширенная матрица приведена к ступенчатому виду (под главной диагональю - нули). На этом процесс элементарных преобразований над строками расширенной матрицы заканчивается.

Далее записываем СЛАУ, соответствующую полученной ступенчатой матрице, и являющуюся эквивалентной исходной системе.

Ответ: (1,2,3) – решение единственное.

Так как расширенная матрица приведена к треугольному ступенчатому виду, все переменные определяются однозначно, поэтому система имеет единственное решение.

с) Решить систему методом Гаусса

Решение

1

2

3

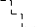
1 шаг. Вторая строка получена как результат сложения первой строки, умноженной на

(–2), со второй строкой (исключаются первая и вторая неизвестные во втором уравнении);

2 шаг. Третья строка получена как результат сложения первой строки, умноженной на

(–1), с третьей строкой (исключаются первая и вторая неизвестная в третьем уравнении);

3 шаг. Третья строка получена как результат сложения второй строки, умноженной на

(-1), с третьей строкой (исключается третья строка);

Расширенная матрица приведена к ступенчатому виду (под главной диагональю - нули). На этом процесс элементарных преобразований над строками расширенной матрицы заканчивается.

Далее записываем СЛАУ, соответствующую полученной ступенчатой матрице, и являющуюся эквивалентной исходной системе.

Расширенная матрица приведена к трапециевидному ступенчатому виду, поэтому система имеет бесконечно много решений. Каждому значению параметра 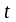соответствует некоторое частное решение.

Например, значению параметра =0 соответствует решение (0,3,3).

d) Решить систему методом Гаусса

Р

1

ешение

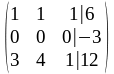
1 шаг. Вторая строка получена как результат сложения первой строки, умноженной на

(–2), со второй строкой.

Полученной второй строке расширенной матрицы соответствует противоречивое выражение:

, которое не выполняется ни при каких значениях неизвестных переменных, поэтому система не совместна (решений нет).

Исследование решений СЛАУ с помощью метода Гаусса

1. Если расширенная матрица системы с помощью элементарных преобразований над строками приводится к треугольному виду, тогда – система имеет единственное решение.

2. Если расширенная матрица системы с помощью элементарных преобразований над строками приводится к трапециевидному виду, тогда – система имеет бесконечное множество решение.

3. Если, в ходе элементарных преобразований над строками расширенной матрицы, образуется строка вида: ( 0 0 0 | b ), b 0, тогда – система решений не имеет.

        Замечание. Так же, как и при решении системы уравнений по правилу Крамера, при использовании метода Гаусса приходится выполнять большой объем вычислительной работы. Из-за этого вполне возможно, что будет допущена какая-либо ошибка в вычислениях. Поэтому желательно после решения системы выполнить проверку, то есть подставить полученные значения неизвестных в уравнения системы. Для выполнения полной проверки подстановку нужно произвести во все уравнения системы. Если же по каким-то причинам это не выполнимо, то можно подставить найденные значения в одно уравнение. В отличие от правила Крамера в методе Гаусса эту подстановку нужно производить в ПОСЛЕДНЕЕ уравнение исходной системы. При наличии в этом уравнении всех неизвестных эта подстановка почти всегда покажет наличие ошибки, если таковая была допущена.

е) Решить систему линейных уравнений методом обратной матрицы.

Решение

1. Составим матричное уравнение АХ=В, где

,

Решение матричного уравнения имеет вид: Х=А^-1В

2. Для нахождения обратной матрицы найдем определитель матрицы А:

,

3. Найдем алгебраические дополнения элементов матрицы :

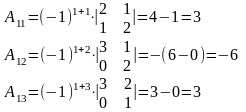
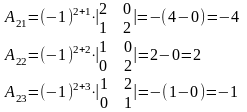
Составим матрицу алгебраических дополнений и транспонируем ее

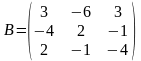
4. Запишем обратную матрицу:

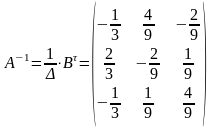
5. Найдем матрицу неизвестных

Итак, решение системы уравнений есть х₁= 4, х₂= 3, х₃= 5.

З

адание для практической работы №1(часть 1)

Дана система линейных уравнений:

Решить данную систему линейных уравнений различными методами (Крамера, Гаусса, методом обратной матрицы).

Значения коэффициентов при неизвестных и свободных членов разных вариантов находятся по таблице Приложение.

Таблица. Приложение

Вариант	а11	а12	а13	а21	a22	a23	a31	a32	a33	b1	b2	b3
1	3	-2	-5	5	-2	-3	1	1	1	0	0	1
2	2	-4	9	7	3	-6	7	9	-9	28	-1	5
3	2	1	-1	3	2	-2	1	-1	2	1	1	5
4	2	3	5	3	5	2	5	2	3	-8	-1	1
5	5	8	1	3	-2	6	2	1	-1	2	-7	-5
6	2	-7	1	3	1	-1	1	-1	3	-4	17	3
7	2	-3	1	1	4	2	1	-4	0	-7	-1	-5
8	3	2	1	5	-2	-2	1	1	-1	3	3	-2
9	3	2	-1	2	-1	3	1	-2	2	4	9	3
10	2	3	5	3	5	2	5	2	3	-6	-3	11
11	5	-5	-4	1	-1	-5	4	-3	-6	-3	11	-9
12	3	-1	0	-2	1	1	2	-1	4	5	0	15
13	1	-2	3	2	3	-4	3	-2	-5	6	20	6
14	5	1	-3	4	3	2	2	-3	1	-2	16	17
15	5	-3	4	2	-1	-2	3	-2	1	11	-6	2
16	1	-2	-1	3	-6	-3	5	-10	-5	2	6	10
17	2	-1	-3	1	3	-4	3	2	-1	0	-11	7
18	-1	2	1	3	-1	6	-4	3	-1	7	19	8
19	2	1	2	3	-1	2	4	-1	5	1	1	-3
20	4	3	2	2	-5	-3	3	2	4	1	16	4
21	3	-2	1	1	5	-2	2	-2	-1	10	-15	3
22	5	-3	4	2	-1	-1	1	-2	1	6	0	0
23	7	-3	5	5	2	1	2	-1	3	32	11	14
24	5	3	3	2	6	-3	8	-3	2	48	18	21
25	2	1	1	-1	-2	2	4	2	1	-4	14	7
26	1	2	1	3	-2	-3	3	-4	5	8	-5	10
27	5	0	4	1	-1	2	4	1	2	1	0	1
28	1	-1	1	2	1	1	1	1	1	6	3	5
29	2	0	-1	1	-1	2	4	1	2	1	0	1
30	1	1	-1	-2	1	1	1	1	1	2	3	6

Полякова И.А. Лекции по математике. Технический профиль. 2 курс.