Квадратичные формы

Цель: научиться приводить квадратичные формы к каноническому виду методом Лагранжа и ортогональным преобразованием, а также изучить различные типы квадратичных форм и критерии их определения.

Литература

[1] / глава 3, § 3.8. [15] / раздел II, § 2.32.

[4] / раздел А, §§ 8.1 – 8.4. [16] / глава 7, § 7.1.

[7] / раздел III, глава 3, §4. [17] / глава VI, §§ 1 – 2.

[8] / глава 8. [18] / глава V, § 7.

[9] / глава VIII. [19] / глава 3, § 3.5.

[12] / тема 3. [20] / глава 9, § 9.4.

Справочный материал

Определение квадратичной формы

Определение1.Квадратичной формой от n переменных называется многочлен с действительными коэффициентами , каждый член которого имеет вторую степень, т.е. многочлен вида

(1)

где числа (коэффициенты квадратичной формы) удовлетворяют условию

Определение2.Матрица ,составленная из коэффициентов квадратичной формы, называется матрицей квадратичной формы, а ее ранг – рангом квадратичной формы.

Из определения квадратичной формы следует, что ее матрица является симметрической, т.е. .

Если , то квадратичную форму (1) можно записать в матричном виде

Линейное преобразование переменных

Определение3.Переход от системы n переменных , , …, к системе n переменных по формулам

(2)

где , называется линейным преобразованием переменных , , …, в переменные

Если , , то линейное преобразование переменных (2) можно записать в матричном виде

, (3)

где матрица называется матрицей линейного преобразования.

Определение4.Если Р – невырожденная матрица, т.е. , то преобразование (3) называется невырожденным.

В этом случае существует обратное преобразование переменных в переменные , , …, :

Если , то преобразование (3) называется вырожденным.

Определение5.Две квадратичные формы f и g называются эквивалентными, если одна из них переводится в другую посредством невырожденного линейного преобразования. Обозначение:

f ~ g.

При невырожденном линейном преобразовании (3) квадратичная форма переходит в эквивалентную квадратичную форму с матрицей .

Канонический вид квадратичной формы

Теорема 1.

Любую квадратичную форму невырожденным преобразованием можно привести к эквивалентной ей форме вида

. (4)

Выражение (4) называется каноническим видом квадратичной формы (оно не содержит попарных произведений переменных), а числа 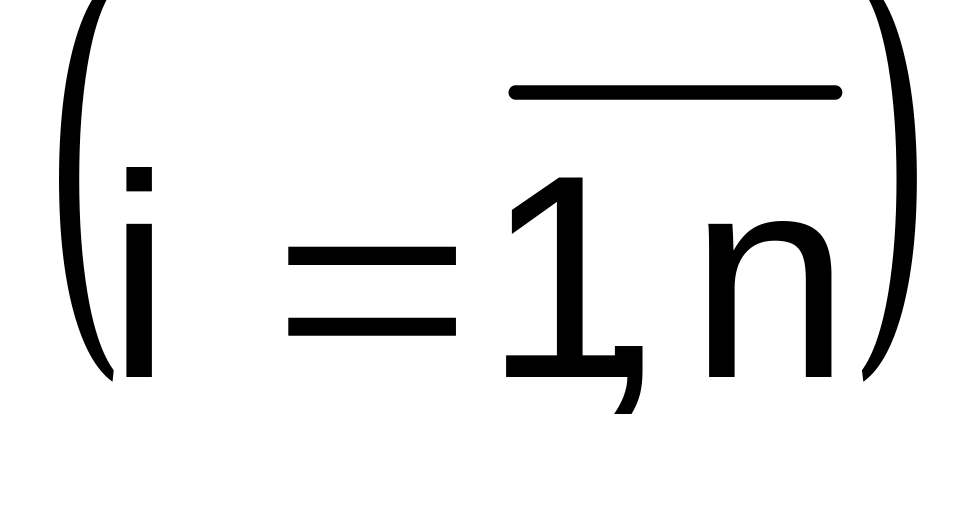- ее каноническими коэффициентами.

Матрица квадратичной формы , имеющей канонический вид (4), является диагональной матрицей с элементами на главной диагонали.

Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду различными методами.