Линейный оператор с простым спектром (простой структуры)

Определение3.Множество всех собственных значений линейного оператора называется спектром линейного оператора.

В спектр линейного оператора каждое собственное значение входит столько раз, какова его кратность в характеристическом многочлене .

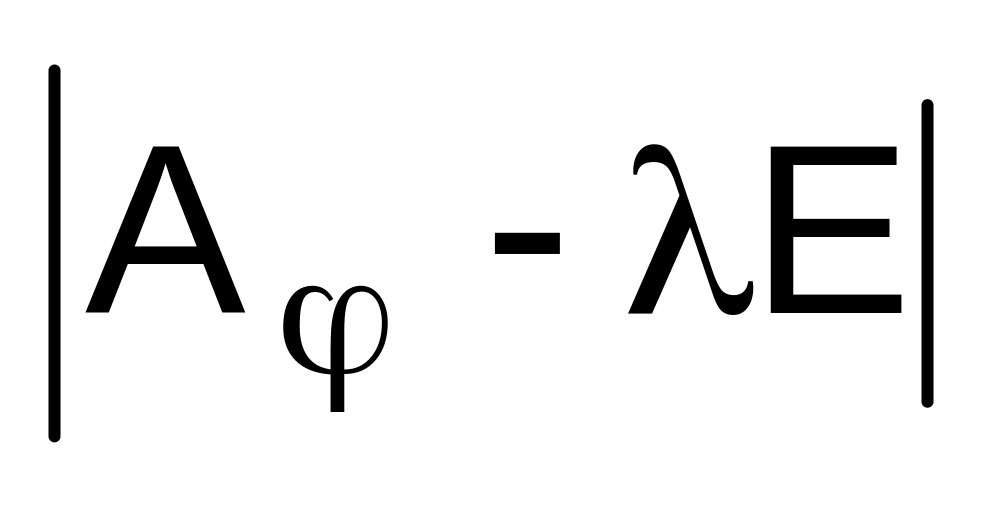Определение4.Линейный оператор , действующий в линейном пространстве , называется оператором с простым спектром или оператором простой структуры, если в пространстве существует базис, состоящий из собственных векторов этого оператора.

Теорема 2 (достаточный признак оператора простой структуры).

Если линейный оператор , действующий в линейном пространстве размерности , имеет попарно различных собственных значений, то отвечающие им собственные векторы образуют базис пространства , и оператор является оператором с простым спектром.

Решение типовых примеров и задач

1. Найти собственные значения и собственные векторы оператора , заданного матрицей

.

Решение.

1.Составим характеристическое уравнение:

или , откуда . Корни этого уравнения и - собственные значения линейного оператора .

2.Найдем собственный вектор , соответствующий собственному значению = . Пусть . Тогда получим:

или = .

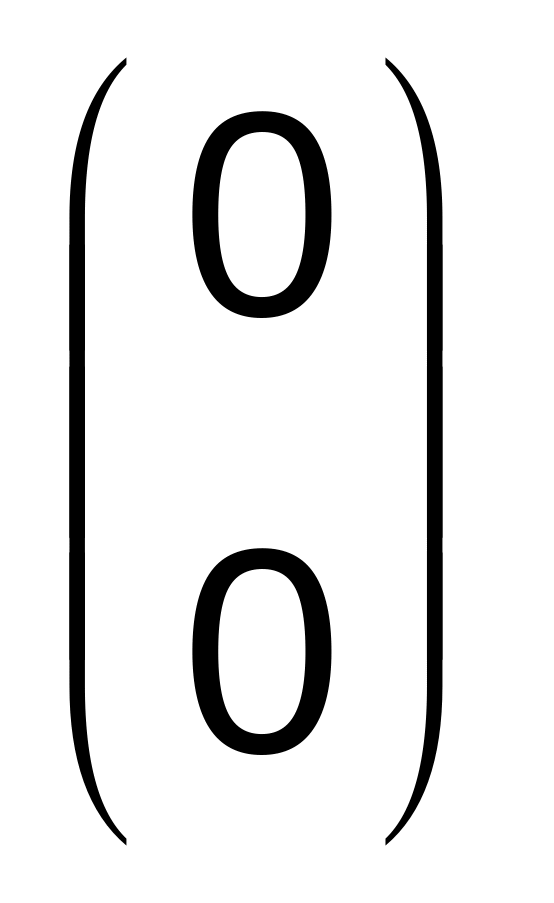Отсюда

= .

Пусть - свободное неизвестное, тогда . Найдем фундаментальную систему решений данной однородной системы (см. пр. зан. №8):

	1	1

.

Следовательно, = = (1, 1), где .

3.Найдем собственный вектор , соответствующий собственному значению Пусть . Тогда получим:

или .

Отсюда

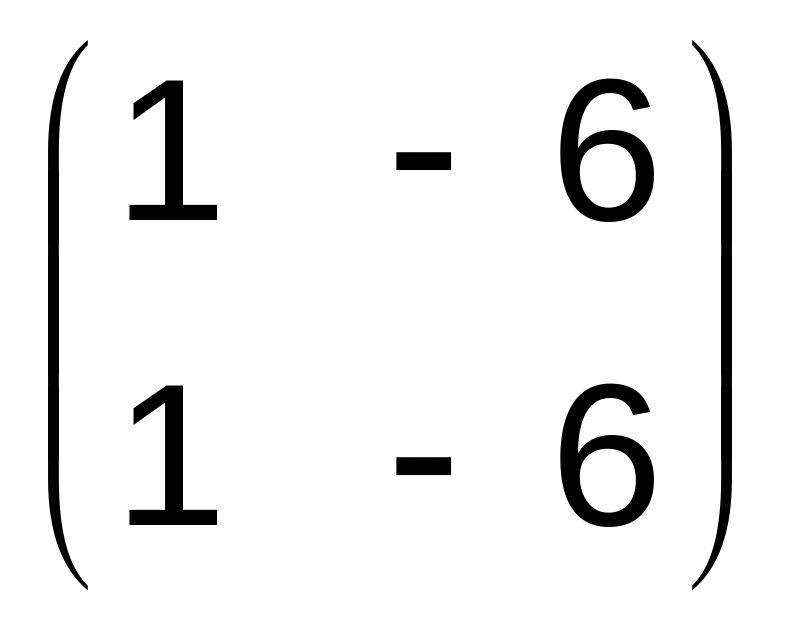
Пусть - свободное неизвестное, тогда х₁=6х₂. Найдем фундаментальную систему решений:

	6	1

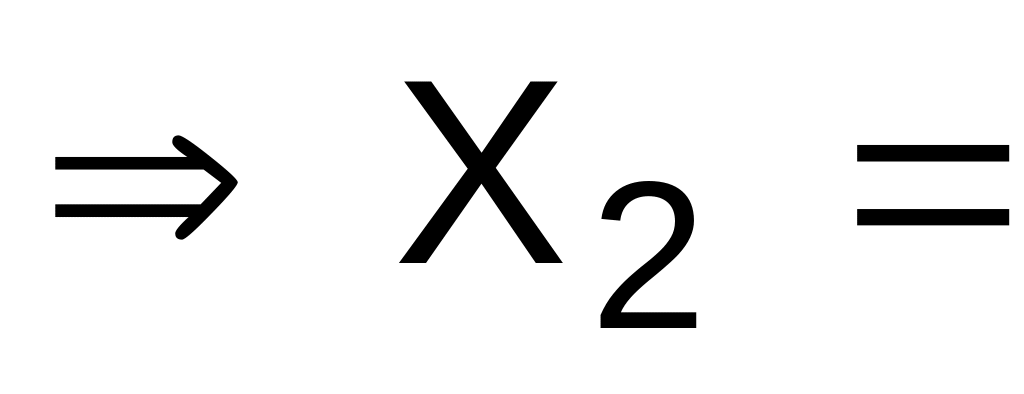
Следовательно, ( 6,1), где

2. Найти собственные значения и собственные векторы матрицы .

Решение.

1.Составим характеристическое уравнение:

После преобразований уравнение примет вид

Решая это уравнение, получим

Корни этого уравнения ₁=₂=9, ₃=-9 - собственные значения матрицы

2.Найдем собственный вектор , соответствующий собственному значению Пусть

Тогда получим

или

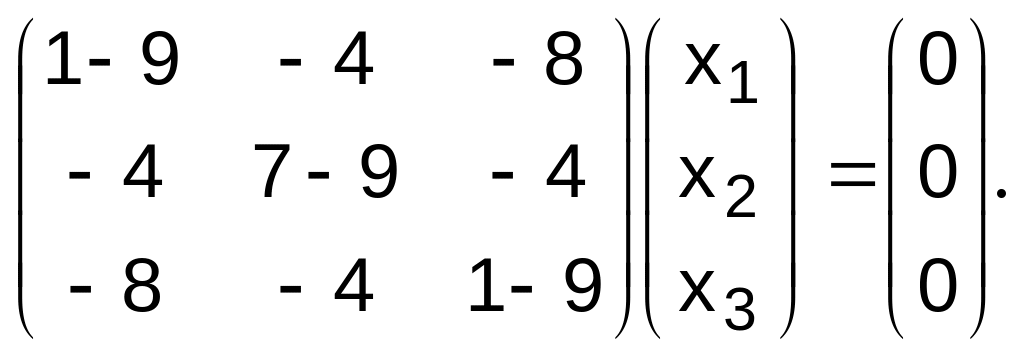
Отсюда

Пусть и - свободные неизвестные, тогда Найдем фундаментальную систему решений данной однородной системы линейных уравнений:

	1	-2	0
	0	-2	1

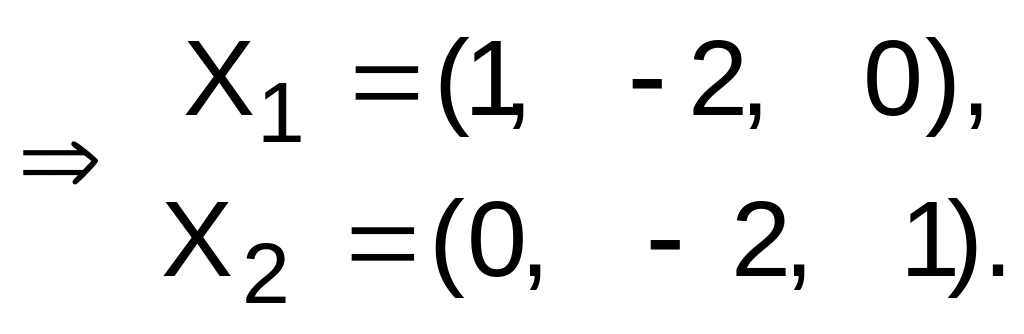
Следовательно, , где числа и не равны нулю одновременно.

3.Найдем собственный вектор , соответствующий собственному значению . Пусть . Тогда получим

или .

Отсюда

Решая последнюю систему методом Гаусса, получим:

.

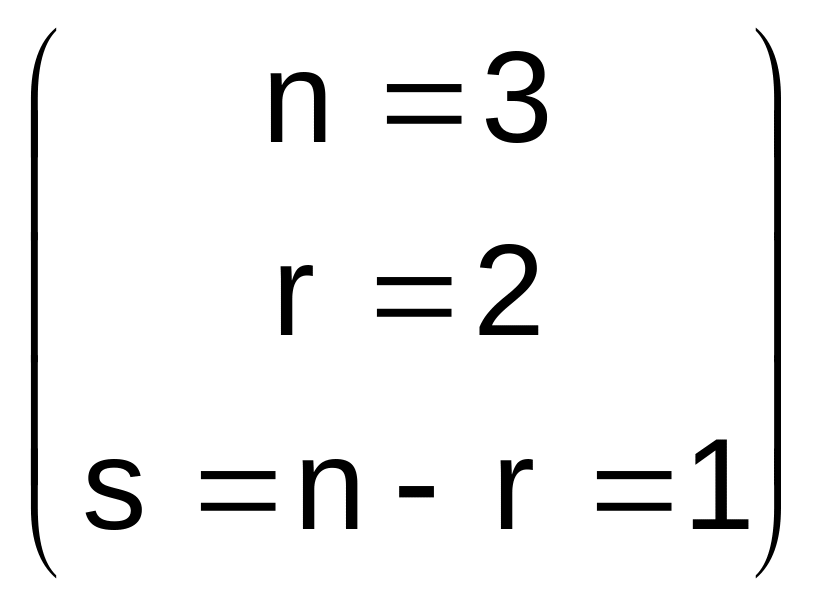Пусть - свободное неизвестное, тогда . Найдем фундаментальную систему решений:

	1	1/2	1

Следовательно, , где .

3. Привести к диагональному виду матрицу линейного оператора .

а) ; б) .

Решение. а) В примере 1 найдены собственные значения оператора и его собственные векторы , где и Так как оператор действует в линейном пространстве размерности 2 и имеет два различных собственных значения, то, отвечающие им собственные векторы и образуют базис данного пространства, в котором матрица оператора принимает диагональный вид

.

б) В примере 2 найдены собственные значения оператора и его собственные векторы и где и не равны нулю одновременно, . Линейный оператор действует в линейном пространстве размерности 3, но имеет два различных собственных значения. Несмотря на то, что , среди собственных векторов, отвечающих данному значению, можно выделить пары линейно независимых векторов (в силу того, что соответствующая фундаментальная система решений содержит два вектора). Следовательно, существует базис из трех собственных векторов, в котором матрица оператора имеет диагональный вид

.

4. Выяснить, приводится ли к диагональному виду матрица

.

Решение. Аналогично примеру 2 находим, что данная матрица имеет собственные значения и отвечающие им собственные векторы и , где и . Матрица задана в пространстве размерности 3, но имеет два различных собственных значения. При этом все собственные векторы, отвечающие собственному значению , являются линейно зависимыми, так как соответствующая фундаментальная система решений состоит только из одного вектора. Следовательно, для матрицы нельзя выделить базис из трех собственных векторов, поэтому матрица не может быть приведена к диагональному виду.

Практическое занятие № 14