Матрица линейного оператора

Пусть - базис линейного пространства , в котором действует линейный оператор . Подействуем оператором на базисные векторы и разложим образы базисных векторов 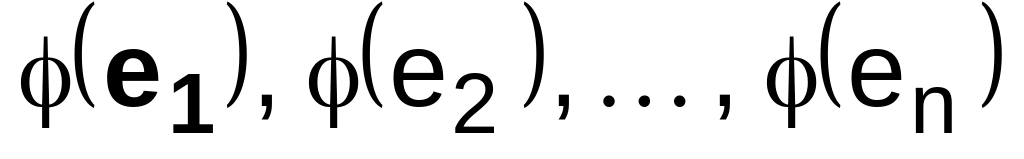по тому же базису:

Матрицей линейного оператора φ в базисе В =  называется квадратная матрица n-го порядка , i -тый столбец которой состоит из координат вектора в базисе , т.е.

.

Пусть ,а . Тогда связь между вектором и его образом выражается формулой

или (1)

Теорема 1 (связь между матрицами линейного оператора в разных базисах).

Пусть в линейном пространстве L выбраны два базиса и , причем в базисе линейный оператор имеет матрицу , а в базисе - матрицу . Тогда матрицы и связаны соотношением

(2)

где - матрица перехода от старого базиса к новому базису .

Операторы , действующие в линейном пространстве , называются равными, если для любого вектора хL: .

Если операторы равны, то и равны их матрицы в любом базисе. Верно и обратное. Поэтому если в линейном пространстве фиксирован базис , то между операторами, действующими в этом пространстве, и квадратными матрицами n-го порядка существует взаимно однозначное соответствие: каждому оператору соответствует матрица и, обратно, каждой матрице соответствует (и притом только один) оператор такой, что его матрица в базисе равна матрице .

Действия над линейными операторами

Пусть в линейном пространстве действуют два линейных оператора .

Суммой линейных операторов называется оператор , действие которого на любой вектор хL задается равенством

Сумма линейных операторов является линейным оператором, а матрица суммы линейных операторов (в любом базисе) равна сумме матриц этих операторов, т.е.

Произведением линейного оператора на число R называется оператор , действие которого на любой вектор хL задается равенством

Произведение линейного оператора на число является линейным оператором, а матрица произведения этого оператора (в любом базисе) равна произведению матрицы оператора на число , т.е.

Теорема 2. Множество всех линейных операторов, действующих в линейном пространстве , с введенными операциями сложения операторов, и умножения оператора на число образует линейное пространство.

Произведением линейных операторов называется оператор , действие которого на любой вектор хL задается равенством

Произведение линейных операторов является линейным оператором, а матрица этого оператора (в любом базисе) равна произведению матриц операторов , т.е.

Свойства операции умножения операторов

Для любого числа и для любых линейных операторов :

1)  3) 

2)  4) 

5)

Определение8.Линейный оператор называется обратным к линейному оператору , если выполняются равенства

где - тождественный оператор.

Теорема 3.

Для того чтобы существовал обратный оператор к линейному оператору , необходимо и достаточно, чтобы матрица оператора в каком-нибудь базисе была невырожденной (при этом она будет невырожденной в любом другом базисе).

Если - матрица оператора в базисе , то матрица обратного оператора в том же базисе равна , т.е. является обратной по отношению к матрице .

Решение типовых примеров и задач

1. Выяснить, является ли оператор линейным, если вектор

Решение. Пусть  , а   

Тогда , .

По определению операций над векторами:

, .

Найдем образы векторов и :

;

(х).

Так как и , то оператор является линейным.

2. Найти матрицу линейного оператора 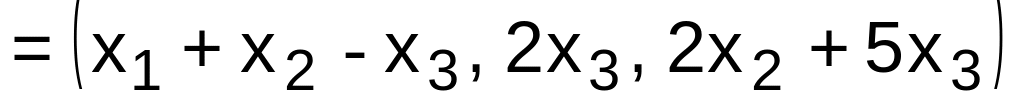, где , в том базисе, в котором даны координаты векторов .

Решение. Выразим связь между координатами вектора образа и вектора прообраза :

Пусть Х= , , . Тогда в матричной форме последняя система имеет вид

или ,

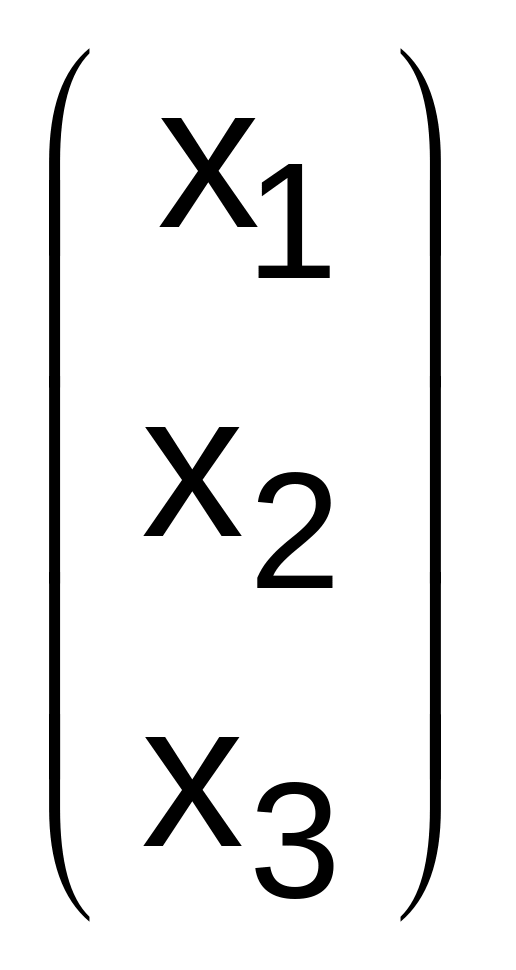откуда следует, что матрица оператора определяется как .

3. В пространстве действует линейный оператор , заданный в базисе матрицей

Найти координаты образа вектора и координаты прообраза вектора

Решение. а) Найдем координаты образа вектора , используя формулу (1):

б) Найдем координаты прообраза вектора по той же формуле (1):

Решив последнюю систему, получим х₁=0, х₂=0, х₃=1, т.е. .

4. Матрица линейного оператора в базисе имеет вид

Найти матрицу этого оператора в базисе , если

Решение. Воспользуемся формулой (2):

где - матрица перехода от базиса к базису В^/ (см.пр.зан.№10):

Найдем матрицу , обратную для матрицы (см.пр.зан.№3):

Тогда по формуле (2) получим:

5. Пусть оператор в базисе имеет матрицу , а оператор в базисе , где имеет матрицу . Найти матрицы операторов и в базисе .

Решение. По определению

и ,

где и - матрицы операторов и в базисе В соответственно. По условию .

Найдем матрицу А_ оператора в базисе В по формуле (2):

где - матрица перехода от базиса к базису В.

По условию

.

Следовательно,

.

Тогда

; .

Практическое занятие № 13