Линейные модели обмена

Цель: рассмотреть применение аппарата линейной алгебры для анализа микроэкономических моделей на примере простой модели обмена и модели международной торговли.

Литература

[1]/ глава 3, § 3.9. [3]/ глава 16, §16.3.

[2]/ глава 5, § 4. [5]/ глава 3, § 3.5.

[19]/ глава 3, § 3.6.

Справочный материал

Простая модель обмена

Пусть имеется система n отраслей производства , каждая из которых выпускает продукцию одного вида. Примем за единицу объем продукции каждой отрасли в рассматриваемом периоде. Обозначим через долю продукции отрасли , которая поступает в отрасль . Будем считать, что обмен продукцией происходит только внутри системы (система замкнута), т.е.

(1)

Рассмотрим матрицу коэффициентов :

где

Матрица А со свойством (1), в силу которого сумма элементов ее любого столбца равна единице, называется матрицей обмена.

Требуется установить такие цены на продукцию каждой отрасли, при которых вся система находится в равновесии, т.е. ни одна отрасль не обогащается за счет другой.

Пусть - цена одной единицы продукции отрасли , а x  - вектор цен. Тогда расход отрасли , т.е. стоимость всей закупаемой ею продукции, определяется как

Чтобы отрасль могла развиваться, ее расход не должен превышать дохода, который равен стоимости произведенной ею продукции, т.е. :

(2)

Если искомые равновесные цены существуют, то система неравенств (2) выполняется для них как система равенств:

(3)

Если вектор цен х представить в виде матрицы 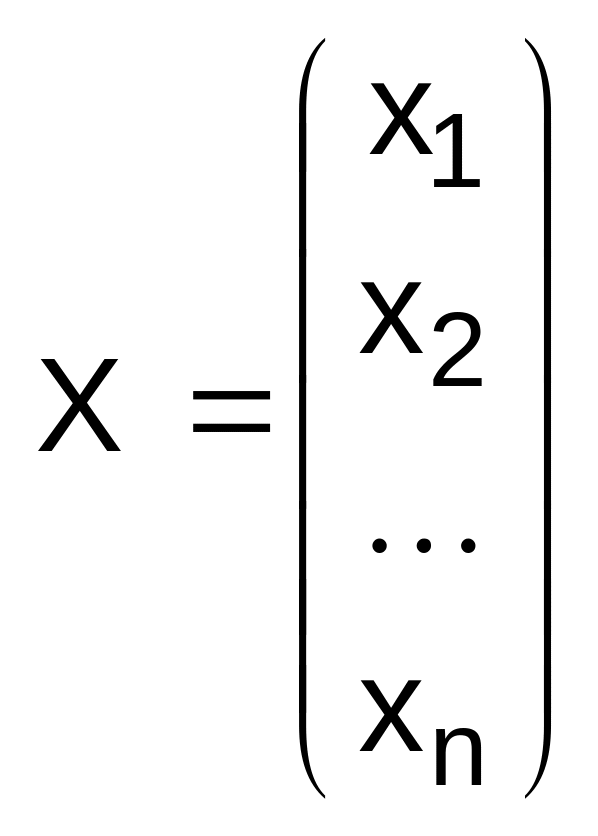, то систему (3) можно записать в матричной форме

(4)

Матричное уравнение (4) означает, что собственный вектор матрицы обмена А, отвечающий ее собственному значению , представляет собой искомый вектор равновесных цен.

Уравнение (4) можно переписать в виде, позволяющем определить Х:

.

Модель международной торговли

Пусть имеется система n стран , бюджет каждой из которых равен соответственно . Обозначим через долю бюджета , которую страна тратит на закупку товаров у страны . Будем считать, что весь бюджет расходуется на закупку товаров либо внутри страны, либо на импорт из других стран (система замкнута), т.е.

(5)

Рассмотрим матрицу коэффициентов :

где

Матрица А со свойством (5) называется структурной матрицей торговли.

Требуется найти вектор бюджетов стран x  , обеспечивающий равновесие всей системы, при котором отсутствует значительный дефицит торгового баланса для каждой из стран - участниц.

Для любой страны выручка от внешней и внутренней торговли определяется как

Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е.

(6)

Если искомые бездефицитные бюджеты существуют, то система неравенств (6) выполняется для них как система равенств:

Данную систему можно записать в матричной форме

или , (7)

где . Матричное уравнение (7) означает, что собственный вектор структурной матрицы торговли А, отвечающий ее собственному значению , состоит из бюджетов стран бездефицитной международной торговли.

Решение типовых задач

1. Экономическая система состоит из трех отраслей производства, каждая из которых выпускает один вид продукции. Обмен внутри системы происходит в соответствии с данной матрицей обмена

.

Найти вектор равновесных цен.

Решение.Найдем собственный вектор x  , отвечающий ее собственному значению , решив уравнение , которое в нашем случае имеет вид

.

В результате получим однородную систему линейных уравнений:

	х1	х2	х3
Х	33	32	28

Решив ее, найдем:  , т.е.  фундаментальная система решений имеет вид

.

Следовательно, х . Полагая  находим равновесные цены на продукцию каждой отрасли: , где с можно трактовать как множитель связанный с денежной единицей.

2. Структурная матрица торговли трех стран имеет вид .Найти соотношение бюджетов этих стран для сбалансированной торговли.

Решение.Найдем собственный вектор x  , отвечающий ее собственному значению , решив уравнение , которое в нашем случае имеет вид

.

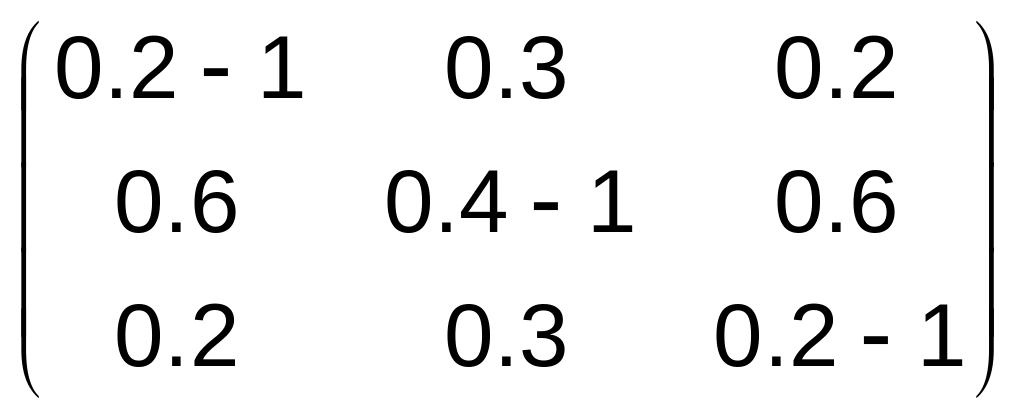В результате получим однородную систему линейных уравнений:

Решив ее, найдем:  , т.е.  фундаментальная система решений имеет вид

	х1	х2	х3
Х	1	2	1

.

Следовательно, х . Полученный результат означает, что при  бюджеты стран определяются как и сбалансированность торговли трех стран достигается при следующем соотношении их бюджетов:

.

3. Структурная матрица торговли четырех стран имеет вид . Найти бюджеты этих стран, удовлетворяющие сбалансированной торговли при условии, что сумма бюджетов задана:

Решение.Найдем собственный вектор x  , отвечающий собственному значению , решив уравнение , которое в нашем случае имеет вид

.

В результате получим однородную систему линейных уравнений:

Решив данную систему получим, что х

Следовательно, при  соответствующие бюджеты стран определяются как , х₂=146С,

Подставив найденные значения в заданную систему бюджетов, получим

,

откуда с=10.

Окончательно находим искомые величины стран при бездефицитной торговли (в условных денежных единицах):