3. Линейные пространства и операторы

3.1. Линейное пространство

Множество L элементов любой природы называется линейным или векторным пространством, если выполнены три условия:

1) задано сложение элементов L, т.е. закон, по которому любым элементам а,b L ставится в соответствие элемент c L, называемый суммой элементов a и b и обозначается с=а+b;

2) задано умножение элемента на число, т.е. закон, по которому любому элементу a L и любому числу αR ставится в соответствии элемент d L называемый произведением элемента а на (действительное) число α и обозначается d=αа;

3)указанные законы (линейные операции) подчиняются аксиомам линейного пространства.

Аксиомы линейного пространства

Аксиомы сложения.

1. Для любых а,b L: a+b=b+a (коммутативность).

2. Для любых a,b,c L: (a+b)+c=a+(b+c) (ассоциативность).

3. Существует элемент 0 L такой, что для любого a L: a+0=a (элемент 0 называется нулевым элементом).

4. Для любого a L существует элемент (-а) L такой, что а+(-а)=0 (элемент (-а) называется противоположным к элементу а).

Аксиомы умножения.

5. Для любого а L: 1·а=а.

6. Для любых α, β R, а L : α(βа)=(αβ)а.

Аксиомы, связывающие обе операции.

7. Для любых α,β R, а L: (α+β)a=αa+βa (дистрибутивность относительно суммы чисел).

8. Для любых а,b L, α R: α(a+b)=αa+αb (дистрибутивность относительно суммы элементов).

Элементы линейного пространства (множества L) называются векторами.

Определенное таким образом линейное пространство L называется действительным, так как введена операция умножения элементов множества L на действительные числа.

Пример 1. Выяснить, является ли линейным пространством множество квадратных матриц n-го порядка с действительными элементами.

Решение. Проверим выполнение условий определения1.

1)Сумма двух квадратных матриц n-го порядка есть матрица того же самого порядка (по определению сложения матриц).

2)Произведение квадратной матрицы n-го порядка на действительное число есть матрица того же самого порядка (по определению произведения матрицы на число).

3)Проверим выполнение аксиом линейного пространства. Пусть L – множество квадратных матриц n-го порядка. Очевидно, что для любых А, В, С L выполняются равенства:

А+В=В+А и (А+В)+С=А+(В+С),

т.е. аксиомы 1 и 2 выполнены.

Нулевым элементом является нулевая матрица n-го порядка

,

которая удовлетворяет аксиоме 3: для любой матрицы А L: А+0=А.

Противоположным элементом для любой матрицы

служит матрица

,

так же принадлежащая L, для которой выполнена аксиома 4: А+(-А)=0.

Выполняются и остальные аксиомы 5-8:

5) Для любой матрицы А L: Е·A=A, где Е – единичная матрица n-го порядка.

6) Для любых α, β R и А L: α(βА)=(αβ)А.

7) Для любых α,β R и (α+β)А=αА+αВ.

8) Для любых А, В L и α R: α(А+В)=αА+αВ.

Выполнение данных аксиом следует из свойств соответствующих операций над матрицами.

Таким образом, множество всех квадратных матриц n-го порядка с действительными элементами образует линейное пространство.

3.2. n-мерное векторное пространство

Упорядоченная совокупность n действительных чисел x_1,x₂,…,x_n называется n-мерным арифметическим вектором и обозначается х=( x_1,…,x_2,x_n), где x_i – i-тая компонента вектора x (i= ).

Два вектора x=(x_1,x_2,...,x_n) и y=(y_1,y_2,…,y_n) называются равными (х=у), если равны их соответствующие компоненты, т.е.

x₁=y₁, x₂=y_2,…,x_n=y_n.

Суммой двух векторов x=(x_1,x_2,…,x_n) и y=(y_1,y_2,…,y_n) называется вектор

z=x+y=(x₁+y_1, x₂+y_2,…,x_n+y_n).

Произведением вектора x на число α R называется вектор u=αx=(αx_1, αx_2,…,αx_n).

Вектор 0=(0,0,…,0) называется нулевым, а вектор –x=(-x_1, -x_2,…, -x_n) – противоположным к вектору x=(x_1,x_2,…,x_n).

Введенные операции сложения n-мерных векторов и умножение их на действительное число подчиняются аксиомам линейного пространства.

Множество всех n-мерных арифметических векторов, в котором определены указанные выше операции сложения векторов и умножения вектора на число, называется n-мерным арифметическим векторным пространством и обозначается Rⁿ.

Системой векторов линейного пространства L называется любая конечная последовательность элементов этого пространства.

Пусть задана система векторов

a_1,а_2,…,а_k (1)

линейного пространства L (а_iL, i= ).

Подсистемами данной системы векторов (1) называются сама эта система и любая система, получаемая из нее путем вычеркивания некоторых элементов.

Линейной комбинацией векторов (1) называется вектор а L, имеющий вид

а=α₁а₁+α₂а₂+…+α_ka_k= α_ia_i, (2)

где α1, α2,…, α_K– любые действительные числа.

При наличии равенства (2) говорят так же, что вектор а линейно выражается через векторы системы (1) или разлагается по этим векторам.

Пример 2. Найти все значения m, при которых вектор b=(1,m,3) линейно выражается через векторы а₁=(2,3,7), а₂=(3,-2,4), а₃=(-1,1,-1).

Решение. Вектор b линейно выражается через векторы а₁, а₂, а₃, если существуют числа α₁, α₂, α₃ такие, что

b=α₁а₁+α₂а₂+α₃а₃

или

α₁ α₂ +α_{3 .}

Перейдя к покомпонентным равенствам, получим систему:

Составим расширенную матрицу системы и преобразуем ее:

~ ~ ~ .

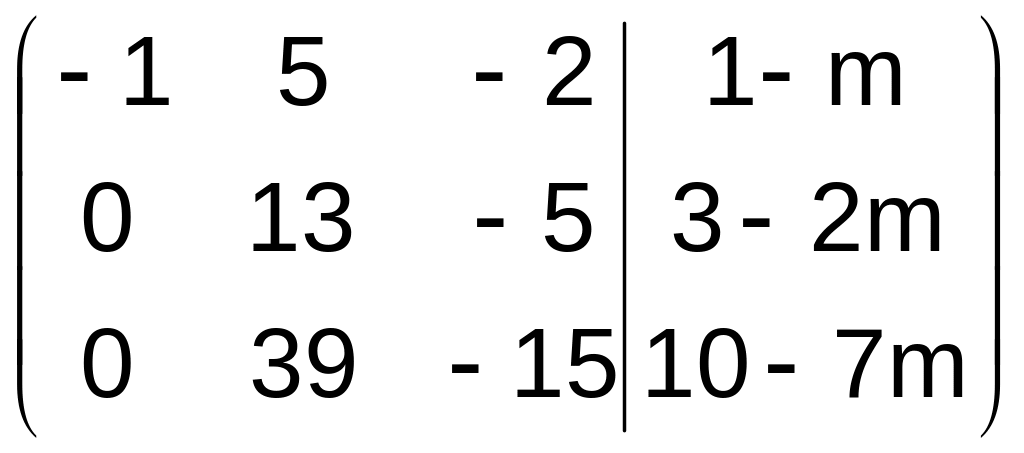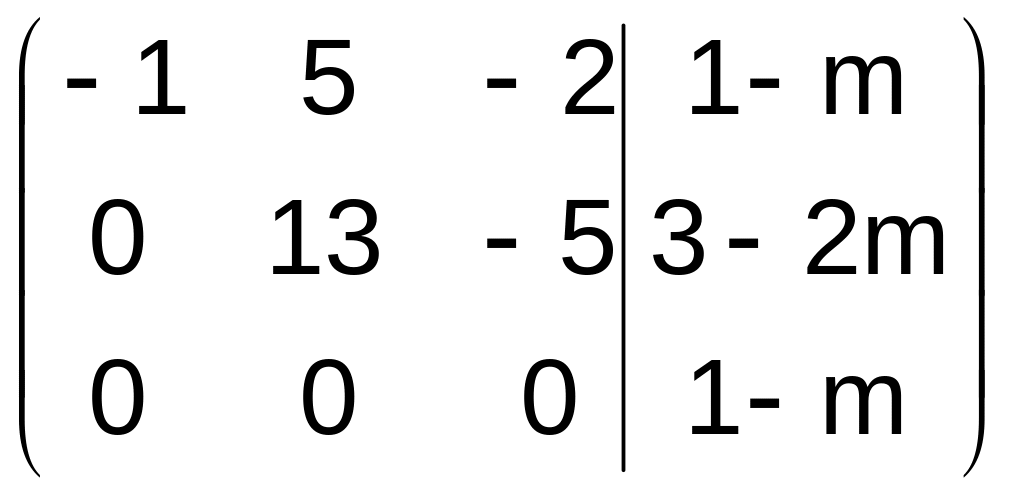Система является совместной, если ранг ее основной матрицы равен рангу расширенной матрицы. Это возможность только в том случае, когда 1-m=0, т.е. m=1. Следовательно, вектор b является линейной комбинацией векторов а₁, а₂, а₃ при m=1.

Cистема векторов (1) называется линейно зависимой, если существуют такие числа α_1, α_{2, …,} α_K R, не равные нулю одновременно, что

α₁а₁+α₂а₂+_…+α_kа_k=0 (3)

Если система векторов (1) такова, что равенство (3) возможно только при α₁=α₂=…=α_k=0, то это система называется линейно независимой.

Пример 3. Выяснить вопрос о линейной зависимости системы векторов: а₁=(1,-1,2,1), а₂=(1,-1,1,2),

а₃=(1,-1,4,-1).

Решение. Векторы а₁, а₂, а₃ линейно зависимы, если существуют такие числа α₁, α₂, α₃, из которых хотя бы одно отлично от нуля, что будет выполняться равенство

α₁а₁+α₂а₂+α₃а₃=0.

В последнее равенство вместо векторов а_1, а_2, а₃, 0 подставим их компоненты и перейдем к компонентным равенствам:

α₁ +α₂ +α₃ = .

Тогда получим систему

Решая последнюю систему методом Гаусса, приводим ее к виду:

Так как ранг системы (r=2) меньше числа неизвестных (n=3), то данная система имеет множество решений, в том числе и не нулевые решения. Следовательно, векторы а₁, а₂, а₃ линейно независимы.