1.4. Ранг матрицы

Пусть дана прямоугольная матрица размера : . Выделим в этой матрице произвольных столбцов, где ( “ка меньше либо равно меньшему из чисел или ”).

Определитель - го (“катого”) порядка, составленный из элементов матрицы , расположенных на пересечении выделенных строк и столбцов, называется минором - го порядка матрицы .

Элементы матрицы являются минорами 1-го порядка.

Рассмотрим всевозможные миноры матрицы , отличные от нуля.

Рангом матрицы называется наивысший порядок миноров данной матрицы, отличных от нуля.

Обозначение: или .

Свойства ранга матрицы:

1) если матрица имеет размеры , то ;

2) если все элементы матрицы равны нулю, то только в этом случае ;

3) если – квадратная матрица – го порядка, то только если .

Базисным называется минор, порядок которого определяет ранг матрицы.

У матрицы может быть несколько базисных миноров.

Если в матрице имеется минор – го (“эртого”) порядка, отличный от нуля, а все ее миноры – го (“эрплюспервого”) порядка, окаймляющие этот минор (то есть содержащие минор – го порядка целиком внутри себя), равны нулю, то ранг матрицы равен и данный минор – го порядка является базисным.

Алгоритм вычисления ранга матрицы методом окаймления миноров.

1. Найти ненулевой элемент матрицы (если такого нет, то ранг матрицы равен нулю).

2. Вычислить миноры второго порядка, которые окаймляют выбранный элемент.

3. Если среди вычисленных миноров второго порядка имеется отличный от нуля, необходимо рассмотреть все миноры третьего порядка, окаймляющие какой-нибудь минор второго порядка, не равный нулю. Продолжать так до тех пор, пока все миноры, окаймляющие ненулевой минор – го порядка не будут равны нулю. В этом случае ранг матрицы равен .

Пример 1. Найти ранг матрицы методом окаймления миноров .

Решение. Так как матрица содержит ненулевые элементы, то .

Матрица имеет миноры второго порядка отличные от нуля, например, . Следовательно, .

Вычислим миноры третьего порядка, окаймляющие минор :

;

;

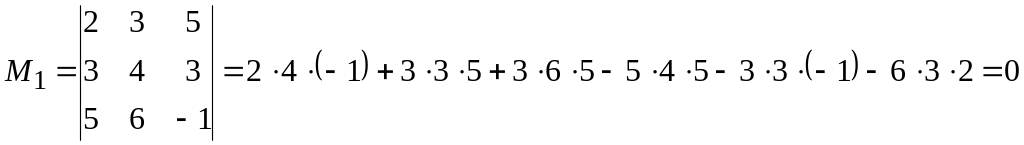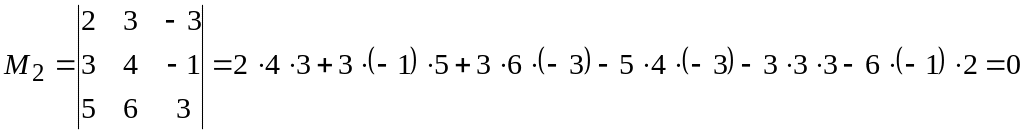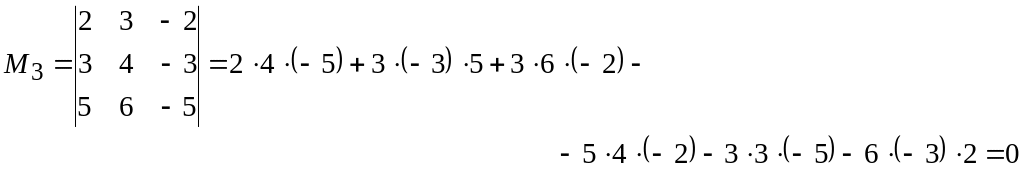
Так как все миноры третьего порядка, окаймляющие минор , равны нулю, то минор , имеющий второй порядок, является базисным минором матрицы и

Теорема (об элементарных преобразованиях матрицы). Элементарные преобразования строк или столбцов матрицы не изменяют ее ранг.

Из теоремы 1 следует, что если матрицы и эквивалентны ( ~ ), то

Ранг матрицы так же не меняется при ее транспонировании.

Ступенчатой называется матрица размера , если она имеет вид:

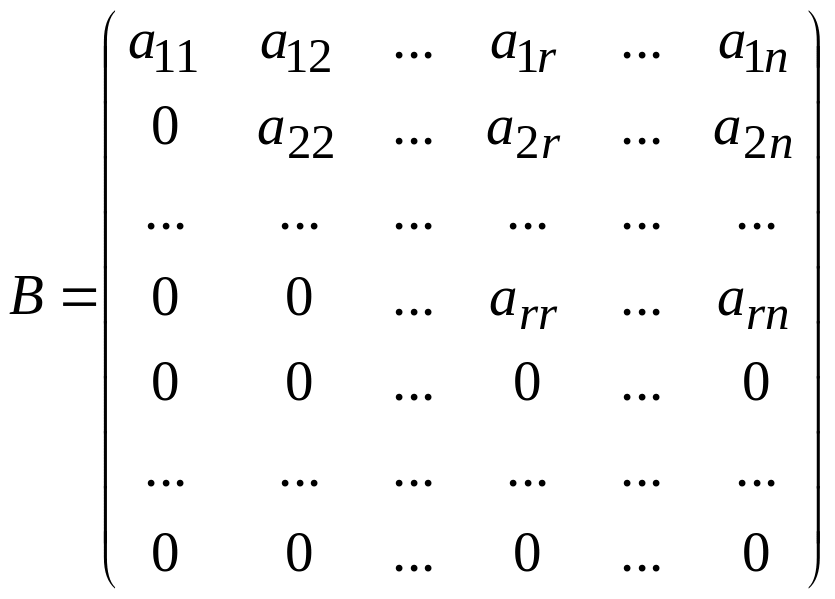, где отличны от нуля.

Любую ненулевую матрицу с помощью элементарных преобразований строк или столбцов можно привести к эквивалентной ей ступенчатой матрице .

Строка матрицы называется ненулевой, если хотя бы один ее элемент не равен нулю. Если все элементы строки равны нулю, то она называется нулевой.

Ранг ступенчатой матрицы равен числу ее ненулевых строк, то есть .

Алгоритм вычисления ранга матрицы с помощью элементарных преобразований.

1. С помощью элементарных преобразований привести матрицу к эквивалентной ей ступенчатой матрице .

2. Подсчитать число ненулевых строк в ступенчатой матрице . Тогда

Пример 2. Найти ранг матрицы c помощью элементарных преобразований .

Решение. Приведем матрицу к ступенчатому виду.

1. :

2. : =

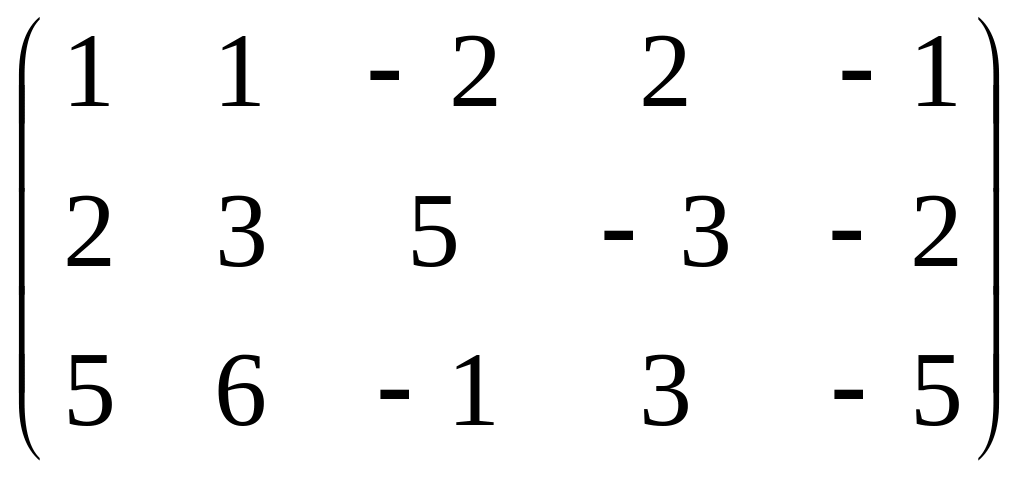
3. :

.

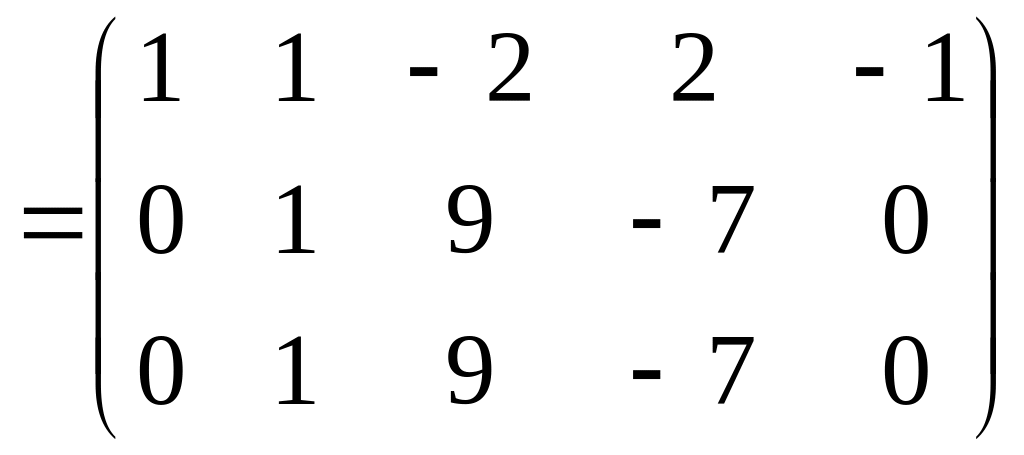4. Вычеркиваем все одинаковые строки кроме одной: .

Матрица приведена к ступенчатому виду, то есть, получена ступенчатая матрица эквивалентная матрице : ~ .
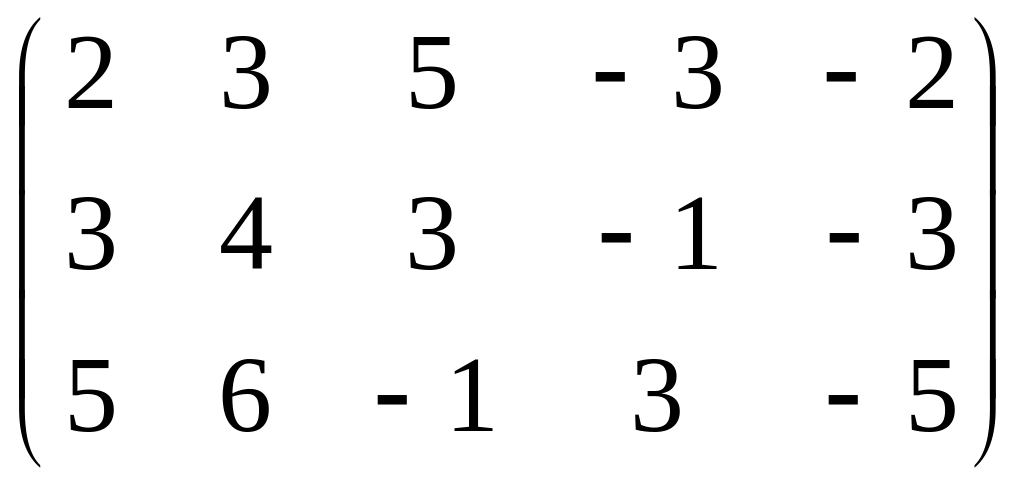