Линейная алгебра

1. Матрицы и определители

1.1. Матрицы и операции над ними

Матрицей называется прямоугольная таблица из (“эм на эн”) элементов некоторого множества: 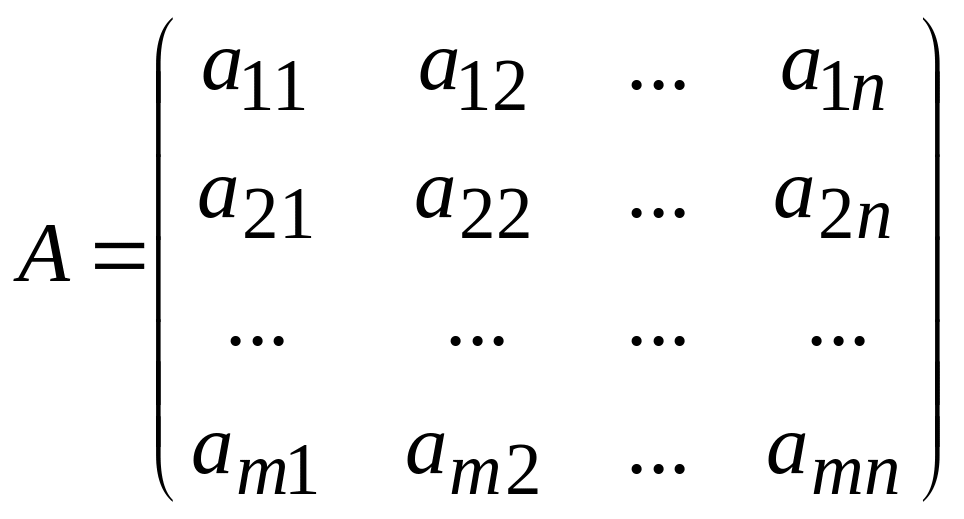. (1)

Числа, из которых составлена матрица, называются элементами матрицы.

Сокращенно матрица обозначается как ( , ).

Запись означает элемент матрицы, стоящий в - й (“итой”) строке ( ) и в - м (“житом”) столбце ( ).

В этом случае числа и называются индексами элемента, и они обозначают положение этого элемента в матрице. Первый индекс элемента матрицы указывает номер строки, второй – номер столбца.

Величина называется размерностью матрицы.

Матрица вида называется матрицей-строкой или просто строкой.

Матрица вида 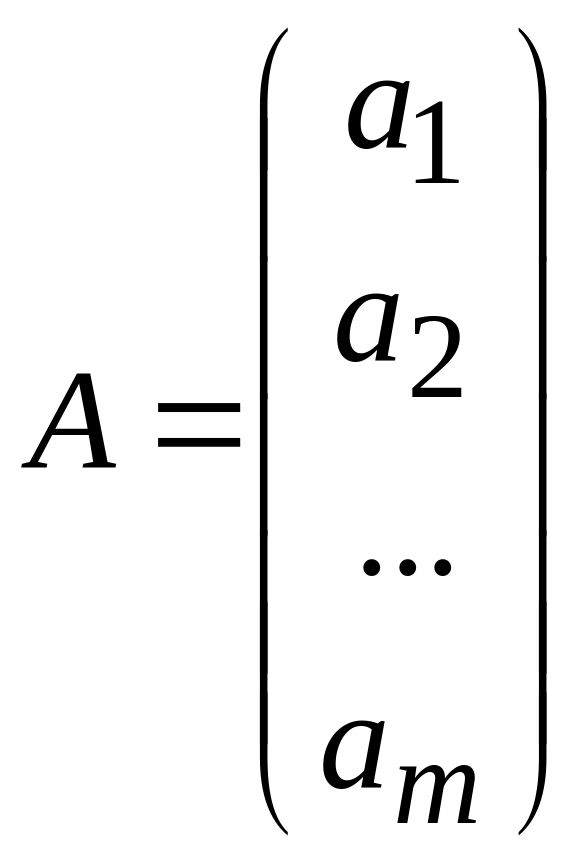называется матрицей-столбцом или просто столбцом.

Если в матрице одна строка и один столбец ( ), то она считается одноэлементной (представлена одним числом).

Если число строк и столбцов совпадают ( ), то матрица называется квадратной n-го (“энного”) порядка: 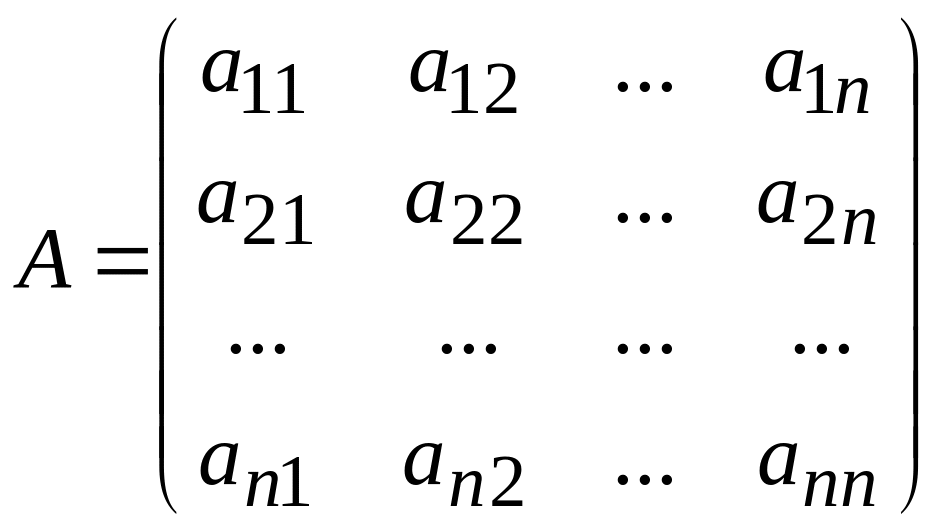. (2)

У квадратной матрицы есть две диагонали.

Элементы образуют главную диагональ, а элементы - побочную диагональ.

Пример 1. 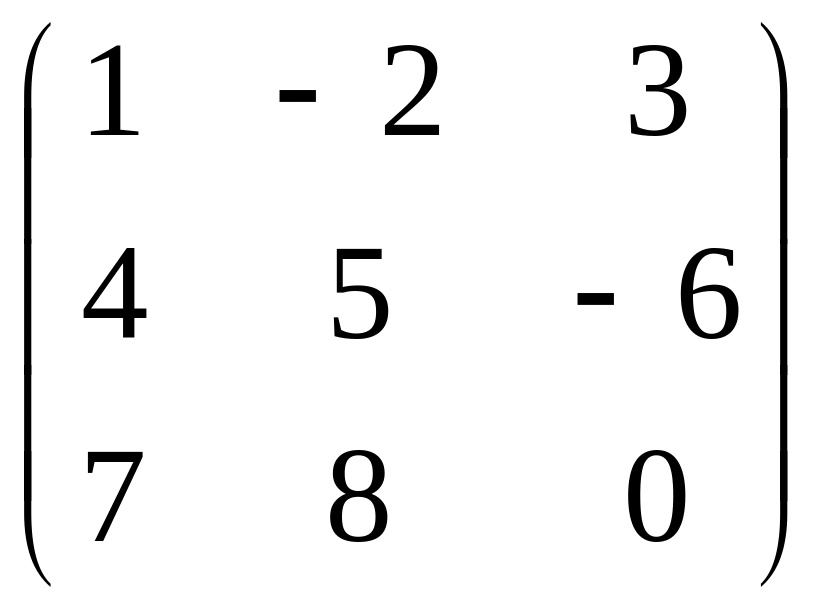- квадратная матрица 3-го порядка, - главная диагональ, - побочная диагональ.

Квадратная матрица (2) называется диагональной, если все элементы, не лежащие на главной диагонали, равны нулю: 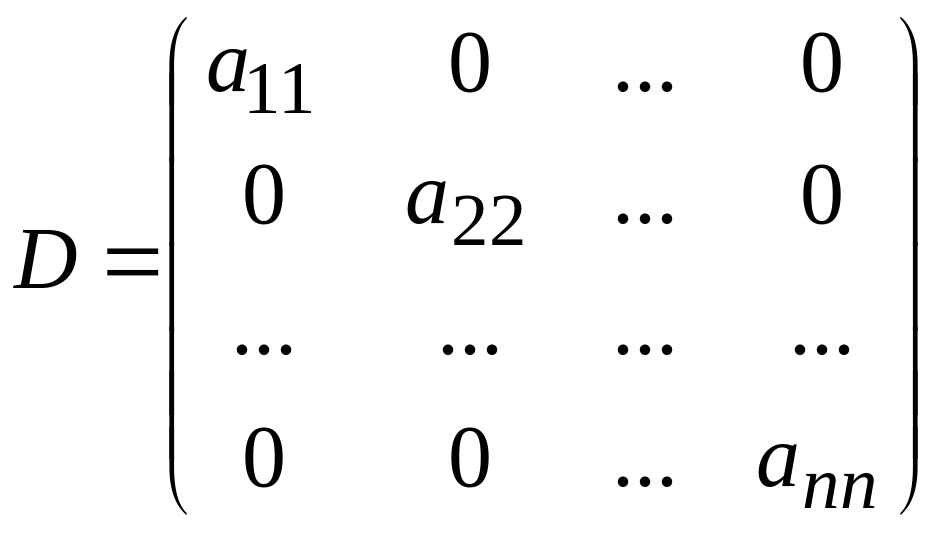. (3)

Пример 2. 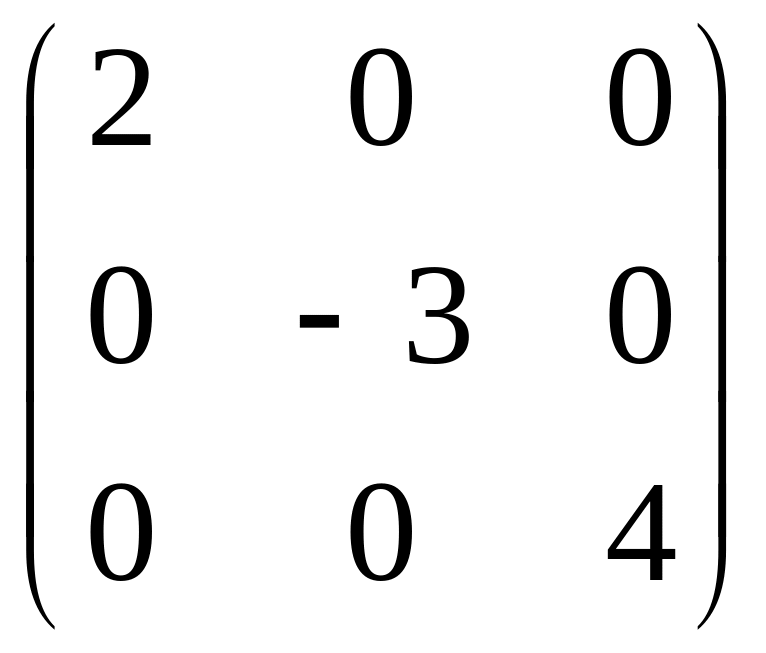- диагональная матрица.

Единичной называется диагональная матрица, все диагональные элементы которой равны единице (обозначается ): .

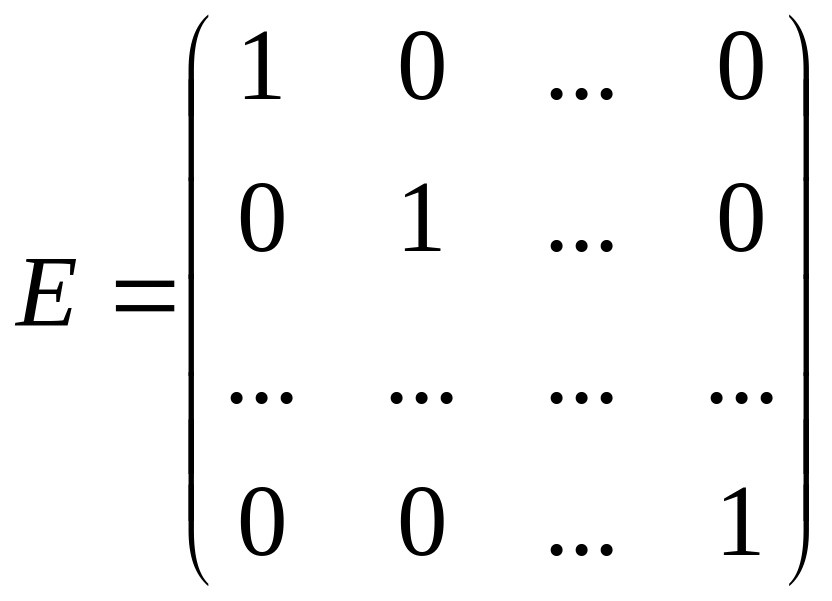Если в матрице все элементы равны нулю, то такая матрица называется нулевой, или нуль-матрицей и обозначается .

Две матрицы одинакового размера и называются равными ( ), если равны их соответствующие элементы, то есть для всех значений и .

Если в матрице поменять местами строки и столбцы (или для каждого элемента поменять местами индексы и ), то полученная матрица называется транспонированной и обозначается .

Пример 3. .

Матрица называется симметрической, если она не меняется при транспонировании, то есть .

Над матрицами можно выполнять следующие операции: сложение и вычитание матриц, умножение матрицы на число, умножение матриц.

Суммой двух матриц и называется матрица такая, что , где и .

Обозначение: .

Замечание 1. Сумма и разность существуют только для матриц одинакового размера.

Свойства операции сложения матриц:

1) (коммутативность сложения);

2) (ассоциативность сложения);

3) если – нулевая матрица того же порядка, что и матрица , то (нейтральный элемент относительно сложения).

Пример 4. .

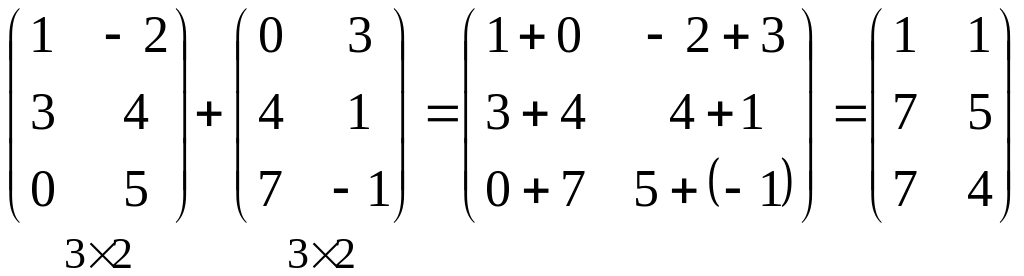Аналогично определяется разность двух матриц: , где , , .

Произведением матрицы на число (лямбда) называется матрица такая, что , где , .

Обозначение: .

Свойства операции умножения матрицы на число:

1) (мю);

2) ;

3) ;

4) ;

5) ;

6) .

Пример 5. .

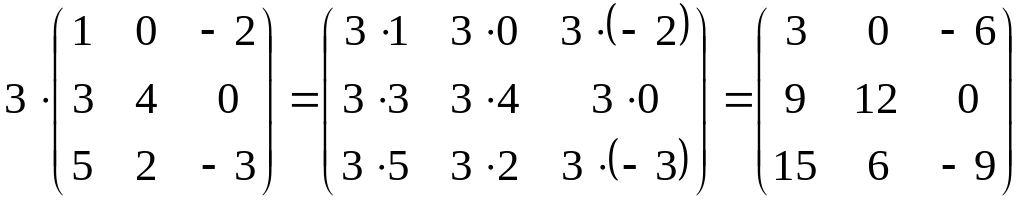Произведением матрицы на матрицу называется матрица , каждый элемент которой равен сумме произведений элементов -той строки матрицы на соответствующие элементы -го столбца матрицы , то есть , где и .

Обозначение: .

Замечание 2. Умножение допустимо, если число столбцов матрицы равно числу строк матрицы . При этом число строк матрицы будет равно числу строк матрицы , а число столбцов матрицы будет равно числу строк матрицы .

Свойства операции умножения матриц:

1) (в общем случае операция не коммутативна);

2) (ассоциативность);

3) (дистрибутивность);

4) (альфа);

5) .

Пример 6.

.

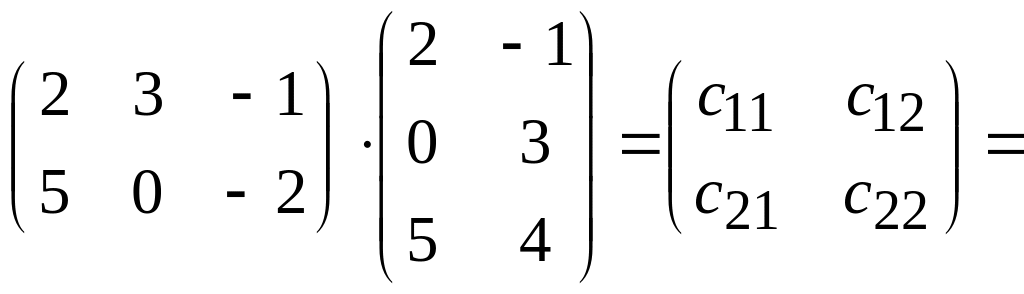
Если - целое неотрицательное число, тогда -й степенью квадратной матрицы называется матрица, которая вычисляется следующим образом: ; ; .