Абсолютно жесткий круглый и прямоугольный штампы.
Основное
условие решение задачи состоит в
равенстве перемещений точек штампа на
контактной поверхности при
.
Расчетная схема для определения
контактных напряжений под абсолютно
жестким штампом (рис. 4) приводит к
интегральному уравнению вида:
где
-
координаты центра элементарной
нагруженной площади
;
-
координаты рассматриваемой точки.
Решение этого уравнения для круглого штампа получено Штаерманом И.Я. в 1949 году и имеет вид:
где
а – радиус подошвы штампа до любой точки
контактной поверхности
.
Согласно этому решению в центре штампа
,
а при
.
В действительности в крайних точках
кругового штампа бесконечных напряжений
не возникает, так как напряжения
ограничены пределом прочности грунта.
Распределение контактных напряжений под прямоугольным штампом также можно определить из решения интегрального уравнения.
Приближенный метод решения такой задачи состоит в разбиении нагруженной площади на ряд элементов и замене интеграла на сумму:
где
n
– число элементов площади,
,
pi
–
неизвестное среднее давление площади
Fi
, причем
- расстояние центра
тяжести элемента от точки, для которой
составляется сумма W.
Контактные напряжения по подошве конструкций и сооружений конечной жесткости.
Не все конструкции можно рассматривать как абсолютно жесткие (штампы). Большинство конструкций и сооружений в результате взаимодействия со сжимаемым основанием испытывают деформации и прогибы, которые соизмеримы с прогибами контактирующей поверхности грунта основания. Жесткость таких конструкций и сооружений называется конечной, в отличие от бесконечно большой жесткости штампов. В связи с этим возникает ряд задач таких как:
- определение прогибов в конструкциях и сооружениях и сравнение их с допустимыми;
- определение внутренних усилий в элементах конструкций (эпюр поперечных сил и моментов) и оценка напряженного состояния материала конструкции;
- подбор армирования для гибких конструкций и оценка возможности трещинообразования.
Таким образом, определение эпюры контактных напряжений при взаимодействии конструкций и сооружений конечной жесткости и сжимаемого грунтового основания является основной задачей, решение которой открывает возможности для решения большого количества других актуальных задач. Сложность решения такой задачи заключается в том, что расчетные модели приходится формулировать в виде систем дифференциальных уравнений, решений которых сопряжено со значительными математическими трудностями.
ЛЕКЦИЯ 6. РАСЧЕТНЫЕ МОДЕЛИ И МЕТОДЫ РАСЧЕТА
СИСТЕМ «МАССИВ ГРУНТА – ФУНДАМЕНТНАЯ КОНСТРУКЦИЯ».
Расчетные модели оснований. Модель дискретной среды. Модель местных деформаций. Метод упругого полупространства. Однородное изотропное полупространство. Плоская задача теории упругости. Система «массив грунта – фундаментная конструкция».
Расчетные модели оснований.
Существует ряд моделей по-разному определяющих основные закономерности работы грунтового массива основания:
- модель дискретной среды;
- модель местных упругих деформаций;
- модель в виде полупространства (изотропное, анизотропное или с изменяющимися характеристиками по глубине);
- модель в виде слоя ограниченной толщины (или толщины и ширины);
Модель дискретной среды.
Модель дискретной среды применяется для крупнообломочных грунтов, для расчета напряженно-деформированного состояния каменно-набросных плотин и других элементов гидротехнических сооружений. Пример дискретной системы для плоской задачи в виде цилиндров приведен на рис. 1.
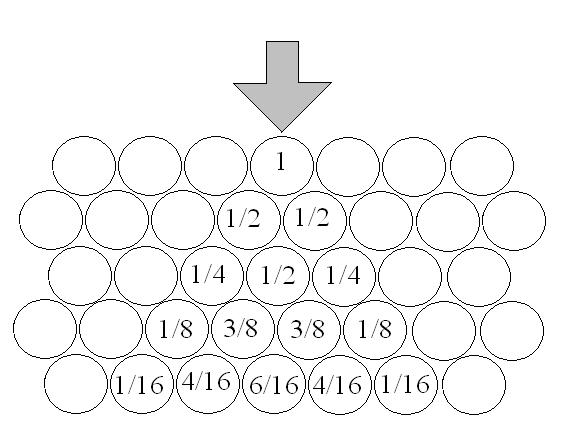
Рис. 1.
Наиболее простой является модель местных деформаций с одной характеристикой основания – коэффициенты постели.