ЛЕКЦИЯ 1. РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ

В ГРУНТОВОМ МАССИВЕ

Задача о действии одной сосредоточенной силы (задача Буссинеско), нескольких сил и любой распределенной нагрузки на плоское полупространство. Задача о действии местной равномерно распределенной на прямоугольной площади нагрузке (строгое решение А. Лява) и метод угловых точек. Эпюры сжимающих напряжений и влияние площади загрузки.

Задача о действии одной сосредоточенной силы

(задача Ж. Буссинеско)

Рассматривается действие сосредоточенной силы Р, приложенной перпендикулярно к ограничивающей полупространство плоскости. Полупространство однородно в глубину, в стороны и обладает линейной деформируемостью (рис. 1).

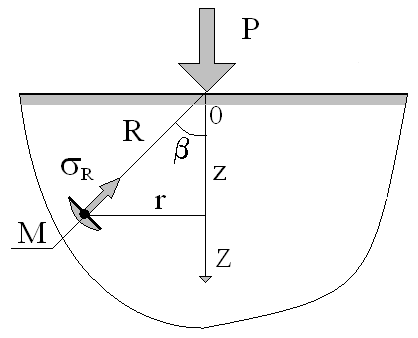
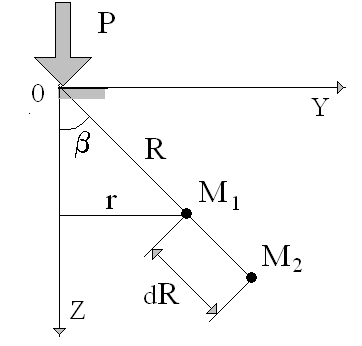
Рис. 1. Расчетная схема действия сосредоточенной силы

Для любой точки полупространства с координатами Z, Y или , R (например М₁ и М₂) перемещения точек по направлению радиуса R равно:

(1)

Относительная деформация грунта на отрезке dR :

(2)

Для линейно деформируемой среды напряжение пропорционально деформации

(3)

- коэффициенты пропорциональности.

Напряжения в массиве грунта связаны с величиной силы Р условиями равновесия. Для составления уравнения равновесия проведем полушаровое сечение с центром в точке приложения сосредоточенной силы (рис. 2).

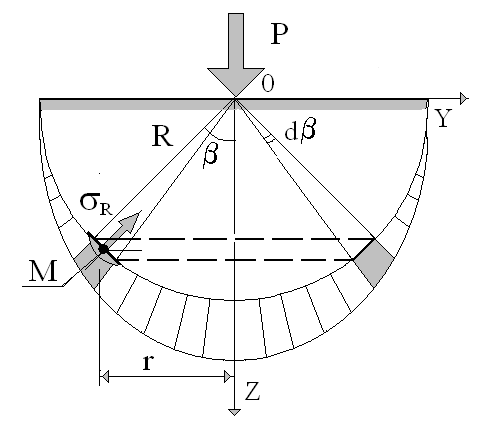
Рис. 2. Схема радиальных напряжений при действии сосредоточенной силы.

Для выделенного элементарного шарового пояса с центральным углом d радиальное напряжение принимается постоянным.

Условие равновесия – сумма проекций всех сил на вертикальную ось равна нулю:

(4)

dF – площадь кольца полушария при увеличении угла  на величину d:

(5)

Тогда:

(6)

После вычисления интеграла получим:

(7)

Отсюда следует, что

(8)

Поставляя найденные коэффициенты пропорциональности в (3) получим выражение для радиального напряжения

(9)

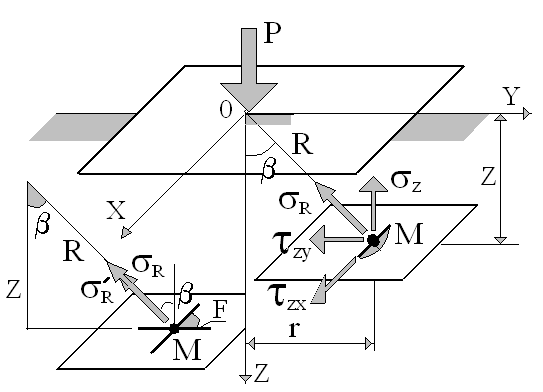
Рис. 3. Составляющие напряжений для площадки, параллельной ограничивающей плоскости.

Радиальное напряжение, отнесенное к площадке параллельной ограничивающей плоскости, обозначим . Из геометрических соотношений

(10)

Разложим силу на три направления z, x, y:

(11)

Учитывая, что

(12)

получим величины составляющих напряжений для площадки, параллельной ограничивающей плоскости:

(13)

Вывод: компоненты напряжений для площадок, параллельных ограничивающей полупространство плоскости, не зависят от упругих постоянных однородного линейно деформируемого полупространства.

Принимая во внимание, что

(14)

и обозначив

(15)

получим, широко используемое на практике при расчете осадок фундаментов простое выражение для сжимающих напряжений

(16)

Для облегчения расчетов значения коэффициента К сведены в таблицу [].

Рассмотрим действие сосредоточенной силы Q, приложенной на поверхности параллельно ограничивающей полупространство плоскости (рис.4.)

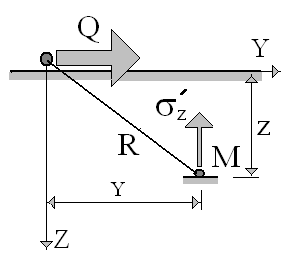
Рис. 4. Схема действия сосредоточенной силы Q.

Сжимающие напряжения при действии горизонтальной силы

(17)

Имея выражения для сжимающих напряжений при действии вертикальной и горизонтальной сил можно найти сжимающие напряжения ля наклонной силы.

Действие нескольких сосредоточенных сил на поверхности массива.

В основе определения суммарных напряжений от действия нескольких сосредоточенных сил, приложенных к поверхности массива (рис. 5), лежит гипотеза о прямой пропорциональности между напряжениями и деформациями, а также принцип суперпозиции

(18)

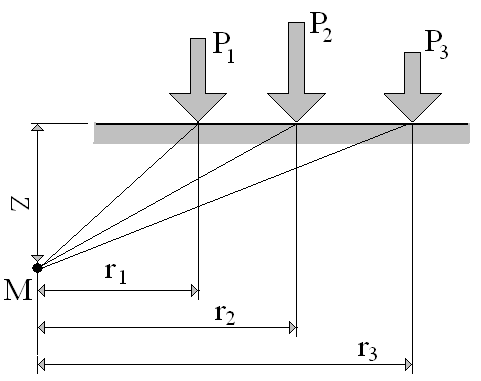
Рис.5 Схема действия нескольких сосредоточенных сил.

Действие любой распределенной нагрузки

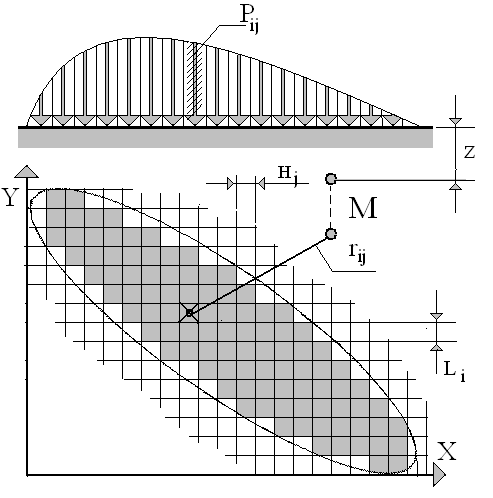
Рис. 6. Схема действия любой распределенной нагрузки.

(19)

(20)

Действие любой равномерно распределенной нагрузки

Для равномерно распределенной нагрузки в 1935 году А. Лявом получено строгое решение в случае прямоугольной площади загрузки. Деформации этой площади соответствуют деформациям поверхности линейно деформируемого пространства (Рис. 7).

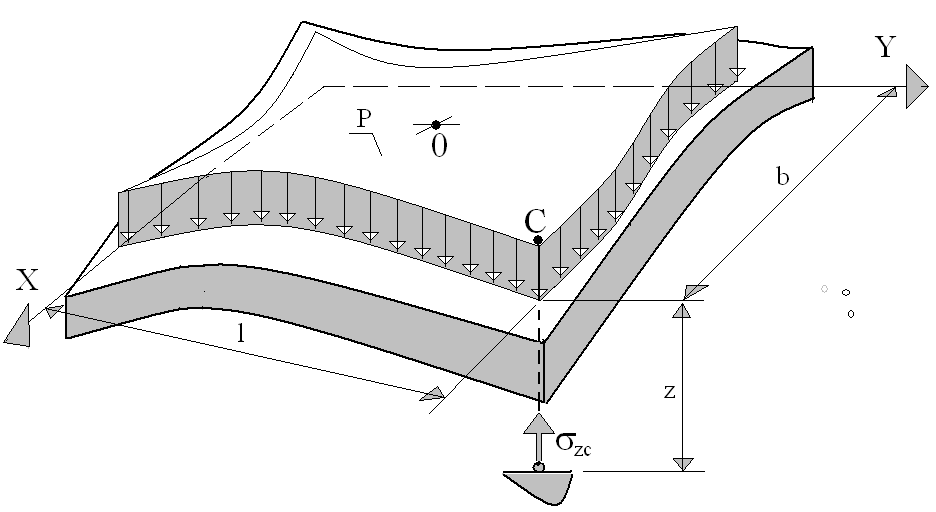
Рис. 7.

Это условие реализуется для очень гибкой передачи нагрузки.

Строгое решение получено для угловой точки C области нагружения

(21)

где .

Метод угловых точек

Полученное решение (21) позволяет определить сжимающие напряжения под центром площади (точка 0) и под углом (точка С) области загружения (Рис. 7)

(22)

Р – интенсивность равномерно распределенной нагрузки

Табличные коэффициенты: .

Используя различные схемы разбивки прямоугольной площади можно определить сжимающие напряжения для любой точки полупространства (Рис. 8)

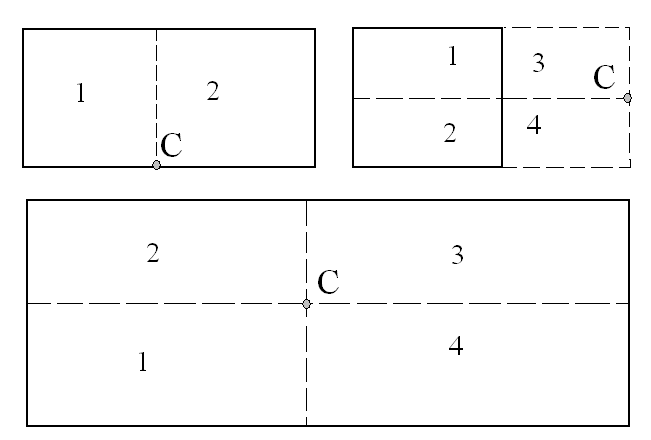
Рис. 8. Схемы разбивки прямоугольной площади в методе угловых точек

(23)

Эпюры сжимающих напряжений и влияние площади загрузки.

Эпюры в точке грунта основания от действия сосредоточенной силы (Рис. 9)

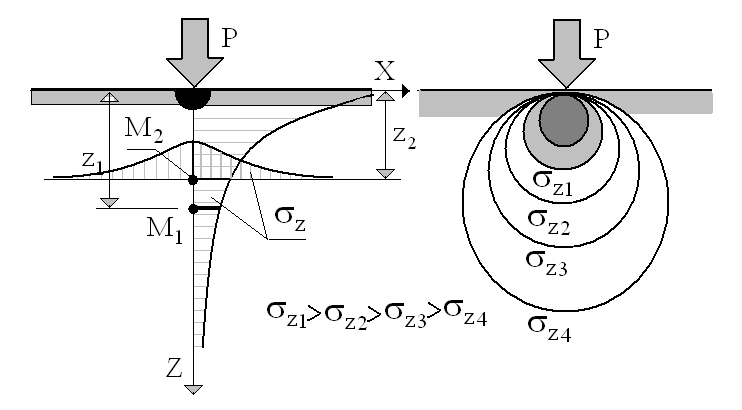
Рис. 9 Эпюры сжимающих напряжений и линий равных сжимающих напряжений при действии сосредоточенной силы

Влияние площади загрузки

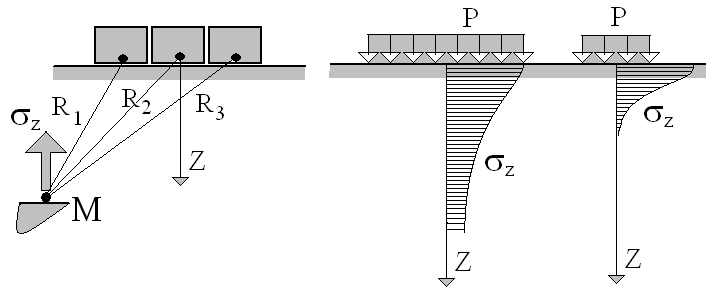
Рис. 10 Эпюры сжимающих напряжений при действии распределенной нагрузки

Площадь загрузки поверхности основания распределенной нагрузкой существенно влияет на скорость затухания сжимающих напряжений по глубине основания. Чем больше площадь загрузки поверхности основания, тем на большую глубину распространяются сжимающие напряжения.

Лекция 2. Деформации грунтов и расчет осадок фундаментов

Деформации грунтов оснований. Одномерная задача теории компрессионного уплотнения. Метод эквивалентного слоя. Метод послойного элементарного суммирования. Допущения метода послойного суммирования.

Деформации грунтов оснований.

Под влиянием особых условий, выражающихся в виде внешних воздействий на грунты основания строительной площадки, основание претерпевает деформации, которые подразделяются на два вида:

1. деформации от внешней нагрузки (осадки, просадки, горизонтальные смещения)

2. деформации от природных изменений и антропогенных воздействий (подъемы и опускания, оседания, горизонтальные смещения)

Осадки - это деформации уплотнения грунта, которые происходят в результате небольших вертикальных перемещений его твердых частиц, без коренного нарушения структурного строения и выдавливания грунта из-под фундамента. Грунт сжимается за счет уплотнения частиц. Это приводит к упрочнению и улучшению его строительных свойств. Для устойчивости и прочности оснований сжатие грунтов безопасно.

Просадки - это деформации, которые происходят в результате больших вертикальных перемещений частиц грунта с коренным изменением его структуры и часто сопровождается выдавливанием грунта из-под фундамента. Просадки развиваются не только от внешних нагрузок и собственного веса грунта, но и от дополнительных воздействий (деформации лессовых грунтов при замачивании, мерзлых грунтов при оттаивании ).

Горизонтальные деформации - сдвиг грунта - это значительные, необратимые наклонные и горизонтальные перемещения частиц грунта, когда горизонтальные составляющие напряжений превышают сопротивление грунтов сдвигу. Сдвиг грунта вызывается действием на основание горизонтальных и наклонных нагрузок. Сдвиг сопровождается изменением сложения грунта, перемещением отдельных больших объемов грунта, нарушением его сплошности, местной или общей потерей его устойчивости.

Подъемы и опускания - деформации связанные с изменениями объема некоторых грунтов при изменении их влажности (набухание или усадка) и при замерзании или оттаивании льда в порах грунта (морозное пучение или оттаивание).