Решение злп с помощью excel

L(x) = 130,5x₁ +20х₂ +56х₃ +87,8х₄ mах;

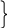-1,8х₁ +2x₂ + х₃ -4х₄ =756

- 6х₁ +2x₂ + 4х_з - х₄  450

4х₁ - 1,5х₂ + 10,4х₃ + 13х₄  89

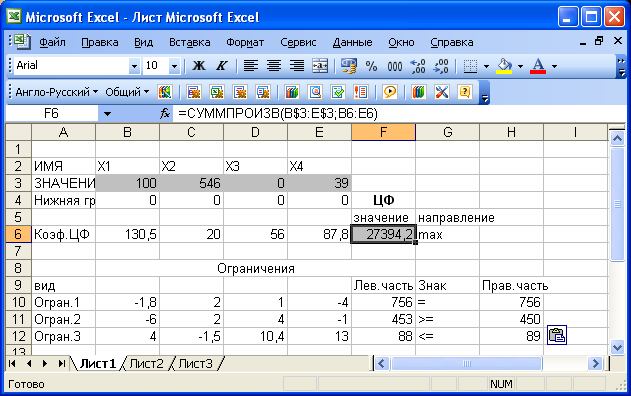
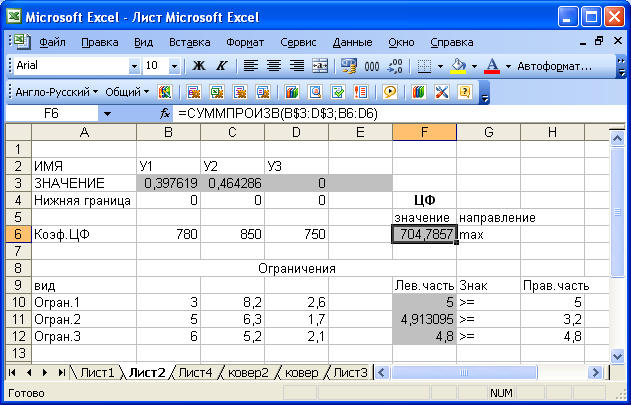
Введем значения из математической модели в экранную форму

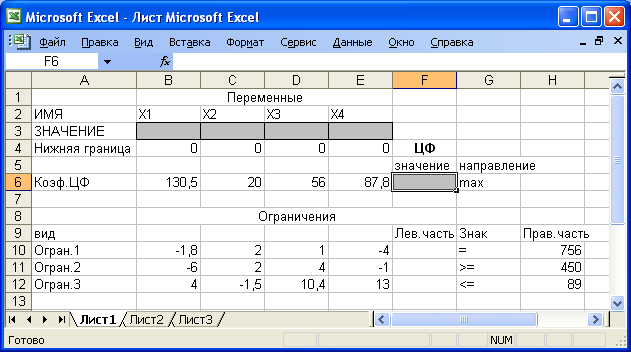
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано.

=СУММПРОИЗВ(В$3:Е$3;В6:Е6),

Формулы, описывающие ограничения модели

Левая часть ограничения	Формула Excel
-l,8x1 +2x2 +x3 - 4х4 или BIO* B3 + С10*СЗ+ D10*D3 + E10*E3	=СУММПРОИЗВ(В$3:Е$3;В10:Е10)
-6x1 +2x2 +4х3 -x4 или В11* ВЗ + СП*СЗ + D11*D3 +E11*E3	=СУММПРОИЗВ(В$3:Е$3;В11:Е11)
4x1 – 1,5х2 +10,4х3 +13x4 или В12*ВЗ+ С12*СЗ+D12*D3 + E12*E3	=СУММПРОИЗВ(В$3:Е$3;В12:Е12)

Экранная форма задачи после ввода всех необходимых формул

(курсор в ячейке F6)

Дальнейшие действия производятся в окне "Поиск решения", которое вызывается из меню "Сервис"

"Добавление ограничения"

Н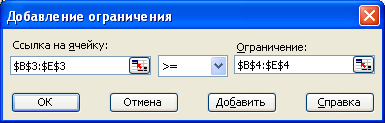 ажмите кнопку "Добавить", после чего появится окно

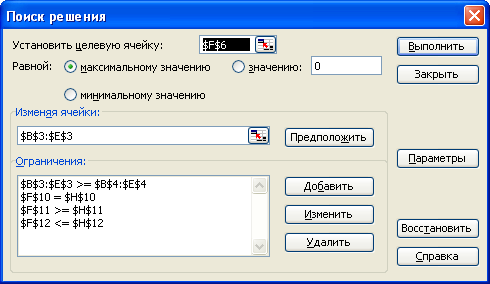
Окно "Поиск решения" после ввода всех необходимых данных задачи представлено на рис.

Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить".

ДВОЙСТВЕННАЯ ЗАДАЧА.

В 1975 году наш соотечественник Леонид Витальевич Канторович был удостоен Нобелевской премии по экономике за разработку теории оптимального использования ресурсов.

Каждой задаче линейного программирования соответствует другая задача, называемая двойственной или сопряжённой по отношению к прямой (исходной). Теория двойственности полезна для проведения качественных исследований ЗЛП.

Переменные двойственной задачи y_i называются двойственными оценками, «ценами» ресурсов, теневыми ценами.

Каждая задача двойственной пары фактически является самостоятельной ЗЛП и может быть решена независимо от другой.

Пример.

Цех выпускает три вида обувных картонов.

Производственные возможности цеха:

1. Суточный фонд рабочего времени оборудования – 780 ч,

2. Суточный расход сырья – 850 т,

3. Суточный расход электроэнергии – 750 кВт/ч

Нормы расхода производственных ресурсов на единицу различных видов картона представлены в таблице:

Ресурсы	Норма затрат на единицу продукции
	1	2	3
Оборудование, ч	3	5	6
Сырьё, т	8,2	6,3	5,2
Электроэнергия, кВт/ч	2,6	1,7	2,1

Прибыль от реализации 1т картона составляют: 1-го вида – 5руб., 2-го вида – 3,2 руб., 3-го вида – 4,8 руб.

Составить модель задачи плана производства продукции, обеспечивающего максимальную прибыль.

L(x)=5х₁+3,2х₂+4,8х₃max

3 х₁+5х₂ + 6х₃ 780

8,2х₁+6,3х₂+5,2х₃850

2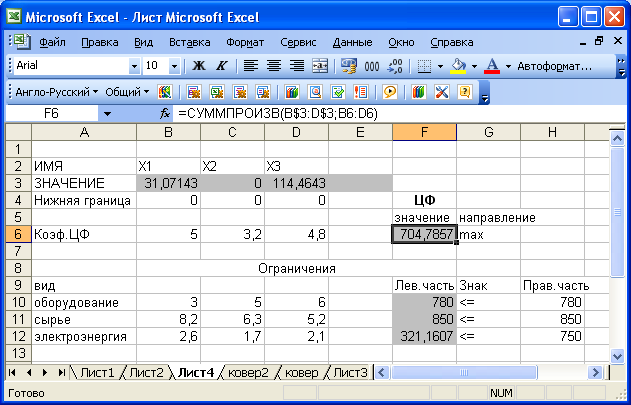 ,6х₁+1,7х₂+2,1х₃750

L_max=705 при х₁=31,07, х₂=0 и х₃= 114,5

Составляем двойственную задачу:

S(у)=780у₁+850у₂+750у₃ min

3 у₁+8,2у₂+2,6у₃5

5у₁+6,3у₂+1,7у₃3,2

6у₁+5,2у₂+2,1у₃4,8

Обе задачи обладают следующими свойствами:

1. В одной задаче ищут максимум линейной функции, в другой - минимум.

2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.

3. Каждая из задач задана в стандартной форме, причём в задаче максимизации – все неравенства вида «≤», а в задаче минимизации – все неравенства вида «≥».

4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.

Для задачи I А=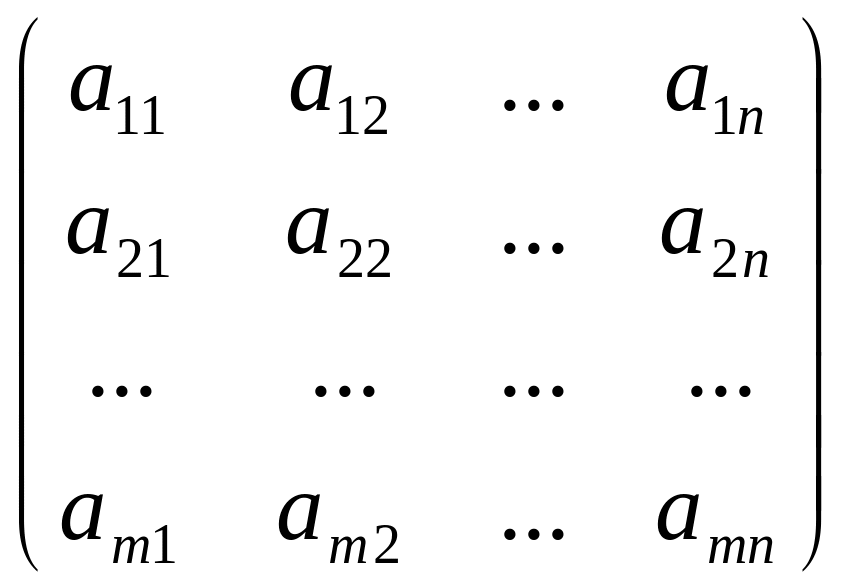 , для задачи II А=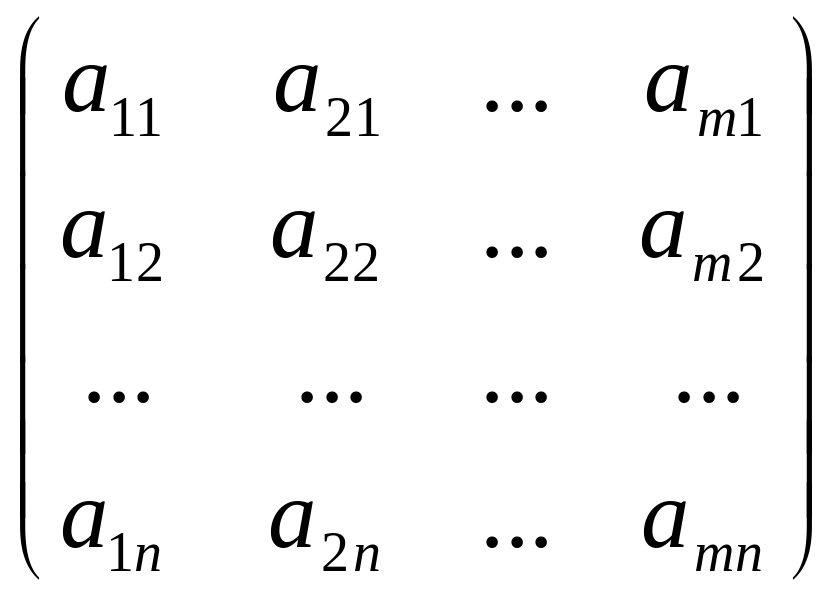

Т.е. левая часть ограничений определяет стоимость ресурсов, затраченных на производство единицы продукции.

5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.

6. Условия неотрицательности переменных имеются в обеих задачах.

Две задачи I и II линейного программирования, обладающие указанными свойствами, называются симметричными взаимодвойственными задачами.

Общая модель ЗЛП
Исходной (прямой)	Двойственной
L(x) = max при ограничениях (i = 1, 2,……,m) x j 0; j=1,2,….,n	S(y)=  min  сj yi 0

Первая (основная) теорема двойственности.

Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причём оптимальные значения их линейных функций равны:

F_max=S_min или F(X^*) =S(Y^*)

Экономический смысл первой теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить ли продукцию по оптимальному плану X^*=(x , x ,…, x ) и получать максимальную прибыль F_max либо продавать ресурсы по оптимальным ценам У^*=(у , у ,…, у ) и возместить от продажи равные ей минимальные затраты на ресурсы Z_min.

Вторая теорема двойственности (теорема о дополняющей нежесткости)

Пусть X=(x₁, x₂,…, x_n)- допустимое решение прямой задачи, а У=(у₁ у₂…, у_m)- допустимое значение двойственной задачи. Для того, чтобы они были оптимальными решениями соответственно прямой и двойственной задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:

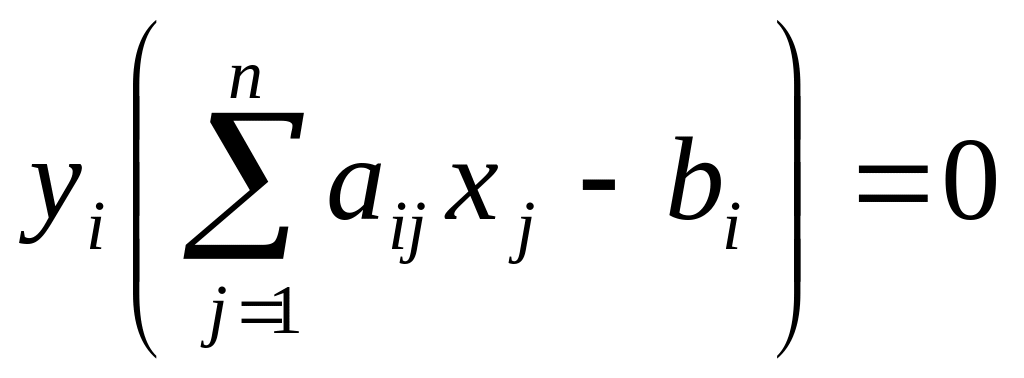
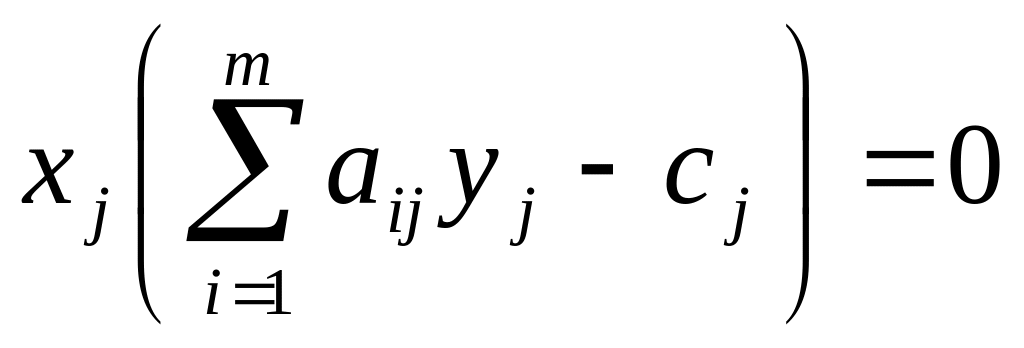
Эти условия позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи.

Цель?

1. Продать ресурсы.

2. Оценка дефицитности ресурса.

Если «у» = 0, то этот ресурс недефицитный (не из-за того, что его запас неограничен, а от того, что его невозможно использовать полностью в оптимальном плане)

3. Определение ценности ресурса.

• Чем больше «у», тем острее дефицитность ресурса и поэтому выгодно увеличивать именно его для увеличения прибыли.

• Ценность различных видов ресурсов нельзя приравнивать к действительным ценам. Речь идет о некоторой мере, имеющей экономическую природу, которая характеризует ценность ресурса только относительно полученного оптимального решения.

Двойственные задачи могут быть также несимметричные (= в ограничениях прямой задаче) и смешанными (=, ,)