Экспертное оценивание неформализуемых проблем производственных систем.

Экспертные методы представляют собой один из подходов к изучению сложных процессов и явлений, окончательное решение в сфере которых принимается субъективно.

Эти методы применяют когда:

1. невозможно предсказать и измерить последствия решений

2. доминируют качественные характеристики процесса

3. есть факторы, не поддающиеся контролю лицам, принимаемым решение

4. нужно принять решение в условиях неполноты исходной информации

5. отсутствуют надежные модели и невозможно формализовать изучаемый процесс

6. невозможно экспериментально проверить ход результатов прогнозирования

Экспертные методы применяют для:

1. выбора цели развития

2. прогнозирования

3. планирования

4. оценки качества продукции

5. классификации объектов

6. выбора вариантов решения

7. построения математических моделей

Методы: индивидуальные, групповые, коллективные

Способы получения информации от экспертов на основе:

• дискуссии

• анкетирования

• интервьюирования

• мозгового штурма

• совещания

• деловой игры

• смешанного подхода.

Экспертные оценки часто возникают на практике, например, при дегустации продуктов питания. Вообще они типичны для социологических опросов, например, менеджер по контролю качества проводит опрос покупателей в супермаркете. При использовании экспертного метода для оценки качества часто используется шкала порядка. Решается вопрос сравнения по принципу "лучше хуже", "больше меньше". Более подробная информация о том, во сколько раз лучше или хуже часто не требуется.

Количественные оценки: ранги, баллы, в долях

Ряд объектов, упорядоченных в соответствии со степенью проявления некоторого свойства, называют ранжированным; каждому числу такого ряда присваивается ранг. Будем обозначать ранги порядковыми числительными 1, 2, ..., n, где n-количество объектов. Таким образом, если какой-либо объект после ранжирования занимает третье место в ряду, ему присваивается ранг 3.

В условиях индивидуального эксперта ранг – основа принятия решения.

Метод экспертных оценок

В условиях групповой экспертной оценки (маркетинговые исследования) требуется проведение элементарных процедур обработки информации, полученной от экспертов. Вся информация, полученная от экспертов с целью принятия решений, независимо от вида в котором они представлены, подвергаются обработке.

Если 5£ эксперты £ 20, то 3£ объекты £ 7

Согласованность мнения экспертов можно оценивать по величине коэффициента конкордации (от лат. concordare - привести в соответствие, упорядочить) Кендалла:

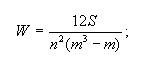
где S - сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего значения;

n - число экспертов;

m - число объектов экспертизы.

Коэффициент конкордации изменяется в диапазоне 0<W<1, причем 0 - полная несогласованность, 0,5- мнения экспертов в большей степени согласованы,1 - полное единодушие. Приемлемо, если ³ 0,33

Пример

Необходимо определить степень согласованности мнения пяти экспертов, результаты ранжирования которыми семи объектов приведены в таблице.

Номер объекта экспертизы	Оценка эксперта					Сумма рангов	Отклонение от среднего	Квадрат отклонения
	1	2	3	4	5
страна	4	6	4	4	3	21	1	1
дизайн	3	3	2	3	4	15	-5	25
цена	2	2	1	2	2	9	11	121
эксклюзив	6	5	6	5	6	28	8	64
состав	1	1	3	1	1	7	-13	169
бренд	5	4	5	6	5	25	5	25
универсальность	7	7	7	7	7	35	15	225
						140/20		630

Оцениваем среднеарифметическое число рангов:

= (21 + 15 + 9 + 28 + 7 + 25 + 35)/7 = 20.

Затем оцениваем сумму квадратов отклонений от среднего: S = 630. Определяем величину коэффициента конкордации:

W = 12 * 630 / 25 * (343 - 7) = 0,9

Полученный результат свидетельствует о достаточно высокой степени согласованности экспертов.

В том случае, если W<0,33 можно провести следующие действия:

• проанализировать состав экспертов и посмотреть мнения каких и почему выделяются из общей совокупности;

• посмотреть среднюю оценку и из рассмотренной совокупности оценок экспертов исключить мнения аномальных;

• процедура повторяется до тех пор пока W не будет ³ 0,33