4.4.Денормирование и расчёт элементов схемы фильтра.

Для перехода от нормированной схемы к денормированной схеме с заданными нагрузочным сопротивлением 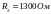и граничной частотой осуществляем изменение уровня сопротивления и масштаба частоты с помощью следующих множителей:

а) преобразующий множитель сопротивления:

.

б) преобразующий множитель частоты

Коэффициенты денормирования индуктивности и емкости определяем по формуле:

, .

Таким образом, истинные значения элементов фильтра можно определить как:

, , , , , , .

4.5Расчёт частотных характеристик фильтра

С помощью расчётачастотных характеристик фильтра проверяется соответствие фильтра техническим требованиям:

1. Рабочее ослабление в ПП не должно превышать заданной величины :

2. Рабочее ослабление в ПН не должно быть ниже заданного значения :

3. Рабочая фаза B(f) позволяет судить о выполнении требований к её линейности в пределах ПП.

Выполним расчёт частотных характеристик A(f) и B(f) по аппроксимированной функции H(p). Построим графики А(f) и B(f) ФHЧ.

Ω	0	0,259	0,5	0,707	0,866	0,966	1	1,4565
f (кГц)	0	2,382	4,6	6,504	7,967	8,88	9,2	13,4
А (дБ)	0,499	5,2·10-3	0,5	6,99·10-3	0,5	6,89·10-3	0,5	32,921
В (град)	0	73,32	145,49	-144,97	-80,51	-33,54	1,071	123,133

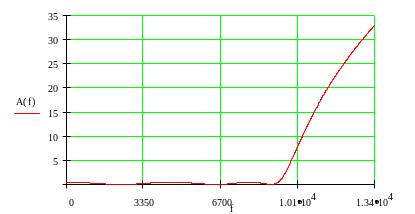
Рис. 9Графики зависимости рабочего ослабления ФНЧ

( ),

( ).

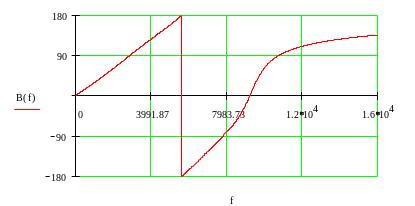
Рис. 10График зависимости рабочей фазы B(f) ФНЧ в ПП

Проверка технических требований по графикам зависимостей рабочего ослабления и рабочей фазы.подтверждает соответствие аппроксимированной передаточной функции H(р) техническому заданию. Это свидетельствует о правильности выполнения этапа аппроксимации

4.6 Расчет частотныххарактеристик фильтра на эвм.

После выполнения синтеза электрического фильтра важно убедиться в его соответствии техническим требованиям. Наиболее полной проверкой правильности расчета спроектированного фильтра является расчет частотных зависимостей и по передаточной функции Tp(j), выраженной через элементы фильтра.

Фильтр представляет собой реактивный четырехполюсник лестничной структуры. С учетом источника сигнала с внутренним сопротивлением R₁ и сопротивления нагрузки R₂

Рассчитаем и и сделаем проверку элементов схемы фильтра.

Рабочая передаточная функция такой схемы может быть определена следующим образом:

, где – комплексная частота.

, , .

Представим графики зависимости рабочего ослабления и рабочей фазы .

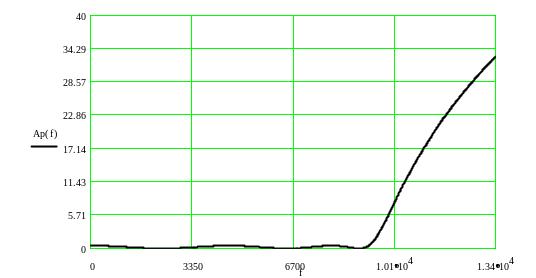
Рис.6Частотные зависимости рабочего ослабления

,

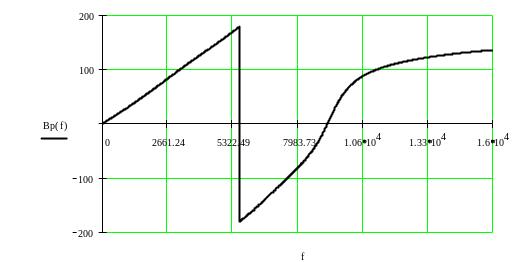
Рис. 7. Частотная зависимость рабочей фазы

4.7 Расчет временных характеристик фильтра на эвм.

Для расчета временных характеристик, например переходной характеристики h(t), необходимо получить операторное выражение этой характеристики

где Tu(p) – операторный коэффициент передачи по напряжению разработанного фильтра.

Um=1 B –амплитуда импульсов; fu=0.5*f2=4600 Гц –частота следования импульсов; q=N=T/τ=5 –скважиность импульсов; tu=1/N*fu=4,3*10^-5

Рассчитаем переходную характеристику:

Для вычисления переходной характеристики используем обратное преобразование Лапласа выражения

_{Построимграфикпереходнойхарактеристики}

Рисунок 8. График переходной характеристики h(t).

Рассчитаем отклик фильтра u(t) на прямоугольный импульс с амплитудой 1В и длительностью импульса

Рисунок 9. График зависимости выходного напряжения

Из графика (рис. 14) видно, что отклик фильтра на последовательность прямоугольных импульсов u(t) носит затухающий характер, а для одиночного прямоугольного импульса u(t-tu/2) – отклик описывает гармонические колебания равной амплитуды, имеющей небольшие искажения.