Основные термины

Абсолютно сходящимся называется знакочередующийся числовой ряд, соответствующий ряд из абсолютных величин которого сходится.

Бесконечно большой в точке называется функция, предел модуля которой в этой точке равен бесконечности.

Бесконечно малой в точке называется функция, предел которой в этой точке равен нулю.

Вторым замечательным пределом называется равенство вида .

Выпуклой вверх в точке называется функция , если в достаточно малой окрестности этой точки кривая, являющаяся графиком функции, лежит не выше касательной.

Выпуклой вниз в точке называется функция , если в достаточно малой окрестности этой точки кривая, являющаяся графиком функции, лежит не ниже касательной.

Гармоническим называется числовой ряд вида .

Геометрическим называется числовой ряд вида .

Геометрический смысл производной: производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке.

Дифференциалом функции называется главная часть приращения функции, линейная относительно приращения независимой переменной, то есть .

Дифференцируемой в точке называется функция , если ее приращение в этой точке можно представить в виде .

Знакочередующимся называется числовой ряд вида , где всегда .

Множеством называется некоторая совокупность объектов, рассматриваемых как единое целое.

Монотонной на промежутке называется убывающая или возрастающая на этом промежутке функция.

Неопределенностями называют функции, вопрос о существовании предела которых в некоторой точке нельзя решить на основании арифметических свойств пределов. Основными неопределенностями являются: .

Неопределенным интегралом функции на промежутке X называется совокупность всех первообразных функции, то есть .

Непрерывной в некоторой точке функцией называется функция, которая определена в окрестности этой точки и ее предел равен значению в ней, то есть .

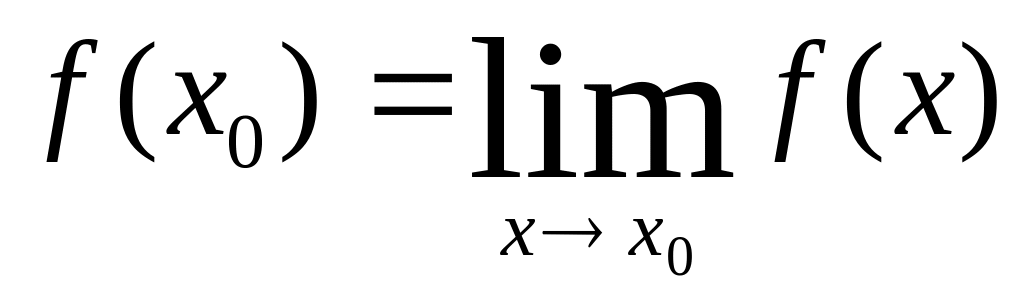Областью сходимости степенного ряда называется множество всех значений переменной , при которых соответствующий числовой ряд сходится.

Определенный интеграл: пусть предел интегральной суммы при стремлении длины наибольшего интервала разбиения отрезка к нулю существует, конечен и не зависит от способа разбиения и выбора точек ; тогда этот предел называется определенным интегралом функции на отрезке . При этом пишут: .

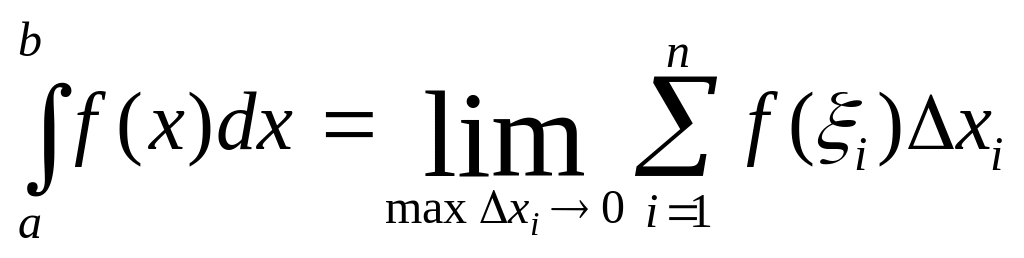Первообразной для функции на промежутке X называется функция такая, что при всех X выполняется равенство .

Первым замечательным пределом называется равенство вида .

Полным дифференциалом функции называется выражение вида .

Пределом функции при x, стремящемся к , называется число , если при всех значениях аргумента, достаточно близких к , соответствующие значения функции сколь угодно мало отличаются от , то есть: . При этом пишут: .

Пределом числовой последовательности называется число , если члены последовательности с достаточно большими номерами сколь угодно мало отличаются от , то есть . При этом пишут: .

Предельный анализ: применение дифференциального исчисления к исследованию экономических объектов и процессов на основе предельной выручки, предельного дохода, предельного продукта, предельной полезности, предельной производительности, которые с математической точки зрения являются производными соответствующих экономических функций.

Приращением аргумента называется выражение вида .

Приращением функции в точке называется выражение вида .

Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю, то есть .

Расходящейся называется числовая последовательность, предел которой равен бесконечности.

Расходящимся называется числовой ряд, предел последовательности частичных сумм которого бесконечен или не существует.

Степенным рядом называется ряд вида , где не зависит от .

Сходящейся числовой последовательностью называется числовая последовательность, если имеющая конечный предел.

Сходящимся называется числовой ряд, предел последовательности частичных сумм которого конечен.

Точкой перегиба графика функции называется точка , если в достаточно малой окрестности этой точки при точки графика функции лежат по одну сторону от касательной, а при - по другую от касательной.

Точкой разрыва второго рода функции называется точка , в проколотой окрестности которой функция определена и имеющая в ней хотя бы один бесконечный предел.

Точкой разрыва первого рода функции называется точка , в проколотой окрестности которой функция определена, но имеет в ней разные конечные пределы.

Точкой устранимого разрыва рода функции называется точка , в проколотой окрестности которой функция определена и имеющая в ней равные конечные пределы, не совпадающие со значением функции в точке .

Условно сходящимся называется знакочередующийся ряд, если он сходится, но не абсолютно.

Формула Ньютона – Лейбница вычисления определенного интеграла: , где - первообразная для подынтегральной функции.

Функцией называется соответствие между двумя множествами X и Y, при котором каждому элементу первого из них найдется, притом единственный, элемент второго: .

Функцией двух аргументов называется соответствие между двумя множествами и , при котором каждому элементу первого из них найдется, притом единственный, элемент второго: .

Частным дифференциалом функции двух переменных по переменной называется главная часть частного приращения функции по переменной . При этом .

Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю.

Числовой последовательностью называется функция, заданная на множестве натуральных чисел: .

Числовым рядом называется пара последовательностей вида , где . При этом последовательность , зависящая от , называется ее последовательностью частичных сумм.

Эластичностью функции называется предел отношения относительного приращения функции к относительному приращению аргумента при стремлении приращения аргумента к нулю, то есть .

Эквивалентными при называются бесконечно малые или бесконечно большие функции , если предел их отношения равен единице.

Экстремумами функции называются точки ее максимумов или минимумов.

Учебное издание

Авторы-составители:

Базанова Светлана Вениаминовна,

старший преподаватель кафедры естественнонаучных дисциплин и математики

Игнатьева Ирина Владимировна,

кандидат физико-математических наук, доцент

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Учебно-методическое пособие

для студентов заочной формы обучения

(квалификация (степень) «Бакалавр»)

Подписано в печать 23.01.2013

Формат 60×90¹/₁₆. Бумага SvetoCopy

Гарнитура Times New Roman. Печ. л. 1,5

Тираж 100 экз. Заказ № 35–12

Издательство ЧОУ ВПО «Института правоведения и предпринимательства»

(Санкт-Петербург)