2.3 Силовой анализ ведущего звена

Ведущее звено не является статистически определенным, так как для него . Для достижения равновесия в кривошипе необходимо положить дополнительную силу или момент сил. Эту силу условно называют уравновешивающей. Физический смысл этой силы заключается в том, что она приложена к кривошипу со стороны двигателя и является по сути дела движущей силой для рабочих машин. Для машин-двигателей эта сила будет являться силой сопротивления.

Определяем величину уравновешивающей силы:

Чтобы определить реакцию в шарнире , запишем векторное уравнение равновесия сил, приложенных к кривошипу:

Для построения плана сил берем прежний масштаб.

2.4 Определение уравновешивающей силы методом Н.Е.Жуковского

Искомая сила является замыкающей силой, то есть соединяющая конец вектора с началом вектора .

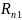Уравнение моментов всех сил относительно полюса плана скоростей Р

Расхождение результатов определения уравновешивающей силы методом Н.Е.Жуковского и методом построения планов сил не должна составлять более ±(5-7)%

3. Кинематический анализ и синтез зубчатого механизма

3.1 Определение геометрических размеров цилиндрической эвольвентной зубчатой передачи.

ДАНО:

- передаточное число.

Коэффициент высоты зуба рейки h=1

Коэффициент радиального зазора С=0,25

1. Угол зацепления зубчатой пары:

2. Определяем межосевое расстояние пары зубчатых колес:

3. Начальные диаметры:

4. Делительный диаметр:

5. Значение коэффициентов воспринимаемого смещения у и коэффициента уравнительного смещения ∆у:

6. Диаметр вершин зубьев:

7. Диаметры впадин зубчатых колес:

8. Диаметры основных колес:

9. Шаг окружной, основной

10. Шаг зубьев по начальной окружности:

11. Шаг зубьев по основной окружности:

мм

12.Угловой шаг:

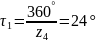
13.Толщина зуба по дуге делительной окружности:

14. Ширина впадин по дуге делительной окружности:

15. Углы профилей на окружностях выступов зубьев:

16. Вычисление толщины зубьев на окружностях вершин зубьев:

Необходимая ширина площади зуба на вершине:

S≥0,3m=0,6 мм

Следовательно, зубья обоих колес удовлетворяют условию отсутствия заострения.

Коэффициент перекрытия зубчатых колес:

Коэффициент перекрытия рассматриваемой пары зубчатых колес превышает минимальную допустимое значение:

Ɛ=1,14>1,1

3.2 Построение картины зубчатого зацепления нулевых колёс

Масштаб построения принимаем

Порядок построения картины зацепления:

1. На линии центров на межосевом расстоянии откладываем центры вращения колес. Из этих центров проводим начальные окружности обоих колес. Эти окружности будут кататься друг друга в точке Р- полюсе расстояние.

2. Через точку Р проводим общую касательную к начальным окружностям

и под углом зацепления проводим линию зацепления . Из центров опускаем перпендикуляры на линию . Длинны этих перпендикуляров равны радиусам основных окружностей.

3. Проводим основные окружности.

4. Принимая полюс Р линии зацепления за вычерчивающую точку и перекатываем производящую прямую по основным окружностям, строим эвольвенты верхней и нижней основных окружностей. Эти эвольвенты – профили зубьев соответствующих колес.

Для этого отрезок АР делим на равные отрезки (точки 1,2,3,4,А). Таки еже отрезки откладываем и влево от точки А. Основную окружность влево и вправо от точки касания А делим на такие же отрезки. При перекатывании производящей прямой по основной окружности точки 1,2,3… прямой совместятся с соответствующими точками 1,2,3… основной окружности, а сама прямая всякий раз будет касаться основной окружности.

Для более точного построения, касательные через точки 1,2,3… проводим в сторону Р перпендикулярно к соответствующим радиусам . Раствором циркуля, равным расстоянию от полюса зацепления Р до точки 1 по линии зацепления, из точки 1 на соответствующей касательной делаем засечку.

Затем раствором циркуля, равным расстоянию от полюса до точки 2, из точки 2 делаем засечку на соответствующей касательной и т.д. Через засечки проводим плавную кривую от основной окружности до окружности вершин зубьев, которая является эвольвентой, то есть профилем зуба.

Таким же образом вычерчиваем профиль зуба для второго колеса.

5.Откладываем по делительным окружностям дуги, равные толщине зубьев и ширине впадин . Делим толщину зуба пополам и проводим луч из центра вращения колеса через середину зуба, получаем ось симметрии зуба. Вторую симметричную половину профиля зуба вычерчиваем по шаблону. Затем откладываем от оси симметрии угловой шаг и строим профили остальных зубьев. 6. Определяем рабочий участок ав линии зацепления.

7. Определение дуги зацепления. Так как зацепление происходит на рабочем участке линии зацепления ав, то через точки а и в, соответствующие началу и концу зацепления, строим пунктиром один и тот же профиль зуба. Точки пересечения этих профилей с начальными окружностями соответствуют крайним точкам дуги зацепления первого колеса и второго.

8. Находим рабочие участки профилей зубьев, то есть те участки профилей, которые участвуют в зацеплении. Для этого через крайние точки рабочего участка линии зацепления а и в из центров проводим дуги до пересечения с профилем соответствующего зуба. Участки профилей зубьев, заключенные между проведенными дугами и окружностями выступов колес, икомые рабочие участки.