Геометрические и физические приложения двойного интеграла.
Пусть
G
– материальная пластинка (квадрируемая
фигура) на плоскости с плотностью
1.
Площадь пластины
2.
Масса пластины m=
3. Статические моменты пластинки относительно осей Ox и Oy
4.
Координаты центра тяжести пластинки
5. Моменты инерции пластинки относительно осей Ox и Oy
,
6. Момент инерции пластинки относительно начала координат
Пример: вычислить площадь пластины ограниченной линиями: y=x; y=0; y²-4y+x²=0; y²-8y+x²=0
Запишем уравнения линий, ограничивающих область интегрирования:
y²
- 4y
+ x²
=0 y
Окружность с центром, Окружность с центром,
сдвинутым по у на 4 единицы
сдвинутым по у на 2 единицы
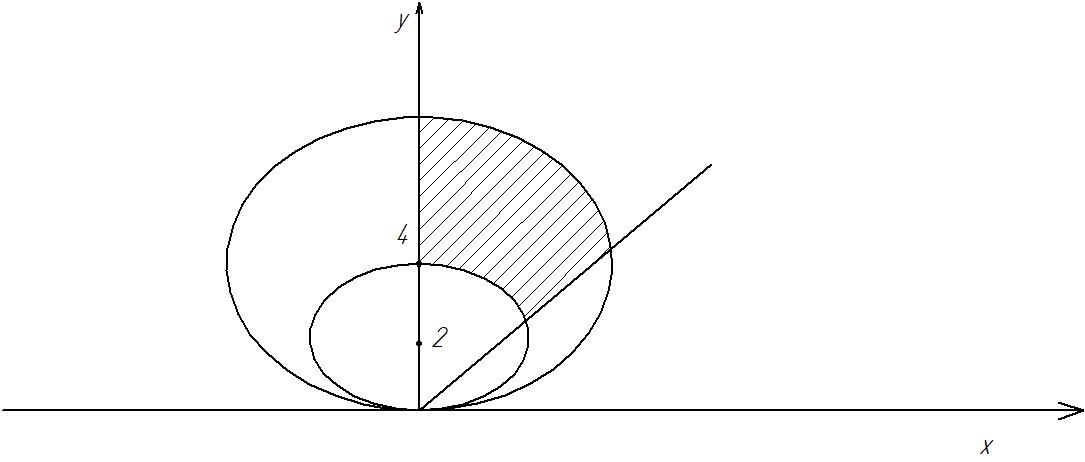
Рис. 3.10
Уравнения окружностей, в соответствии с вышеизложенным правило примут вид: ρ=4∙sinφ и ρ=8∙sinφ.
Пример:
вычислить
с помощью двойного интеграла в полярных
координатах площадь фигуры, ограниченной
кривой, заданной уравнением
Проведем замену переменных: x=ρcosφ, y= ρsinφ. Тогда заданная кривая в полярной системе координат примет вид:
где
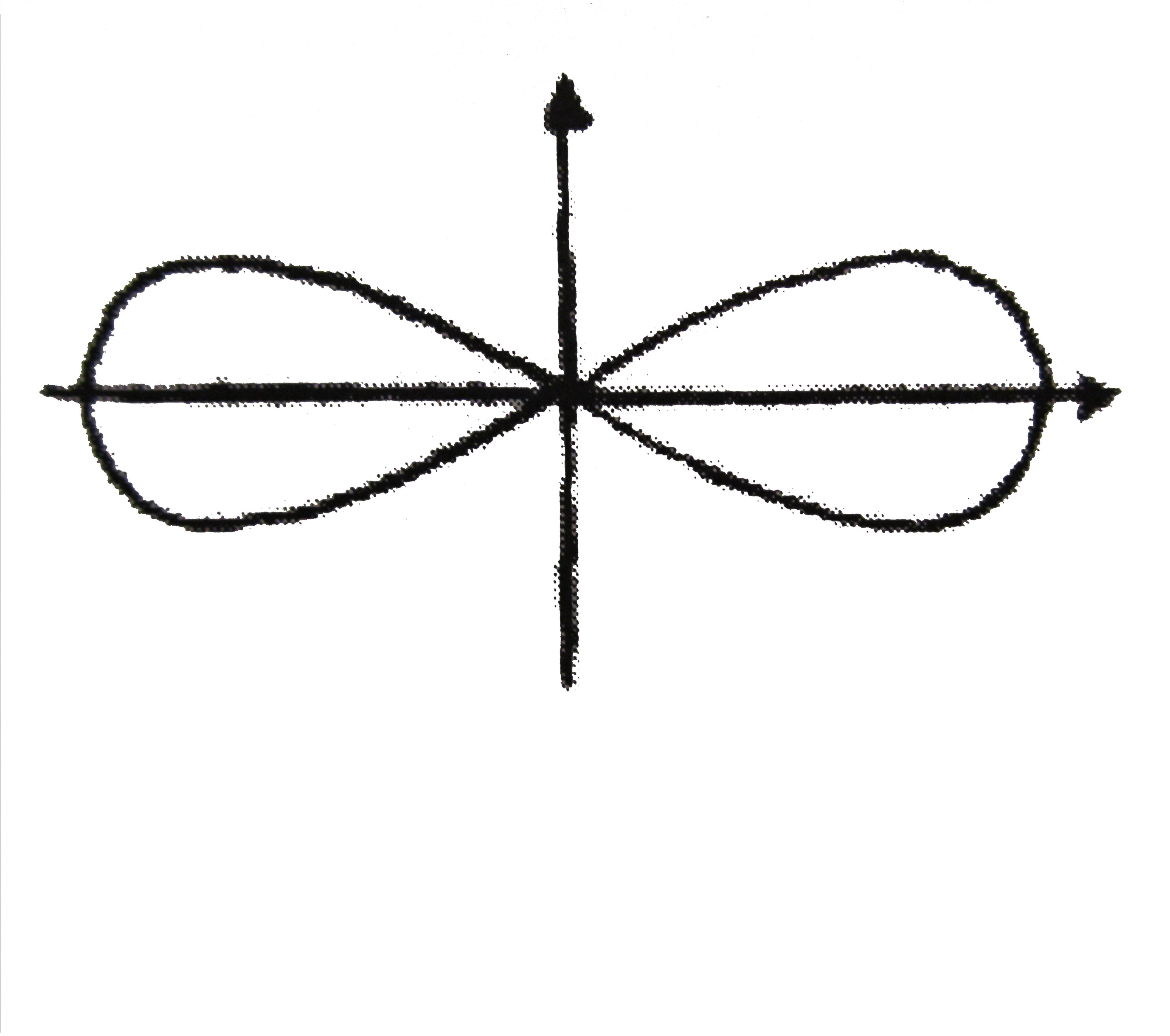
Рис.3.11
Тогда
С учетом того, что cos2
имеет период Т=π, и ρ≥0 параметр
С учетом симметрии фигуры (рис. 3.11), вычислим площадь четвертой части и результат умножим на четыре.
Вычислим
площадь по формуле
Площадь
всей фигуры, ограниченной данной линией,
S=2
.
Пример: найти массу пластинка G, если она задана ограничивающими её кривыми (рис. 3.12):
x
= 0, y
= 0,
,
-
поверхностная
плотность.
Рис. 3.12
Пластинка расположена в прямоугольной системе координат таким образом, что центры окружностей совпадают с началом координат.
.
Перейдем в двойном интеграле к полярным
координатам
при
этом область G
преобразуется в прямоугольную область
в полярной системе координат: 2≤ρ≤3,
-π/2 ≤φ≤0, поверхностная плотность:
Масса плоской пластины вычисляется по формуле:
Пример: найти статические моменты относительно координатных осей Ох и Oy однородной фигуры, ограниченной кривыми y²=ax, y=x (рис. 3.13) Т.к. фигура однородная, примем поверхностную плотность μ=const=1.
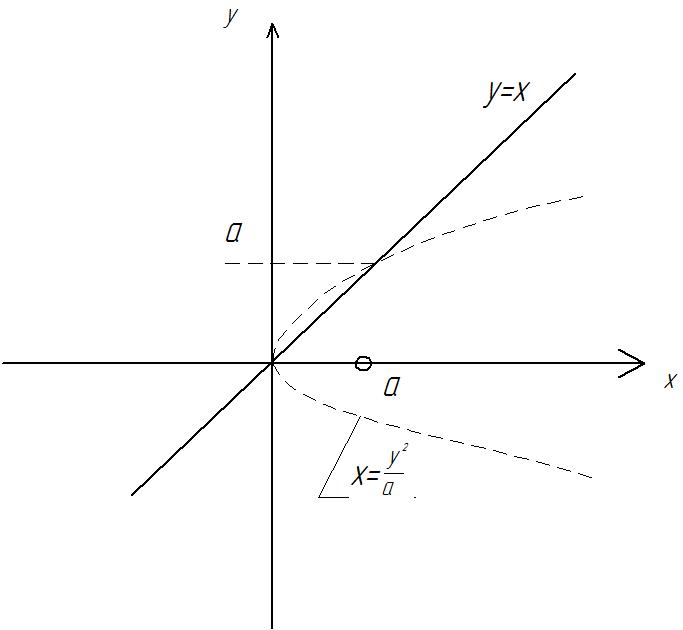
Рис.3.13
Статический момент относительно оси Ох
Статический момент относительно оси Оу
4.Тройные интегралы
Задача
о массе пространственного тела переменной
плотности f(x,y,z)
приводит к понятию тройного интеграла.
Под областью “V”,на
которую распространен тройной интеграл,
понимается ограниченная замкнутая
пространственная область, ограниченная
снизу и сверху поверхностями 
,
а с боков – цилиндрической поверхностью
с образующими, параллельными оси OZ.
Переменные x
и y
изменяются в плоской области 
,
которая является проекцией на плоскость
xoy
пространственной области “V”.
Функция f(x,y,z),
стоящая под интегралом должна быть
непрерывной и ограниченной в области
“V”.
Свойства тройного интеграла аналогичны свойствами двойного интеграла.