2.1 Дифференцирование сложных функций.
Пусть функция z=ƒ(x,y), дифференцируема в точке A(xo,yo), а функции x=X(t) и y=Y(t)- дифференцируемы по независимой переменной t, тогда z=ƒ[X(t),Y(t)] – сложная функция, в конечном счете, зависящая только от переменной t. Производная по аргументу t вычисляется по формуле:
dz/dt = ∂z/∂x ∙dx/dt + ∂z/∂y ∙dy/dt (2.1)
В формулу входят как полные, так и частные производные.
Пример: найти dz/dt, если z=x²+y²+x∙y, где x=sin t, y= tg t.
Найдем первые частные производные от функции z=ƒ(x,y): ∂z/∂x = 2x+y, ∂z/∂y=2y+x; найдем производные по попеременной t: dx/dt=cos t, dy/dt=1/(cos t)²=sec² t; тогда по формуле (2.1)
dz/dt = (2x+y)∙cos t + (2y+x)∙sec²t=(2sin t+tg t)∙cos t +(2tg t+sin t)∙sec²t
Пример: найти dz/dt, если z=arcsin(x-y), x=3t, y=4t³
Найдём
первые частные производные от функции
z=
ƒ (x,y):
= ; =
Найдём производные от функций x=X(t) и y=Y(t) по переменной t
Для окончательного решения примера воспользуемся формулой (2.1):
Если функция z= ƒ (x,y),а её аргументы сами являются функциями 2-х переменных, т.е.
x=X(u,v);
y=Y(u,v),
то тогда функция z=ƒ[X(u,v),
Y(u,v)]-
сложная функция переменных u
и v.
Тогда:
(2.2)
Пример:
найти и ,
если z=x2y-y2x,
где x=u
cos
v
, y=u
sin
v.
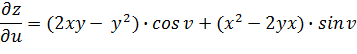
Пример:
найти
∂z/∂u
и ∂z/∂v,
если z=x²∙lny,
где
Найдем
частные производные и воспользуемся
формулой (2.2):
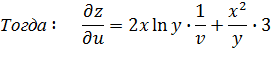
Если
функция
z=
ƒ(x,y),
а y=φ(x),
то z=
ƒ[x,φ(x)],
т.е. z
является сложной 
функцией
одного аргумента x,
поэтому будет существовать производная
dz/dx,
а т.к. z=f(x,y),
то
существуют частные производные
,
где (2.3)
Пример: найти и если z=xy²+x²y, а y=sinx
∂z/∂x = y²+2xy, ∂z/∂y=2xy+x², dy/dx = cosx
Тогда по формуле (2.3)
dz/dx
= (y²+2xy)+(2xy+x²)∙cosx
Пример: найти , если z=tg(3t+2x2); x=
2.2. Дифференцирование функций, заданных неявно.
Пусть
задано уравнение
F(x,y)=0,
причём
функция
F(x,y)
и
её частные производные
F´x(x,y)
и F´y(x,y)-определены
и непрерывны в некоторой окрестности
точки (x0,y0).
Пусть
F(x0,y0)=0,а
F´y(x,y)≠0.
Считаем,
что функция
y=ƒ(x)
неявно
задана уравнением F(x,y)=0.
Тогда существует производная (2.4)
Если
задано уравнение F(x,y,z)=0
и z=ƒ(x,y)-
функция, заданная неявно, то
(2.5)
Пример: найти если F(x,y)=xey+yex-exy=0
F´x=ey+yex-exy
y
; F´y=xey+ex-exy
x
Тогда в соответствии с формулой (2.4)
Пример: найти , если F(x,y,z)=z3+3xyz-a3
F´x=3yz ; F´y=3xz ; F´z=3z2+3xy
Тогда по формуле (2.5)
