1.2 Циклические коды

Широкое распространение получил класс линейных кодов, которые называются циклическими. Название этих кодов происходит от их основного свойства: если кодовая комбинация а₁, а₂, ...a_n-1, a_n принадлежит циклическому коду, то комбинации a_n, а₁ а₂, ..., a_n-1; а_n-1, a_n, a₁,..., a_n-2 и т. д., полученные циклической перестановкой элементов, также принадлежат этому коду.

Общим свойством всех разрешенных кодовых комбинаций циклических кодов (как полиномов) является их делимость без остатка на некоторый выбранный полином, называемый производящим. Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на этот полином.

Описание циклических кодов и их построение обычно проводят с помощью многочленов (полиномов). Цифры двоичного кода можно рассматривать как коэффициенты многочлена переменной x.

Поскольку любое число в произвольной системе счисления можно записать в виде

,

где x — основание системы счисления, a_n-1,…,a₀ — цифры этой системы, то переход от двоичного числа к записи в виде многочлена осуществляется следующим образом:

110111 ⁴ + 1 ³ + 0 ² + 1 + 1 ⁰ = ⁴ + ³ + + 1

Отсюда видно, что кодовая комбинация длиной n (n=5) описывается многочленом степени n - 1. Однако запись кодовой комбинации в виде многочлена не всегда определяет длину кодовой комбинации n. Например, при n = 5 многочлену x²+1 соответствует кодовая комбинация 00101. Поэтому при переходе к записи в виде кодовой комбинации необходимо дописывать нулевые старшие разряды.

Кодовые комбинации циклического кода описываются полиномами, обладающими определенными свойствами. Последние определяются свойствами и операциями той алгебраической системы, к которой принадлежит множество полиномов. В частности, в этой алгебраической системе, которая носит название поля Галуа (GF(x)), сложение над коэффициентами полиномов производится по модулю 2. Умножение полиномов должно производиться по модулю некоторого полинома P_r(x). Эти два условия определяют замкнутость указанных операций: их применение не приводит к кодовым комбинациям, длина которых больше длины заданного кода п.

Пусть n = 5. Сложим два полинома:

и .

Получим

Таким образом, степень полученного полинома P₃(x) не превышает n=5.

Умножение полиномов производится по модулю P_r(x). Это означает, что в качестве результата умножения принимается остаток от деления обычного произведения полиномов па полином P_r(x).

Напомним, что умножение чисел по модулю q сводится к тому, что обычное произведение этих чисел делится на q и записывается остаток. Например, 24 = 3 (mod 5), т. е. 24 = 8; 8:5 имеет в остатке 3. Это число и является результатом умножения по модулю 5.

Указанная операция над многочленами не приводит к появлению полинома с большей степенью, чем заданная длина кода.

Рассмотрим код с n=5. Возьмем P₁(x)=x⁴+x+1 и Р₂(x)=x⁴. Произведем обычное умножение полиномов:

.

Полином P₃(x), имея степень n=8, не принадлежит коду с n=5. Рассмотрим умножение по модулю P_r(x). При этом полином P_r(x) должен иметь степень r<n. Выберем P_r(x)=х³+х² +1. Находим P₁(x)P₂(x) [mod P_r(x)]=P₁(x)P₂(x):P_r(x), т. е.

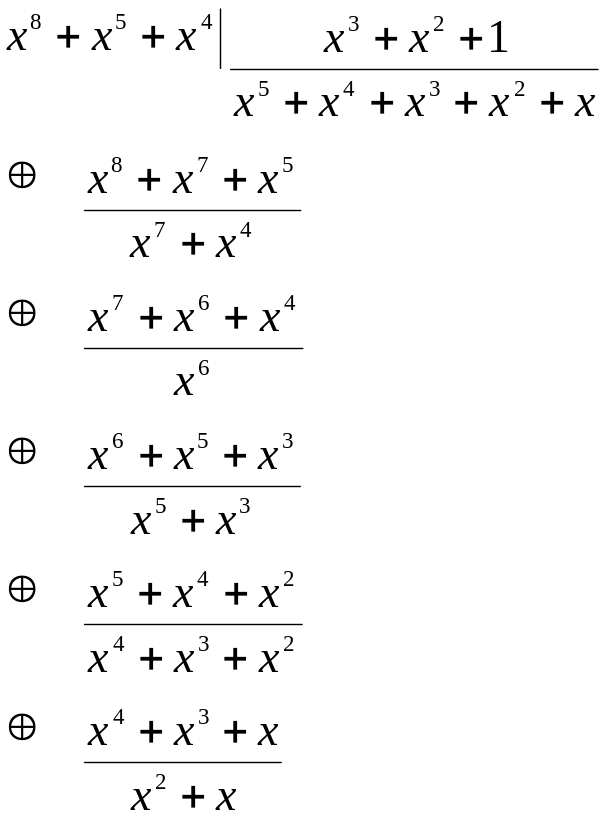
Таким образом, x²+x=R(x). Полученный остаток R(x)=х²+х и является результатом произведения полиномов P₁(x), P₂(x) по модулю P₃(x). Он именуется вычетом по многочлену P₃(x).

Для того чтобы полиномы, отображающие кодовые комбинации циклического кода, имели нужные свойства, необходимо выполнение двух условий: