1.1.5 Примеры линейных кодов

Рассмотрим простейший линейный код — код с одной проверкой на четность. Этот код независимо от длины кодовой комбинации содержит всего один проверочный элемент. Элемент выбирается таким, чтобы его сумма по модулю 2 со всеми информационными элементами равнялась нулю. При этом каждая кодовая комбинация содержит четное число единиц. Если в принятой кодовой комбинации окажется нечетное число единиц, то делается вывод о наличии в ней ошибок. Очевидно, что такой код обнаруживает любое нечетное число ошибок.

Производящая и проверочная матрицы такого кода имеют вид:

.

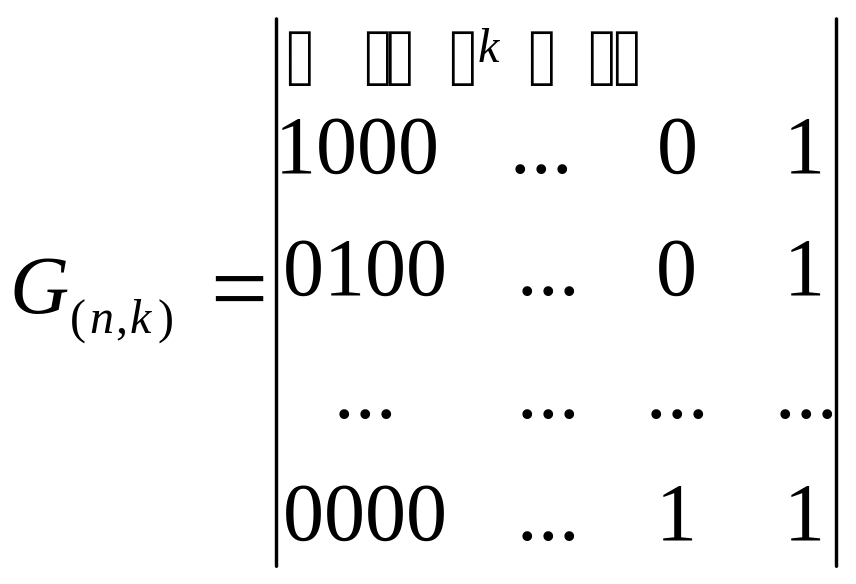
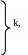
Для такого кода отношение числа информационных элементов k к длине кодовой комбинации n (скорость кода) определяется выражением

R_k = (n—l)/n,

кодовое расстояние равно двум, а вероятность необнаруженной ошибки

,

где суммирование осуществляется по всем четным значениям t.

Рассмотрим еще один пример линейных кодов — коды Хэмминга. К ним обычно относят коды с d₀=3, исправляющие все одиночные ошибки и коды с d₀=4, исправляющие все одиночные и обнаруживающие все двойные ошибки. Для исправления всех одиночных ошибок число синдромов должно быть n+1. Из них n синдромов используются для указания местоположения ошибки и один — нулевой, соответствует их отсутствию. Следовательно, 2^r  n+1, где r – число проверочных элементов. Последнее выражение можно переписать в виде

2^k2ⁿ/(n+1). (3.12)

В этом выражении k – число информационных элементов;

n – общее число элементов в кодовой комбинации.

Используя (3.12), можно подобрать при известном k требуемое число n.

Пример 3.7. Пусть k = 3. Требуется найти с помощью (3.12) значение n.

Задавая значения n=4, 5, 6, при n=5 получим 2ⁿ/(п+1) =5,3, т. е. 2³>5,3, а при n = 6 – 2/n+1=9,1. Так как 2³<9,1, то выбираем n = 6. Такой код может быть задан производящей матрицей или проверочной.

Рассмотрим далее код Хэмминга с d₀ = 4. Операция кодирования для такого кода может выполняться в два этапа. На первом этапе определяется кодовая комбинация с использованием матрицы Н, соответствующей коду с d₀=3, на втором добавляется один проверочный символ, представляющий собой результат суммирования по модулю 2 всех элементов кодового слова, полученного на первом этапе.

Операция декодирования также состоит из двух этапов. На первом — вычисляется синдром, соответствующий коду с d₀ = 3, на втором — проверяется последнее проверочное соотношение.

Пример 3.8. На основе кода (6,3), заданного проверочной матрицей (3.8), построить код Хэмминга с d₀ = 4.

Проверочная матрица такого кода будет иметь вид:

Такой код имеет дополнительное проверочное соотношение

и дополнительный элемент синдрома

.

Если синдром b₁b₂b₃ не равен нулю, а b₄ = 0, то это говорит о том, что произошла ошибка. Если b₁b₂b₃ не равен пулю и b₄  0, то это является признаком того, что была однократная ошибка. При равенстве нулю синдрома b₁b₂b₃ и b₄  0 имеет место ошибка нечетной кратности t3.

К линейным кодам относится также код с простым повторением, в основу которого положен метод повторения исходной кодовой комбинации. Декодирование осуществляется путем сравнения первой (информационной) и второй (проверочной) частей кода. При несовпадении этих частей комбинация бракуется. Скорость такого кода равна 1/2, а кодовое расстояние d₀=2. Проверочная матрица записывается в виде Н=|I_kI_k|, где I_k — единичная матрица. Такой код позволяет обнаружить все виды ошибок за исключением ошибок в «парных» элементах, т. е. элементах, стоящих на одних и тех же позициях в первой и второй комбинациях.

!