1. Помехоустойчивое кодирование

0. 1.1 Основные определения

1.1.1 Методы повышения верности передачи информации

Основной причиной ошибок являются помехи в непрерывном канале, а также его неидеальность (наличие линейных и нелинейных искажений). Причиной ошибок могут быть также неправильные действия персонала, осуществляющего как эксплуатацию различных участков канала связи, так и самой аппаратуры ПДС.

Условно разобьем методы повышения верности на три группы [5]. В первую группу включим меры эксплуатационного и профилактического характера, направленные на улучшение качественных показателей канала связи: повышение стабильности работы генераторного оборудования, резервирование электропитания систем передачи, выявление неисправного оборудования и его элементов и своевременная их замена, повышение культуры технического обслуживания и, в частности, принятие специальных мер предосторожности при проведении измерительных и профилактических работ на каналах во время передачи дискретных сообщений и т. п. Опыт показывает, что указанные мероприятия позволяют уменьшить вероятность ошибки на один бит в среднем в 5 раз.

Ко второй группе относятся мероприятия, направленные на увеличение помехоустойчивости передачи единичных элементов. Речь идет о таких мерах как повышение отношения сигнал-помеха за счет увеличения амплитуды, длительности или спектра частот полезного сигнала, применение более помехоустойчивых методов модуляции, более совершенных методов обработки сигналов па приеме и т. п. Применение большинства из перечисленных методов наталкивается на серьезные трудности. Так, сколько-нибудь существенно увеличить амплитуду сигналов, передаваемых по физической линии нельзя из-за опасности возникновения недопустимых переходов на соседние цепи. Если передача дискретных сообщений осуществляется по каналу ТЧ, то мощность дискретных сигналов ограничивается из-за необходимости не допустить перегрузку групповых усилителей. Увеличение длительности единичных элементов с одновременным введением интегрирования на приеме позволяет понизить вероятность ошибки на элемент; однако получить удовлетворительную верность при работе по каналам все же не представляется возможным, не говоря уже о неизбежном при этом снижении скорости передачи. Заметного эффекта можно достичь за счет использования сложных сигналов.

К третьей группе мер по повышению верности передачи дискретных сообщений относятся меры, связанные с введением избыточности в передаваемую по дискретному каналу последовательность. Следует заметить, что, используя эти методы, можно добиться существенного повышения верности.

При выборе способа введения избыточности следует исходить из того, что заданную верность передачи необходимо получить при минимальной избыточности. Должны приниматься во внимание и вопросы, связанные со сложностью реализации способа.

Перейдем к общим вопросам обнаружения и исправления ошибок в принимаемой последовательности элементов заданной длины.

1.1.2 Понятие о корректирующих кодах

Код, способный обнаруживать или исправлять ошибки, называется корректирующим.

Каждому символу исходного алфавита А сообщений объема N_А (число символов в алфавите) поставим в соответствие n-элементную двоичную последовательность (кодовую комбинацию). Возможное (общее) число последовательностей длины n равно N₀ = 2ⁿ. Для обнаружения (и - или исправления) на приеме ошибок должно соблюдаться условие N_А < N₀ , где N₀ – объём сообщений кодера.

Если N_A=N₀, то все возможные последовательности n-элементного кода используются для передачи, или, как говорят, являются разрешенными. Полученный таким образом код называется простым, т. е. неспособным обнаруживать (исправлять) ошибки.

Пример 3.1. Для передачи сообщений, число которых равно 8 (N_A = 8), используется трехэлементный код. Число комбинаций, которое можно при этом получить, N₀ = 2³=8. Комбинации, образуемые трехэлементным кодом, представлены в табл. 3.1.

Таблица 3.1  Комбинации, образуемые равномерным трёхэлементным кодом

Номер комбинации	0	1	2	3	4	5	6	7
Вид комбинации	000	001	010	011	100	101	110	111

Отсюда видно, что комбинация № 0 отличается от комбинации № 1 только в одной позиции. Следовательно, если при передаче комбинации 000 произойдет ошибка в третьем элементе, то получим комбинацию 001 — комбинацию № 1, т. е. произойдет ошибка, которую невозможно ни исправить, ни обнаружить.

Степень различия комбинаций характеризуется расстоянием Хемминга. Расстояние Хэмминга для любых двух кодовых комбинаций определяется числом несовпадающих в них разрядов. Например, две написанные ниже друг под другом комбинации не совпадают в двух разрядах.

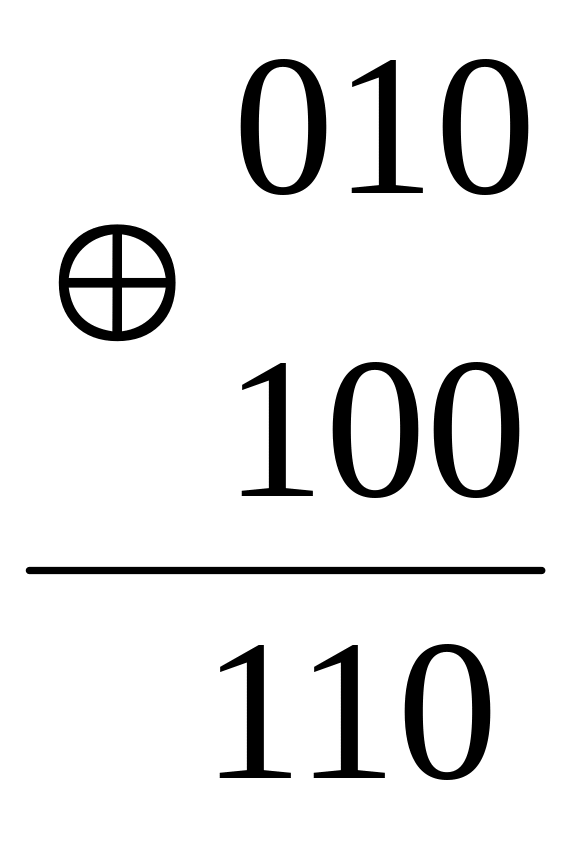
Поэтому хэммингово расстояние d=2.

Иначе, расстояние Хемминга определяют как вес суммы по модулю 2 ( — условное обозначение суммы по модулю 2) этих кодовых комбинаций. Весом W кодовой комбинации называется число входящих в нее ненулевых элементов.

Перебрав все возможные пары кодовых комбинаций, можно найти минимальное значение d, которое будем обозначать в дальнейшем d₀ и называть кодовым расстоянием. Для примера 3.1 d₀= 1. Рассмотренный в примере код является простым. Любая ошибка (даже одиночная!) при использовании такого кода приведет к тому, что переданная разрешенная кодовая комбинация перейдет в другую разрешенную кодовую комбинацию. Таким образом, простой код не способен обнаруживать и тем более исправлять ошибки и имеет d₀= 1.

Для того чтобы код мог обнаружить ошибки, необходимо соблюдение неравенства N_A<N₀. При этом неиспользуемые n-элементные кодовые комбинации, число которых (N₀ - N_A), будем называть запрещёнными. Они определяют избыточность кода. Очевидно, что появление ошибки в кодовой комбинации будет обнаружено, если переданная разрешенная комбинация перейдет в одну из запрещенных. В качестве разрешенных кодовых комбинаций надо выбирать такие, которые максимально отличаются друг от друга.

Пример 3.2. Алфавит передаваемых сообщений N_A = 2. Выберем из числа комбинаций, представленных в табл. 3.1, две. Очевидно, что ими должны быть комбинации 000, 111 или 001 и 110 и т. д. Кодовое расстояние do=3. Ошибки кратности один или два превращают любую кодовую комбинацию в запрещенную. Следовательно, максимальная кратность обнаруживаемых таким кодом ошибок равна двум (t_о.ош =2).

Рассматривая коды с кодовым расстоянием d₀= 4, d₀= 5 и т. д., можно прийти к выводу, что

t_о.ош = d₀ — 1.

Исправление ошибок возможно также только в том случае, если переданная разрешенная кодовая комбинация переходит в запрещенную. Вывод о том, какая кодовая комбинация передавалась, делается на основании сравнения принятой запрещенной комбинации со всеми разрешенными. Принятая комбинация отождествляется с той из разрешенных, на которую она больше всего «похожа», т. е. с той, от которой она отличается меньшим числом элементов. Так, если в примере 3.2 при передаче кодовой комбинации 000 получим 001, то вынесем решение, что передавалась комбинация 000.

Связь между d₀ и кратностью исправляемых ошибок определяется выражением

t_и.ош = d₀ /2—1

для четного d₀ и

t_и.ош = (d₀ – 1)/2

для нечетного d₀.

Итак, задача получения кода с заданной корректирующей способностью может быть сведена к задаче выбора (путем перебора) из N₀ = 2ⁿ кодовых комбинаций, комбинаций с требуемым минимальным кодовым расстоянием d₀. Если n достаточно мало, то такой перебор не представляет особого труда. Но при больших n перебор может занимать значительное время. Поэтому па практике получили распространение методы построения кодов, не требующие перебора с целью получения кода с заданным d₀ и отличающиеся приемлемой сложностью реализации.

Помехоустойчивые (корректирующие) коды делятся на блочные и непрерывные. К блочным относятся коды, в которых каждому символу алфавита сообщений соответствует блок (кодовая комбинация) из n_i элементов, где i — номер сообщения. Если n_i = n, т. е. длина блока постоянна и не зависит от номера сообщения, то код называется равномерным. Такие коды нашли наибольшее применение на практике. Если длина блока зависит от номера сообщения, то блочный код называется неравномерным. В непрерывных кодах передаваемая информационная последовательность не разделяется на блоки, а проверочные элементы размещаются в определенном порядке между информационными (проверочные элементы в отличие от информационных, относящихся к исходной последовательности, служат для обнаружения и исправления ошибок и формируются по определенным правилам).

Равномерные блочные коды делятся на разделимые и неразделимые. В разделимых кодах элементы разделяются на информационные и проверочные, занимающие определенные места в кодовой комбинации. В неразделимых кодах отсутствует деление элементов кодовых комбинаций на информационные и проверочные. К таким кодам относятся коды с постоянным весом, например, рекомендованный Международным Союзом по Электросвязи (МСЭ) семиэлементный телеграфный код № 3.

Полезный эффект от применения корректирующих кодов заключается в повы-шении верности передачи информации. Вероятность неправильного приема кодовой комбинации простого кода (индексы: внизу означают неправильного приёма; вверху – простого кода) определяется как вероятность появления в кодовой комбинации хотя бы одной ошибки Р_n(t 1).

В случае независимых ошибок

= 1 — (1—р_ош)^k,

где р_ош — вероятность неправильного приема единичного элемента,

k — число элементов в комбинации простого кода (число информационных элементов).

При использовании систематических корректирующих кодов к исходной комбинации добавляются проверочные элементы, позволяющие исправлять или обнаруживать ошибки. Так, если код используется в режиме исправления ошибок (индекс вверху - И) и кратность исправляемых ошибок t_и.ош, то

.

В результате применения корректирующего кода в режиме исправления ошибок вероятность ошибочного декодирования уменьшается в k_и раз:

.

Однако это достигается за счет увеличения затрат на реализацию системы и снижения скорости передачи информации. Если в системе, использующей простой код, скорость равна бит/с, то в системе, использующей корректирующий код с исправлением ошибок, скорость

,

где k/n — коэффициент, характеризующий потери скорости вследствие введенной в код избыточности и называемый иногда скоростью кода.

Чем больше избыточность (меньше k/n), тем меньше скорость передачи информации, т. е. тем меньше в единицу времени передается полезной информации.

Кодирование будет экономически оправданно, если стоимость S₁ устранения ошибки в единичном элементе (бите) с помощью исправления ошибок меньше стоимости потерь (S₂), вызнанных искажением единичного элемента при передаче. Величина S₂ может колебаться в очень больших пределах. Стоимость устранения ошибки в единичном элементе определяется выражением

(3.1)

где S_И — стоимость системы исправления ошибок;

S_ДОП — дополнительные затраты на аренду канала, обусловленные передачей по каналу проверочных элементов;

Т — время жизни системы исправления ошибок;

R_И — скорость передачи информации, бит/с;

— вероятность ошибки на элемент;

— коэффициент, характеризующий уменьшение вероятности шибки на элемент за счет исправления ошибок ( ).

Очевидно, что в (3.1) определяет число ошибочных элементов, выданных получателю за время жизни системы, а — эквивалентную вероятность ошибки после исправления. Экономическая эффективность за счет исправления ошибок S = S₂—S₁. Исправление ошибок имеет смысл при S 0.

Качество реальных каналов во времени меняется, и если заданы требования на верность передачи, то требуется вводить такую избыточность, которая обеспечивала бы заданную верность даже при самом плохом качестве канала. Напрашивается мысль о целесообразности изменения избыточности, вводимой в кодовую комбинацию по мере изменения характеристик канала связи.

Системы, в которых меняется избыточность с изменением качества канала, относятся к числу адаптивных.

Одним из типов адаптивных систем являются системы с обратной связью. В этих системах между приемником и передатчиком помимо основного (прямого) канала имеется вспомогательный (обратный) канал.

Следует заметить, что системы без обратной связи используются обычно тогда, когда нельзя организовать обратный канал или когда предъявляются весьма жесткие требования ко времени задержки сообщения. Временем задержки кодовой комбинации называется время от момента выдачи ее первого элемента источником сообщений до момента получения последнего элемента комбинации получателем сообщений.