ФИНАНСОВЫЕ И КОММЕРЧЕСКИЕ РАСЧЕТЫ

Тема 1. В финансовом анализе есть всего две операции: наращивание и дисконтирование.

1. Начисление процентов

Проценты (Int) – абсолютная величина дохода о предоставления денег в долг.

Процентная ставка (i) – относительная величина дохода от предоставления денег в долг.

Период, к которому относится процентная ставка называется периодом начисления.

Сумма, которая образуется в результате сложения первоначальной суммы долга с процентами, называется наращенной суммой: S=P+Int.

Наращение – приведение сегодняшних денег к будущему моменту времени.

Проценты бывают простые и сложные. Простые проценты – база начисления процентов не меняется (P= const). Сложные проценты - база начисления меняется. Два метода: декурсивный – проценты начисляются на первоначальную сумму долга (P); антисипативный – проценты начисляются как скидка с конечной суммы задолженности (S).

2. Простые проценты

А) декурсивный метод (P).

Int = Pin

P+Int= P+pin

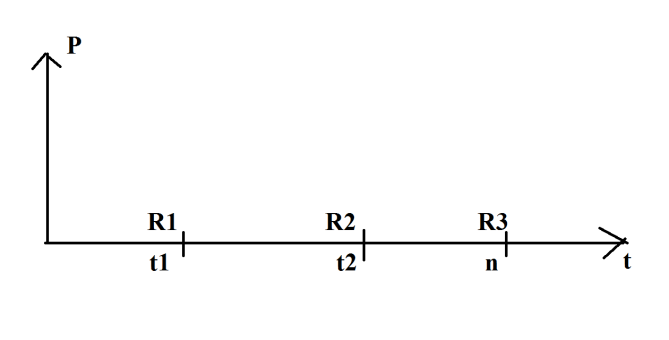
S = P(1 + ni)

1. i=const.

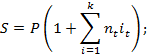
2. Реинвестирование (рефинансирование):

3. t-количество дней, которое может или фактическим, или определенным (30 дней), k – количество годовых дней: (360), (365), (365, 366). Базисы для расчета:

0 – 30/360 (ам. метод).

1 – факт/365, 366

2 – факт/360

3 – факт/365

4 – 30/360 (ев. метод).

По умолчанию: берем 4 базис, если в задаче нет другого условия. 1 базис, если речь идет о доходности, эффективности операции.

Пример 1. Погашение краткосрочных займов

1. Актуарный метод: проценты начисляются на остаток задолженности.

где .

1. 

2. 

3. 

Замечание: если первый платеж (R1) оказывается меньше, чем проценты, начисленные за данный период, то, как платеж он не считается, а его сумма добавляется к следующему платежу.

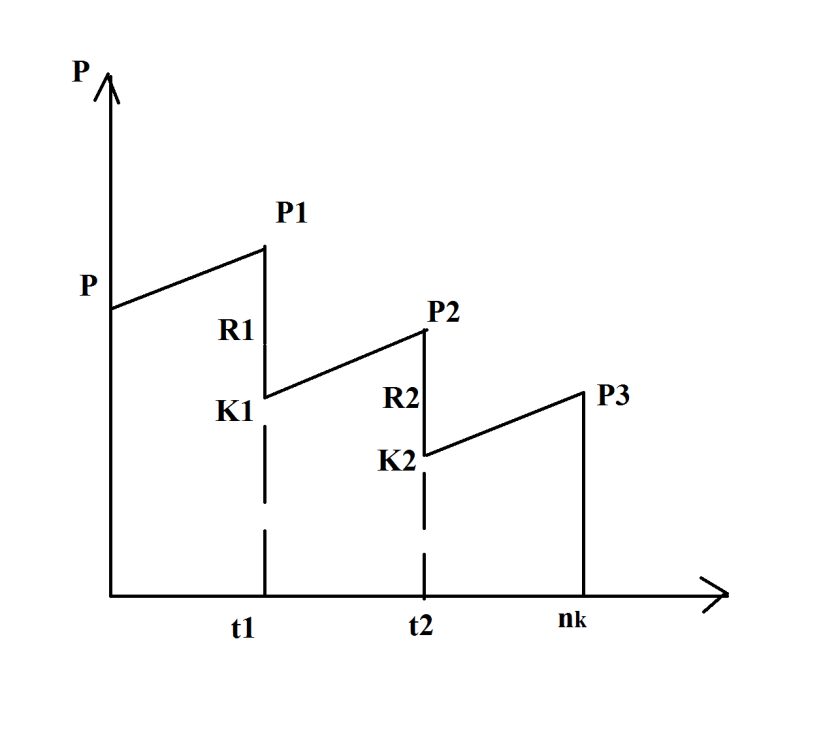
2. Метод торговца.

В методе торговца сумма долга и все выплаты приводятся на конец периода, последний платеж получается как разница между приведенным долгом и суммой приведенных платежей.

Замечание: иногда, если срок более года, то сначала наращивается и вычитается все на конец первого года, в результате определяется остаток долга, относительно которого происходит наращение и вычитание в следующем году.

Выгоднее тот метод, в котором последний платеж оказывается меньше.

Пример 2. Конверсия валюты и приращение процента

Ситуации:

1. Рубли – рубли (i);

2. Рубли - конверсия в валюту – валюта – конверсия в рубли (j);

3. Валюта – конверсия в рубли – рубли – конверсия в валюту.

К1 – минимальное;

K₁>K₁^min – операции с конверсиями выгоднее.

К1 – критическое.

K₁<K^кр – операция с конверсия убыточна (неэффективна).

Б) Антисипативный метод.

1. Математическое дисконтирование. Дисконтирование - приведение будущих денег к сегодняшнему моменту времени.

МН:

ДМ:

2. Учёт векселей. d – учетная ставка векселей. D – дисконт

МН:

ДМ:

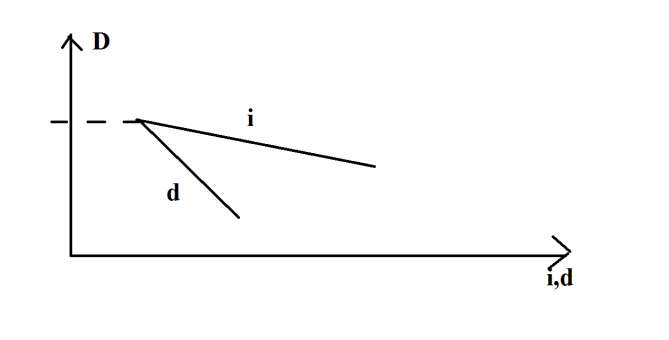
Используем учет векселей только в случае, если в задаче есть слово «вексель» или учетная ставка.

2. Сложные проценты.

А) Декурсивный метод.

Замечания:

1. Сложные проценты используем, сели срок более года, простые, – если срок менее года.

МН:

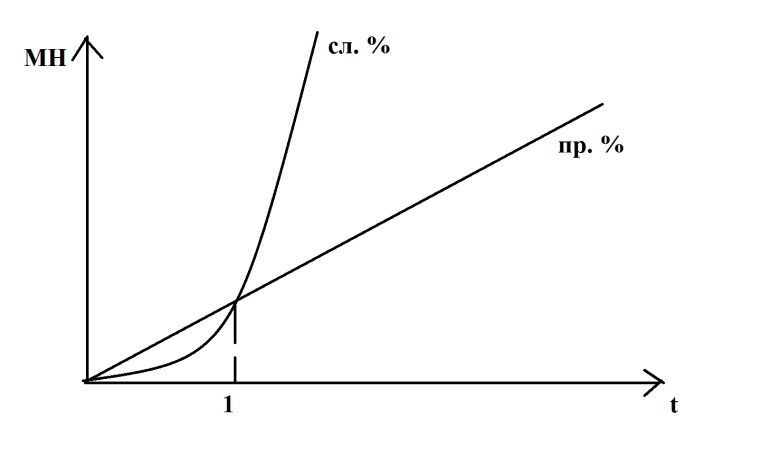
2. Очень часто предлагается начисление процентов несколько раз в год (m). m = 1,2,4,12.

`

3. Если дробное количество лет.

4. Переменная ставка:

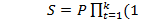
Б) Антисипативный метод

1. Математическое дисконтирование.

2. Учетные операции (Не применяются на практике).

3. Если проценты начисляются m раз в год, то – единичный МН.

Пример 1.

Операция по вкладам.
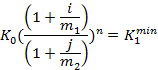
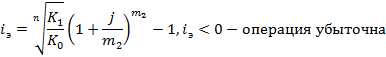