
- •Рациональные алгебраические выражения Глава VIII. Алгебраические дроби Знакомимся с алгебраическими дробями
- •I ступень
- •II ступень
- •369. Заполните таблицу
- •III ступень
- •I ступень
- •II ступень
- •III ступень
- •Проверьте себя
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •Глава IX. Операции с алгебраическими дробями Складываем и вычитаем алгебраические дроби
- •417. Выполните действия:
- •I ступень
- •422. Выполните действия:
- •424. Выполните действия:
- •II ступень
- •III ступень
- •Умножение и деление алгебраических дробей
- •473. Выполните действия:
- •I ступень
- •II ступень
- •III ступень
- •Проверьте себя
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •Глава х. Степени с целым показателем Выполняем все действия со степенями
- •I ступень
- •II ступень
- •III ступень
- •Проверьте себя
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •III ступень
- •1 Вариант
- •1. Выполните действия:
- •2 Вариант
- •3 Вариант
I ступень
386. 1) Ученик сократил дробь так:
а)
![]() б)
б)
![]()
Можете ли вы предложить другой способ сокращения дробей?
2) Сократите дробь:
а)
![]() б)
б)
![]() в)
в) ![]() г)
г)
![]() д)
д)
![]() е)
е)
![]()
387.
Среди данных дробей найдите все дроби,
тождественно равные дроби
![]()
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]()
388. Объясните, как выполнено сокращение дроби.
Решение 1.
![]()
Решение 2.
![]()
Придумайте два аналогичных примера.
389. Найдите числовые значения дроби:
а)
![]() при x
= 2,5 и x
=
при x
= 2,5 и x
=
![]() б)
б)
![]() при x
=
и x
= –1,8.
при x
=
и x
= –1,8.
390. Сократите дробь, если это возможно:
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
![]() е)
е)
![]()
ж)
![]() з)
з)
![]() и)
и)
![]()
к)
![]() л)
л)
![]() м)
м)
![]()
н)
![]() о)
о)
![]() п)
п)
![]()
р)
![]() с)
с)
![]() т)
т)
![]()
391. Придумайте примеры дробей:
1) числитель и знаменатель которых сокращаются:
а) на число; б) на одночлен; в) на многочлен;
2) для сокращения которых применялись бы:
а) тождества сокращенного умножения;
б) разложение на множители методом группировки.
392. Найдите дополнительный множитель:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
393. Запишите числитель дроби:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
394. Приведите дроби к общему знаменателю как можно более простого вида:
а)
![]() и
и
![]() б) d
и
б) d
и
![]()
в)
![]() и
и
![]() г)
г)
![]() и
и
![]()
д)
![]() е)
е)
![]()
ж)
![]() и
и
![]() з)
з)
![]() и
и
![]()
и)
![]() к)
к)
![]() и
и
![]()
л)
![]() и
и
![]() м)
м)
![]() и
и
![]()
н)
![]() о)
о)
![]() и
и
![]()
395. Найдите числовое значение выражения:
а)
![]() б)
б)
![]() в)
в)
![]()
396. Известно, что площадь круга вычисляется по формуле S = r2, где r – радиус круга; длина окружности вычисляется по формуле с = 2r. Найдите отношение длины окружности к площади круга.
II ступень
397. 1) Продолжите цепочку равенств:
а)
![]() б)
б)
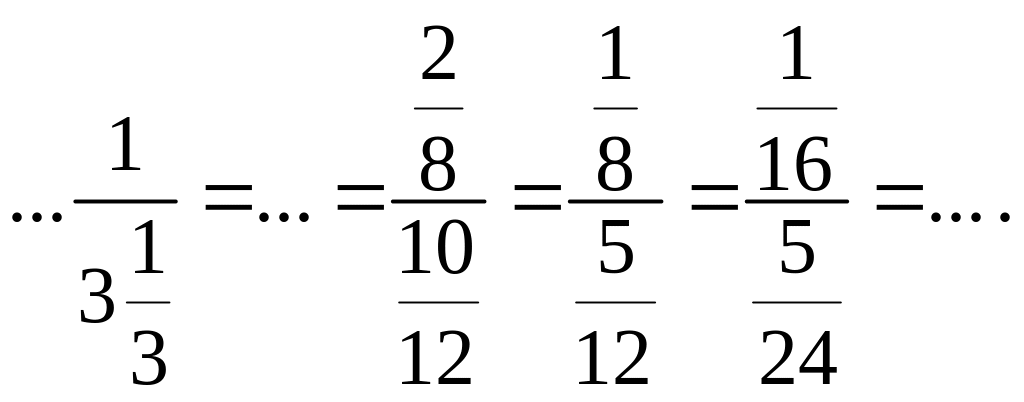
2) Может ли в первой цепочке оказаться дробь:
а)
![]() б)
б)
![]() в)
в)
![]()
3) Может ли оказаться во второй цепочке дробь:
а)
![]() б)
б)
![]()
4) Могли бы вы в данном задании при приведении числовых выражений к обыкновенной дроби использовать следующие приемы?
– Найти наименьшее общее кратное знаменателей обыкновенных дробей, из которых составлены данные алгебраические дроби; умножить числитель и знаменатель алгебраической дроби на полученное число.
– Уравнять число знаков после запятой у всех десятичных дробей, входящих в алгебраическую дробь; отбросить в них запятую.
Надо ли запоминать эти приемы, может быть, достаточно помнить основное свойство алгебраической дроби?
398. 1) Представьте дробь в виде обыкновенной дроби:
а)
![]() б)
б)
![]() в)
в)
![]()
2) Преобразуйте алгебраическое выражение в алгебраическую дробь:
а)
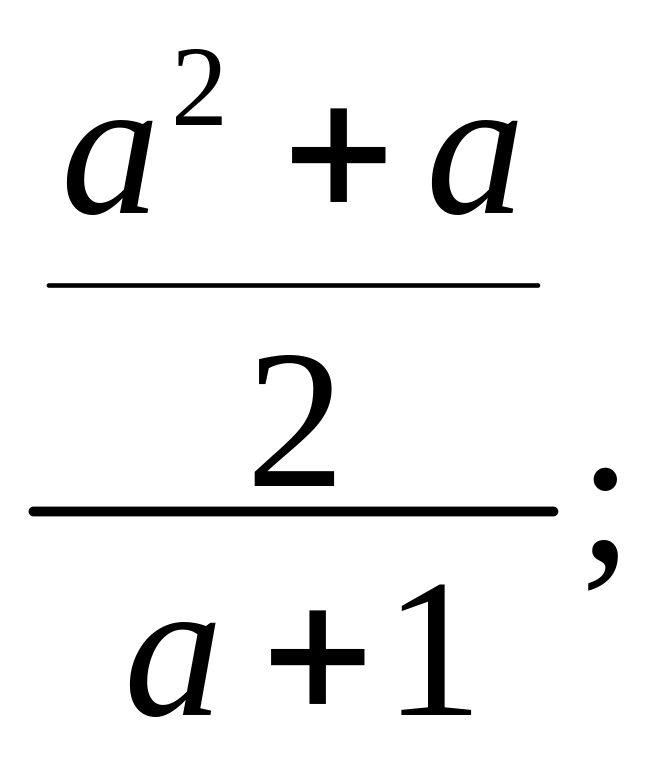 б)
б)
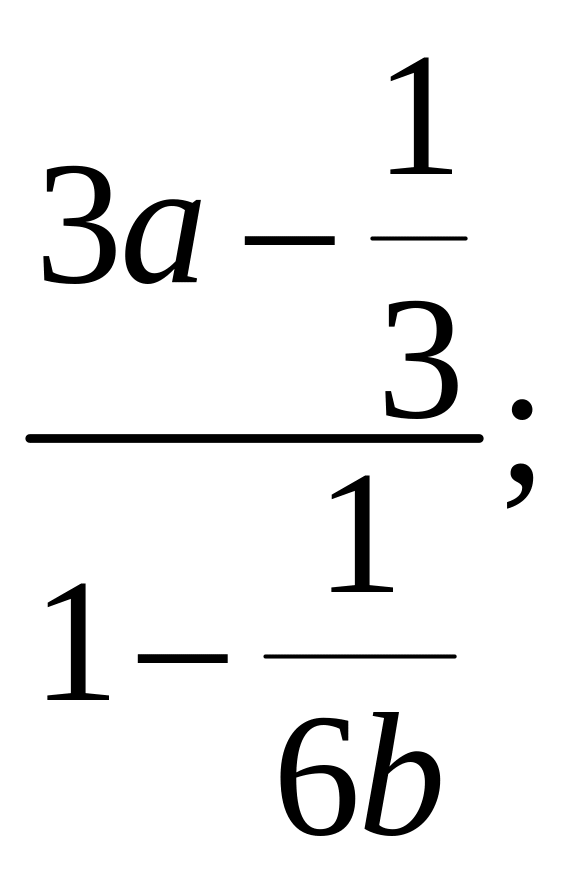 в)
в)
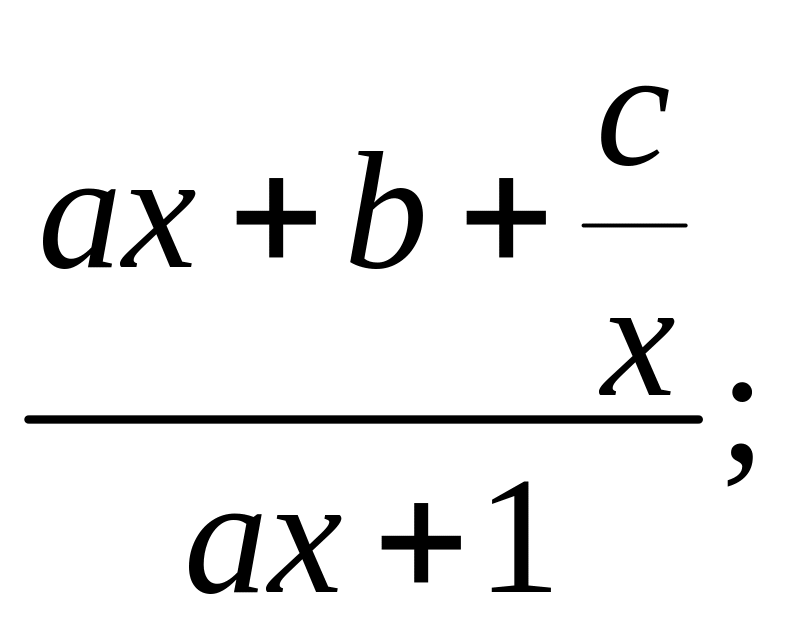 г)
г)
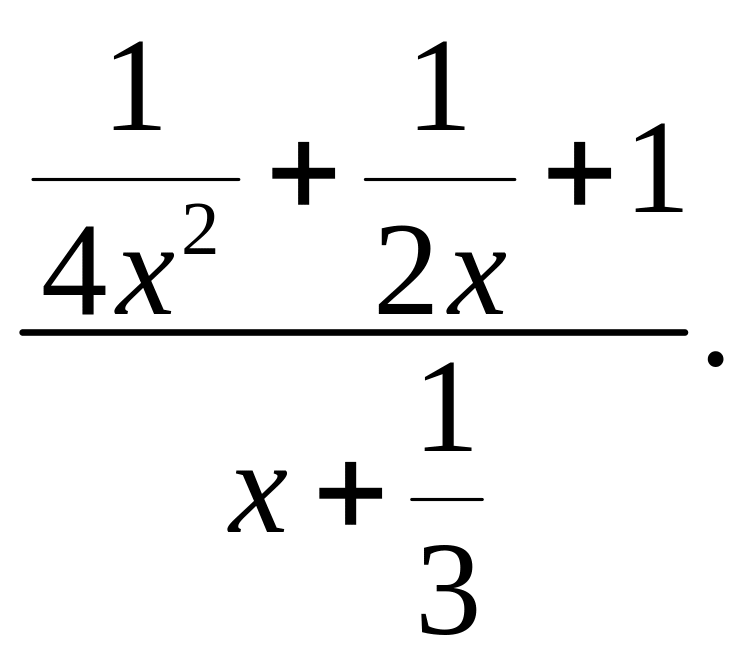
399. Найдите целое выражение наиболее простого вида, которое делится нацело на каждый из следующих многочленов:
а) х + 1, х – 1; б) (х – 1)2, х2 – 1; в) т2 – 2тп + п2, т2 + п2;
г) а – b, а + b, b2 – а2; д) х2 – 2х + 1, 1 – х; е) а + b, b – а, а2 – b2;
ж) 4а2 – 12а + 9, 8а – 12, 2а2 – 3а.
400. 1) Установите, равны ли дроби:
а)
![]() и
и
![]() б)
б)
![]() и
и
![]() в)
в)
![]() и
и
![]()
2) Для каждой дроби запишите еще по две, равные ей.
401. 1) Примите участие в конкурсе на лучшего «вычислителя». Победит тот, кто быстрее и без ошибок сократит дробь:
a)
![]() б)
б)
![]() в)
в)
г)
![]() д)
д)
![]() е)
е)
![]()
ж)
![]() з)
з)
![]() и)
и)
![]()
к)
![]() л)
л)
![]() м)
м)
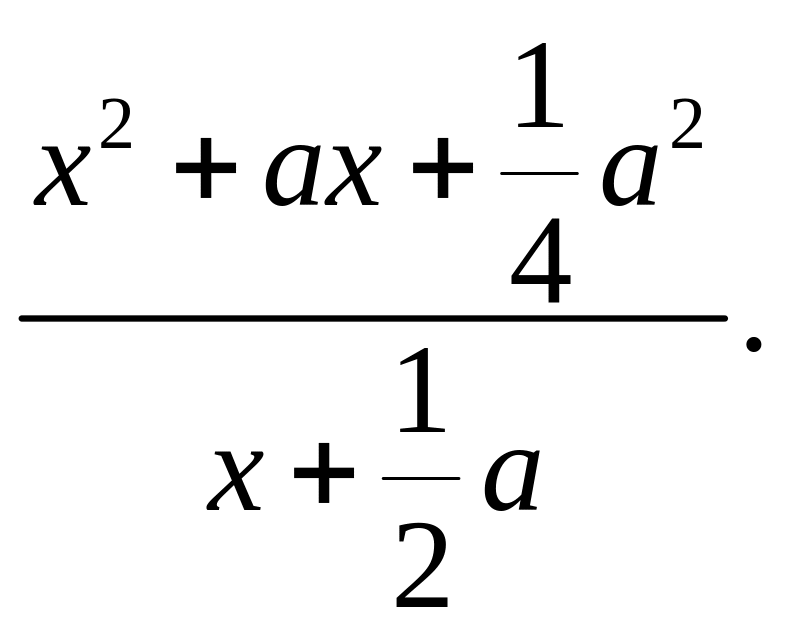
2) Придумайте свои задания для такого конкурса.
402. Заполните пропуски, чтобы полученную дробь можно было сократить:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]()
403. Известно, что т – п = 9. Найдите значение дроби:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
404. Найдите значение алгебраической дроби:
а)
![]() если
если
![]()
б)
![]() если
если
![]()
405. Приведите дроби к общему знаменателю:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]()
406. Придумайте два интересных примера на основное свойство алгебраических дробей.
