5.1.2.1.3. Спостереження інтерференції світла

Забезпечити сталість різниці фаз коливань, необхідну для спостереження інтерференції світла, можна двома принципово різними способами. Один з них полягає в тому, щоб узгодити фази випромінювань окремих атомів. Це досягається, наприклад у лазерах. Інший спосіб зводиться до того, щоб змусити інтерферувати хвилі, які приходять у точку спостереження від того ж самого атома, але різними шляхами. Найпростіший приклад - схема, що складається з джерела світла і дзеркала (рис. 5.1.11).У кожну точку простору, наприклад В, коливання від кожного атома джерела S приходять двома шляхами: по прямому променю SB = r₁ і по променю SAB = r₂, відбитому від дзеркала. Оскільки r₂ > r₁, то коливання, що йде шляхом SAB, буде запізнюватися відносно того ж коливання, що йде шляхом SB, на час Dt = |r₁ - r₂| / , де - швидкість світла. Різницю відстаней r₁ - r₂ = Dr, які проходять коливання від джерела до місця зустрічі, називають різницею ходу променів.

У точках простору, для яких різниця ходу променів менша довжини цугу,

|r₁ - r₂| < L_цуга , (5.1.11)

(див., наприклад, точку В на рис. 5.1.11), цуг, що приходить сюди довшим шляхом r₂, ще застане той же цуг, що йде коротшим шляхом r₁ - тут цуг "інтерферує сам із собою''. При цьому різниця фаз Dj коливань, оскільки вони відходять від джерела одночасно, визначається тільки часом запізнення. Вона є однаковою для всіх наступних цугів, що один за одним випускаються атомом, і тому постійною у часі. Тому всюди, де виконується умова (5.1.11), коливання є когерентними і має місце їх інтерференція.

Оскільки на відстані, рівній довжині хвилі l, фаза хвилі змінюється на 2p, то різниці ходу Dr = r₁ - r₂ відповідає різниця фаз

. (5.1.12)

Підставляючи у вираз (5.1.12.) , одержуємо умову максимумів:

Dr = kl = 2k , k = 0, ± 1, ± 2, … . (5.1.13)

Таким чином, взаємне підсилення хвиль (див. формулу (5.1.6) і рис. 5.1.9, а) має місце в тих точках простору, для яких різниця ходу дорівнює цілому числу довжин хвиль (парному числу півхвиль).

Аналогічно, підставляючи у (5.1.12.) Dj =(2k + 1)p, одержуємо умову мінімумів:

Dr = (2k +1) , k = 0, ± 1, ± 2 . (5.1.14)

Згідно з (5.1.14) взаємне ослаблення хвиль (див. формулу (5.1.9) і рис. 5.1.9, б) має місце в тих точках простору, для яких різниця ходу дорівнює непарному числу півхвиль.

У точках простору, для яких |Dr| > L_цуга (наприклад, у точці В₁ на рис. 5.1.11), цуг, що приходить сюди довгим шляхом, вже не зустрінеться з тим же цугом, що йшов коротким шляхом (як видно з рисунка, останній вже пройде точку спостереження). Він зустрічається з одним з наступних цугів, випущених атомом. При цьому різниця фаз коливань, що складаються, у міру приходу нових цугів хаотично змінюється (цуги випускаються безладно у часі). Таким чином, в області, де співвідношення (5.1.11) не виконується, коливання не є когерентними й інтерференція відсутня. У зв'язку з цим співвідношення (5.1.11) називають умовою когерентності. Там, де виконується умова когерентності, спостерігається інтерференційна картина - характерний нерівномірний розподіл інтенсивності світла.

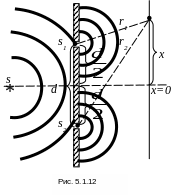О дним з перших дослідів з інтерференції світла був дослід Юнга. Від джерела світла S розповсюджується сферична хвиля, на шляху якої розміщена перешкода. В ній зроблено два отвори S₁ та S₂, симетричних відносно осі симетрії (вісь перпендикулярна до перешкоди). Отвори будуть двома джерелами когерентних хвиль, бо вони отримані від одного хвильового фронту. На екрані в різних точках (зверху та знизу) буде проходити накладання двох хвиль (рис. 5.1.12). Очевидно, що в точці х=0 буде спостерігатись центральний максимум, бо сюди хвилі завжди приходять з різницею фаз, рівною нулю (тобто в фазі). Залежно від положення точки на екрані будуть спостерігатись плавний перехід від максимумів освітленості (інтенсивності світла) до мінімумів (темні смуги). В розділі 5.3 „Приклади розв’язування задач по модулю 5” детально розглянуто приклад розрахунку інтерференційної картини для такого випадку, а також інші приклади інтерференції, що допоможуть глибше вникнути в деталі цього важливого явища. Важливо зазначити, що в різних прикладах інтерференційна картина може мати вигляд системи концентричних кілець: світлі і темні кільця чергуються одне з одним (так звані кільця Ньютона); може складатися із світлих і темних паралельних смуг тощо.