5.1.1.5. Формула лінзи. Оптична сила лінзи
З геометричних міркувань та побудови зображень в лінзі випливає співвідношення між відстанями від лінзи до зображення та до предмета та фокусною відстанню лінзи:
,
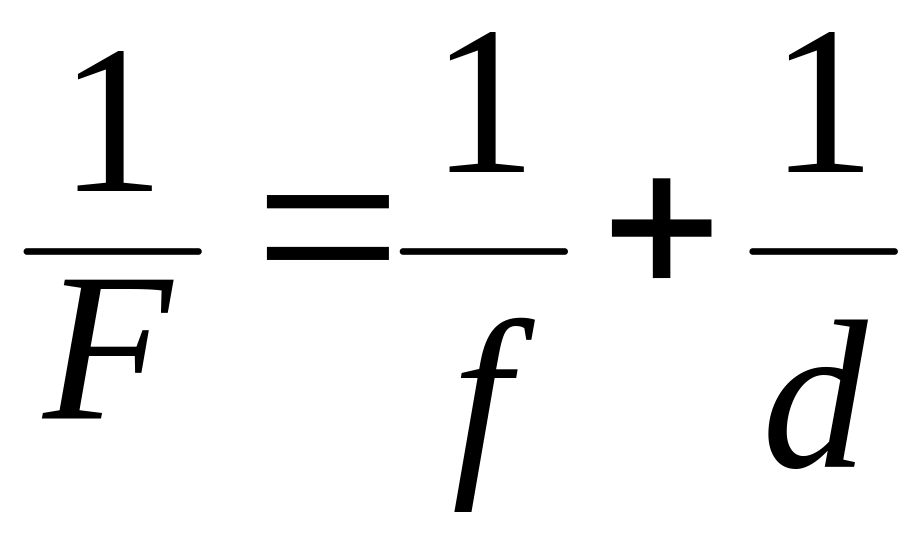(5.1.3.)
де f та d - відстань від лінзи до зображення та до предмета, відповідно; F – фокусна відстань лінзи.
Лінза з більш опуклими поверхнями заломлює промені сильніше, ніж лінза з меншою кривизною. Тому фокусна відстань лінзи з більшою кривизною буде меншою, ніж тієї, в якої кривизна менша. Лінза, в якої коротша фокусна відстань, дає більше збільшення, ніж довгофокусна лінза. Тому говорять, що вона „оптично сильніша” від другої лінзи. Заломлювальну здатність лінзи характеризує величина, яку називають оптичною силою лінзи. Таким чином, оптична сила більша в тієї лінзи, в якої фокусна відстань менша. Тому величину, обернену фокусній відстані лінзи, називають оптичною силою цієї лінзи.
Позначимо оптичну силу лінзи буквою D. Тоді:
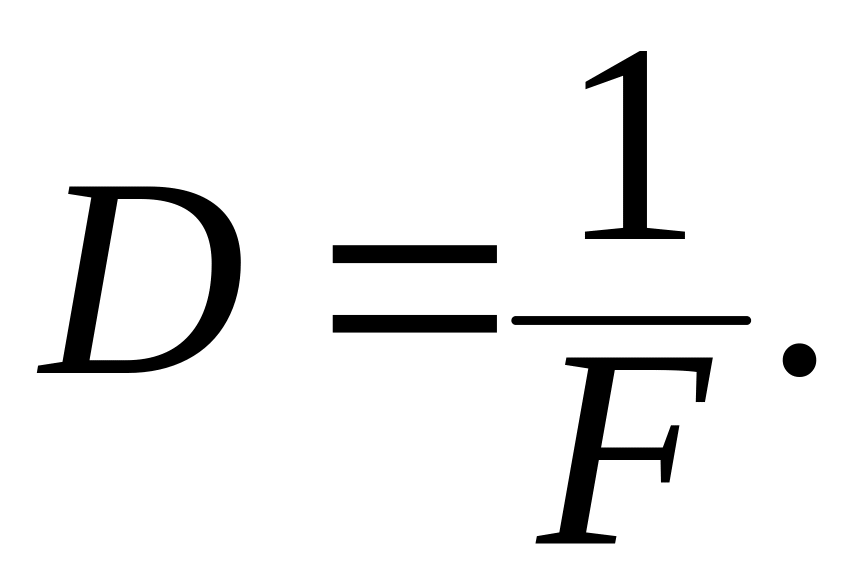
За одиницю оптичної сили взято діоптрію (1 дптр). 1 діоптрія – це оптична сила лінзи, фокусна відстань якої дорівнює 1 м. Отже, при визначенні оптичної сили фокусну відстань слід виражати в метрах.
м-1
.
Оптична сила лінз, фокусна відстань яких менша за 1 м, буде більшою за 1 дптр. Наприклад, оптична сила лінзи з фокусною відстанню 0,25 м дорівнює:
=4
м-1
=4 дптр.
Оптична сила лінзи, фокусна відстань якої більша за 1 м, буде менша 1 дптр. Наприклад, оптична сила лінзи з фокусною відстанню 2,5 м дорівнює:
м
-1
=0,4 дптр.
У розсіювальній лінзі фокус уявний, фокусну відстань вважають від’ємною величиною. Оптична сила розсіювальної лінзи як величина, обернена фокусній відстані, теж буде від’ємною. Оптичну силу збирної лінзи вважають додатною, а оптичну силу розсіювальної лінзи – від’ємною величиною. Наприклад, вираз „оптична сила лінзи дорівнює мінус 2,5 діоптрії” означає, що йдеться про розсіювальну лінзу з фокусною відстанню, яка дорівнює 0,4 м.
5.1.2.Хвильова оптика
5.1.2.1. Інтерференція світла
5.1.2.1.1. Явище інтерференції світла
Інтерференцією називають явище, що виникає при накладанні двох (або більше) хвильових процесів, які мають однакові частоти і напрям коливань, і виражається у перерозподілі енергії хвиль у просторі. Це явище для механічних (пружних) хвиль вже розглянуто в 1.1.8.4, тут же більш детальніше проаналізуємо накладання світлових хвиль, що не є пружними.
Якщо у просторі існують два джерела світлових хвиль, то в кожній точці, куди приходять хвилі від обох джерел, відбувається складання коливань. Відомо, що два гармонічних коливання одного напрямку й однакової частоти,
x1 = A1sin(wt + j1)
та
x2 = A2sin(wt + j2), (5.1.4.)
при складанні дають гармонічне коливання тієї ж частоти w. При цьому амплітуда А результуючого коливання x = x1+x2 зв'язана з амплітудами А1 і А2 коливань, що складаються, співвідношенням:
.
(5.1.5)
Зазначимо, що x1 і x2 у формулі (5.1.4.) може позначати будь-яку фізичну величину, яка змінюється за гармонічним законом при розповсюдженні хвиль (наприклад, для пружних хвиль – механічний зсув частинок середовища). Для світлових явищ маємо справу з гармонічними змінами напруженості електричного та магнітного поля. Енергія гармонічного коливання пропорційна квадрату його амплітуди. Тому на підставі співвідношення (5.1.5.) можна записати:
W
= W1
+ W2
+2
cos(j1
-
j2).
(5.1.6.)
Як бачимо, енергія W результуючого коливання не дорівнює, взагалі кажучи, сумі енергій W1 і W2 коливань, що складаються:
W ¹ W1 + W2 .
З формули (5.1.6.) випливає, що в тих точках простору, де різниця фаз Dj = j1 - j2 хвиль, що туди прийшли, задовольняє умові:
Dj =2kp (k = 0, ± 1, ± 2, …), (5.1.7.)
тобто cosDj =+1, амплітуда і енергія результуючого коливання є максимальними:
;
і
W = Wmax
=
. (5.1.8.)
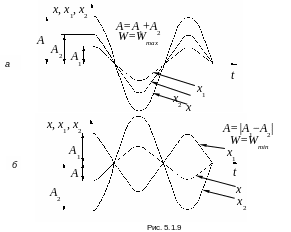
В цих точках хвилі максимально підсилюють одна одну (рис. 5.1.9, а).
У тих точках, де різниця фаз хвиль задовольняє умові:
Dj = (2k + 1)p,
тобто
cosDj = -1,
амплітуда і енергія результуючого коливання є мінімальною:
;
W = Wmin
=
.
(5.1.9)
В цьому випадку хвилі максимально послаблюють одна одну (див.рис. 5.1.9,б).
Зокрема, якщо амплітуди хвиль є однаковими, тобто W1 = W2, то Wmax = 4W1, а Wmin = 0. В цьому випадку хвилі повністю гасять одна одну.