Практичне заняття №4 Тема: Випадкові величини та їх характеристики

9. Дискретні випадкові величини та їх характеристики. Література: [15], розд. ІІІ, §15-17, с. 54-60; §19, с. 62-65.

Випадковою величиною називається змінна величина, яка може приймати ті або інші значення в залежності від різних обставин. Випадкова величина називається дискретною, якщо множина значень її скінчена або зчислена.

Законом розподілу дискретної випадкової величини називається перелік її можливих значень і відповідних їм ймовірностей. Закон розподілу є таблиця:

Значення х	x1	x2	…	xn
Ймовірність р	р1	р2	…	рn

де .

Приклад 4.1 На студентському потоці організовано лотерею, розігруються дві речі по 10 грн. та одна – 30 грн. Скласти закон розподілу суми чистого виграшу для студента, який придбав один квиток за одну грн. Загалом лотерея нараховує 50 квитків.

Розв’язання. Позначимо х – чистий виграш студента, тоді х – шукана величина і може приймати значення – 1 грн., 9 грн., 29 грн. з урахуванням вартості квитка. Отже,

Чистий прибуток	–1	9	29
Ймовірність	0,94	0,04	0,02

де = 0,94 + 0,04 + 0,02 = 1.

Математичним сподіванням дискретної випадкової величини називається сума добутку всіх її значень на відповідні їм ймовірності:

M(x) = x₁p₁ + x₂p₂ + … + x_np_n, (4.1)

де .

Приклад 4.2 У парку організована безпрограшна лотерея. Маємо 1000 виграшів, з них 400 по 50 коп., 300 – по 1 грн., 200 – по 5 грн., 100 – по 10 грн. Знайти середній розмір виграшу для відвідувача парку, що придбав один квиток.

Розв’язання. Середній розмір виграшу дорівнює загальній сумі виграшу, що поділена на загальну кількість виграшів. Тобто:

0,5400 + 1300 + 5200 + 10100 = 2500 грн.

Середній виграш дорівнює 2500/1000 = 2,5.

З іншого боку, якщо розглянемо закон розподілу

хі	0,5	1	5	10
рі	0,4	0,3	0,2	0,1

то таку ж величину отримаємо при знаходженні суми добутку значень випадкових величин на відповідні ймовірності

M(x) = 0,50,4 + 10,3 + 50,2 + 100,1 = 2,5.

Найбільш розповсюджена міра розсіювання – це дисперсія та безпосередньо отримане з неї середнє квадратичне відхилення.

Дисперсія –

ппре

це математичне сподівання квадратів відхилень випадкової величини Х: (х_і – а)² і позначається D(x) або ²(x), тобто

D(x) = M[x – M(x)]²  D(x) = (х_і – а)²p_i, (4.2)

де а – математичне сподівання випадкової величини або

D(x) = M(x²) – M²(x). (4.3)

Середнім квадратичним відхиленням випадкової величини X називається арифметичне значення квадратного кореня від дисперсії, тобто:

(x) = . (4.4)

Нехай дискретна випадкова величина задана законом розподілу. Розглянемо подію, яка полягає в тому, що випадкова величина Y набуде яке-небудь значення менше будь-якого числа X. Ця подія має певну ймовірність.

xi	x1	x2	…	xn
рi	р1	р2	…	рn

Позначимо F(x) = P(y < x).

При зміні X будуть змінюватися і ймовірності. Отже F(x) можна розглядати як функцію змінної величини X.

Функцією розподілу випадкової величини Y називається функція F(x), яка виражає для кожного X ймовірність того, що Y прийме яке-небудь значення менше заданого. F(x) – постійна на інтервалах та має скачки в точках, що відповідають її значенням.

Властивості функції розподілу.

1. Ймовірність того, що випадкова величина Y набуде значення, що належить відрізку [x₁; x₂], дорівнює прирощенню її функції розподілу на цій ділянці, тобто

P(x₁  y  x₂) = F(x₂) – F(x₁). (4.5)

2. Функція розподілу будь-якої випадкової величини є неспадна функція і змінюється від 0 до 1, при зміні x від (–; ), тобто , .

Приклад 4.3 Команда нараховує два стрільців. Кількість балів, що вибиваються кожним з них після одного пострілу, є випадкові величини X та Y, які характеризуються такими законами розподілу:

Число балів xi	3	4	5
P(xi)	0,3	0,4	0,3

Число балів yi	1	2	3	4	5
P(yi)	0,1	0,1	0,1	0,2	0,5

Причому результати пострілів одного з них не впливають на результати іншого.

Потрібно а) скласти закон розподілу числа балів, що вибиваються командою, якщо стрільці роблять по одному пострілу; б) знайти математичне сподівання та дисперсію для команди; в) скласти та побудувати функцію розподілу.

Розв’язання.

1. Складемо таблицю

№	xi	yi	xi + yi	P(xi + yi) = P(xi)P(yi)
1	3	1	4	0,30,1=0,03
2	3	2	5	0,30,1=0,03
3	3	3	6	0,30,1=0,03
4	3	4	7	0,30,2=0,06
5	3	5	8	0,30,5=0,15
6	4	1	5	0,40,1=0,04
7	4	2	6	0,40,1=0,04
8	4	3	7	0,40,1=0,04
9	4	4	8	0,40,2=0,08
10	4	5	9	0,40,5=0,2
11	5	1	6	0,30,1=0,03
12	5	2	7	0,30,1=0,03
13	5	3	8	0,30,1=0,03
14	5	4	9	0,30,2=0,06
15	5	5	10	0,30,5=0,15

Таким чином, закон розподілу числа отриманих балів команди буде:

xi	4	5	6	7	8	9	10
pi	0,03	0,07	0,1	0,13	0,26	0,26	0,15

2. Знаходимо математичне сподівання:

М(х) = = 40,03 + 50,07 + 60,1 + 70,13 + 80,26 + 90,26 + 100,15 = 7,9.

Для знаходження дисперсії скористуємось формулою (4.3). Для чого, спочатку обчислимо математичне сподівання випадкової величини х2 і складемо закон розподілу цієї величини:

х2	16	25	36	49	64	81	100
рі	0,03	0,07	0,1	0,13	0,26	0,26	0,15

Таким чином, отримаємо:

М(х²) = 160,03 + 250,07 + 360,1 + 490,13 + 640,26 + 810,26 + 1000,15 = 64,9.

і оскільки М2(х) = 62,41, то отримаємо дисперсію: D = 64,9 – 62,41 = 2,49.

3. Функцію розподілу знаходимо за визначенням P(x₁  x < x₂) = F(x), тобто,

1. P(–   x < 4) = 0;

2. P(4  x < 5) = 0,03;

3. P(5  x < 6) = 0,03 + 0,07 = 0,1;

4. P(6  x < 7) = 0,1 + 0,1 = 0,2;

5. P(7  x < 8) = 0,2 + 0,13 = 0,33;

6. P(8  x < 9) = 0,33 + 0,26 = 0,59;

7. P(9  x < 10) = 0,59 + 0,26 = 0,85;

8. P(10  x < ) = 0,85 + 0,15 = 1.

Тоді, графік функції розподілу матиме такий вигляд (рис. 1.3):

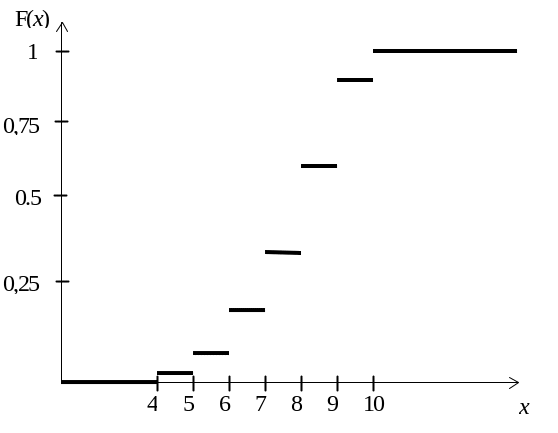
Рис. 1.3 Графік функції розподілу

Приклад 4.4 Вірогідний прогноз для відсоткової зміни вартості акцій по відношенню до їх поточного курсу (величина Х) протягом шести місяців представлений у вигляді закону розподілу

X	5	10	15	20	25	30
pi	0,1	0,1	0,2	0,3	0,2	0,1

Знайти ймовірність того, що покупка акцій буде більш вигідною, ніж розміщення грошей на банківський депозит під 3% на місяць строком на 6 місяців.

Розв’язання. Приріст суми на банківському депозиті за умов 3% на місяць складе через 6 місяців [(1,03)⁶ – 1]100% = 19,4%. Ймовірність того, що покупка акцій вигідніше банківського депозиту, визначається сумою ймовірностей, відповідних більш високому росту курсу акцій: P(X > 19,4) = 0,3 + 0,2 + 0,1 = 0,6.

Приклад 4.5 Нехай щоденні витрати на обслуговування та рекламу автомобілів у автосалоні складають в середньому 120 тис. грош. од., а число продаж автомашин (Х) протягом дня підпорядковане закону розподілу:

X	0	1	2	3	4	5	6	7	8	9
pi	0,25	0,2	0,1	0,1	0,1	0,1	0,05	0,05	0,025	0,025

Знайти математичне сподівання щоденного прибутку при ціні машини у 150 тис. грош. од. та дисперсію щоденної продажі числа автомашин.

Розв’язання. Щоденний прибуток обчислюється за формулою: П = (150Х – 120). Шукана характеристика М(П) знаходиться з використанням властивостей математичного сподівання (тис. грош. од.): М(П) = М(150Х –120)= = 150 М(Х) – 120. Знайдемо за формулою (4.1) значення М(Х) = 00,25 + 10,2 + + 20,1 + 30,1 + 40,1 + 50,1 + 60,05 + 70,05 + 80,025 + 90,025 = 2,675. Таким чином математичне сподівання щоденного прибутку складе: М(П) = 1502,675 – – 120 = 281,25 тис. грош. од.

Дисперсію знайдемо за формулою (4.3) і для цього знайдемо математичне сподівання М(Х²) = 00,25 + 10,2 + 40,1 + 90,1 + 160,1 + 250,1 + 360,05 + + 490,05 + 640,025 + 810,025 = 13,475. Тоді шукана величина дисперсії буде такою: D(X) = 13,475 – 2,675² = 6,319.

Приклад 4.6 Банк видав кредити 1000 різним позичальникам в розмірі 100 тис. грош. од. кожному під ставку позикового відсотка 30%. Знайти математичне сподівання, дисперсію та середньоквадратичне відхилення прибутку банку, якщо ймовірність повернення кредиту позичальником дорівнює p = 0,85.

Розв’язання. Оскільки постачальник між собою не пов’язані, то можна вважати, що маємо 1000 незалежних випробувань. Ймовірність утрати кредиту для банку в кожному випробуванні дорівнює q = 1 – p = 1 – 0,85 = 0,15. Нехай Х – число постачальників, що повернули кредит з позиковими відсотками, тоді прибуток банку визначається за формулою: П=(1+30%/100%)100Х –1000100 = = 130Х – 100 000.

Х є випадковою величиною з біноміальним законом розподілу, тобто ймовірність кожного х_і обчислюється за формулою Бернуллі. У цьому випадку математичне сподівання прибутку, згідно формули (4.1), дорівнює: М(П) = 130  М(Х) – 100 000 = 13010000,85 – 100 000 = 10 500 тис. грош. од.

Використовуючи властивості дисперсії та формули обчислення дисперсії для біноміального закону розподілу випадкової величини, одержимо дисперсію прибутку банку: D(П) = D(130X – 100 000) = 130²10000,850,15 = 2154750 тис. грош. од. За формулою (4.4) обчислюємо середньоквадратичне відхилення прибутку (П) = = 1467,91 тис. грош. од.

Зауваження. Оскільки видача кредиту має зміст тільки при додатному математичному сподіванні прибутку (додатна середня величина прибутку), то позначивши n – кількість позичальників, S – розмір кредиту, r – ставка позикового відсотка, p – ймовірність повернення кредиту позичальником, q – ймовірність втрати кредиту для банку та з умови M(П) > 0 можна записати умову на ставку позикового відсотка r > 100q/p або r > 100(1 – p)/p.

10. Неперервні випадкові величини та їх характеристики. Література: [15], розд. ІІІ, §20-21, с. 66-72.

Випадкова величина – називається неперервною, якщо функція розподілу її скрізь безперервна, а похідна функції безперервна в усіх точках, за винятком зліченного числа точок на будь-якому скінченому інтервалі.

Для безперервної величини, імовірність того, що величина Y набуде значення, що входить в інтервал [x₁; x₂], дорівнює різниці функції розподілу, тобто

P(x₁  Y  x₂) = F(x₂) – F(x₁). (4.6)

Щільністю ймовірності f(x) називається похідна від функції розподілу випадкової величини

f(x) = F (x). (4.7)

Інакше, функцію розподілу можна знайти, якщо відома щільність розподілу за формулою:

. (4.8)

Функція f(x) характеризує щільність, з якою розподіляються значення випадкової величини в даній точці. Інколи f(x) називають диференціальною функцією розподілу, або диференціальним законом розподілу.

Крива, що відображає щільність розподілу випадкової величини, називається кривою розподілу.

Властивості щільності розподілу.

1. Щільність розподілу – невід’ємна функція, тобто геометрично значить, що всі криві вище OX.

2. , (4.9)

отже на усьому інтервалі х  (–;) подія вірогідна.

Теорема. Імовірність того, що безперервна випадкова величина x набуде яке-небудь значення з інтервалу (a, b), рівна визначеному інтегралу:

. (4.10)

Зауваження. Функція розподілу F(x), як і всяка ймовірність, є величина безрозмірна. Розмірність щільності розподілу обернена розмірності випадкової величини.

Математичним сподіванням M(x) безперервної випадкової величини x, щільністю ймовірності якої є функція f(x), називається величина інтегралу:

, (4.11)

а дисперсія , (4.12)

або . (4.13)

Приклад 4.7 Випадкова величина Х підпорядкована закону розподілу з щільністю f(x), причому

Потрібно: а) знайти коефіцієнт а; б) побудувати графік розподілу щільності y = f(x); в) знайти імовірність попадання випадкової величини в інтервал (1,2); г) знайти функцію розподілу F(x).

Розв’язання. а) Оскільки всі значення випадкової величини знаходяться в інтервалі (0; 3), то за формулою (4.9):  a = 2/9.

б) Графік розподілу щільності наведений на рис. 1.4.

в) За визначенням знаходимо шукану ймовірність попадання випадкової величини в зазначений інтервал (4.10):

Рис. 1.4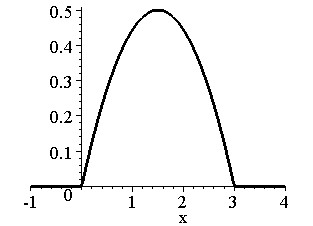

P(1 < x < 2) = .

г) функцію розподілу знаходимо за формулою (4.8): .