Модуль 4 теорія ймовірностей практичне заняття №1 Тема: Класичне визначення ймовірностей

1. Основні поняття теорії ймовірностей. Алгебра подій. Література: [15], розд. ІІІ, §1, с. 29-32.

Події А, В, С утворюють повну групу або повну систему подій, якщо кожна з них є єдино-можливим і несумісним з іншим результатом деякого випробування або явища.

Сумою декількох випадкових подій називається подія, яка полягає у здійсненні хоча б однієї з даних подій, тобто або А, або В, або А і В разом:

А + В = С.

Якщо події А і В несумісні, то сума вказує на те, що відбудеться тільки одна з них.

Добутком подій (перетином) А і В – називається подія С, яка полягає в тому, що обидві події обов’язково відбудуться:

А × В = C.

Приклад 1.1 Два шахісти грають одну партію. Події А – виграє перший гравець; В – виграє другий гравець. Яку подію треба додати, щоб утворилася повна група?

Відповідь: повна група A, , B, , , де – нічийний рахунок, або ; , .

Приклад 1.2 Деяка фірма-постачальник реалізує товар трьом різним фірмам-покупцям. Події A₁, A₂, A₃ – ця фірма-покупець одержує товар у зазначений термін. Як записати події?

1. чи одержить товар хоча б одна фірма в установлений термін?

Відповідь: A₁ + A₂ + A₃ = C (оскільки події сумісні).

2. чи одержать товар усі фірми в установлений термін?

Відповідь: A₁  A₂  A₃ = C.

3. чи одержить товар тільки третя фірма в установлений термін?

Відповідь:   A₃ = C.

4. чи одержить товар тільки одна фірма в установлений термін?

Відповідь: A₁   +  A₂  +   A₃ = C.

2. Елементи комбінаторики. Література: [15], розд. ІІ, §1-4, с. 23-27.

Нехай потрібно виконати послідовно дві дії. Якщо перша дія виконана m різними способами, а друга – n різними способами, то обидві дії можна виконати mn різними способами. Якщо ж потрібно послідовно виконати три дії, причому перша дія може бути виконано m способами, друга – n способами і третя – k способами, тоді три дії можна виконати mnk способами.

Теорема. (Загальне правило множення) Нехай потрібно послідовно виконати n дій, причому перша дія може бути виконана m₁ способами, друга – m₂ способами тощо, нарешті n-а дія – m_n способами. Позначимо S_n – число всіх способів, якими можна виконати n дій. Тоді

S_n = m₁  m₂ …m_n. (1.1)

Приклад 1.3 У забігу брало участь п’ять спортсменів. Скількома способами можна прогнозувати розподіл перших трьох місць, якщо відомо, що ці спортсмени завжди показують різні результати?

Розв’язання. Визначимо скількома способами можуть бути розподілені призові місця для 5 спортсменів:

І місце – 5 способами; ІІ місце – 4 способами; ІІІ місце – 3 способами.

Тоді призові місця можуть бути зайняті 5  4  3 = 60 способами.

Перестановкою з n елементів називається всякий спосіб нумерації цих елементів.

Теорема. Число всіх різних перестановок з n елементів дорівнює n факторіал, тобто n! = 12…n.

Число всіх перестановок з n елементів позначають P_n.

P_n = n! = 12…n. (1.2)

Приклад 1.4 Скільки буквосполучень можна одержати з трьох букв: a, b, c.

Розв’язання. Маємо abc, acb, cab, cba, bac, bca. Тобто P₃ = 3! = 6.

Розміщенням з n елементів по k називається число груп з k елементів, кожна з яких відрізняється порядком елементів або хоча б одним елементом.

Приклад 1.5 Знайти розміщення з трьох елементів по два, тобто з набору a, b, c.

Розв’язання. ab, ba, ac, ca, bc, cb.

Теорема. Число всіх розміщень з n елементів по k обчислюється за формулою

. (1.3)

Приклад 1.6 У студентську раду входить шість студентів. Надійшло розпорядження про преміювання трьох студентів різними сумами. Скількома способами можна це зробити.

Розв’язання. = 6  5  4 = 120 способами.

Сполученням з n елементів по k називається число груп елементів, кожна з яких відрізняється одна від одної хоча б одним елементом. У такий спосіб групування елементів порядок елементів не має значення.

Приклад 1.7 Знайти з набору букв a, b, c.

Розв’язання. Маємо ab, ac, bc. .

Теорема. Число всіх сполучень з n елементів по k обчислюється за формулою

. (1.4)

Приклад 1.8 Студенти однієї групи повинні здати п’ять іспитів протягом 15 днів. Скількома способами можна скласти розклад іспитів, якщо в один день можна здавати тільки один іспит?

Розв’язання. Оскільки порядок іспитів не має значення, то з (1.4) одержимо: .

Приклад 1.9 На річних зборах акціонерів 25 учасників претендують на пости голови, секретаря, скарбника і чотири інших поста в правлінні.

1. Скільки існує способів заміщення трьох перших вакантних місць?

2. Скільки способів заміщення чотирьох вакансій після обрання голови, секретаря, скарбника?

Розв’язання.

1. Для заняття поста голови 25 можливих способів, а для секретаря залишається 24, тоді для скарбника – 23 способи. Отже число усіх способів, якими можна виконати 3 дії будуть за теоремою множення: S₃ = 252423 = 13800.

2. Після обрання голови, секретаря і скарбника залишається 22 учасника. З них 4 поста в правлінні можуть бути зайняті кількістю способів, які обчислені за допомогою сполучення, тобто з (1.4) одержимо = 7315.

Приклад 1.10 У транспортній компанії працює 12 водіїв. Кожний другий день необхідно направити двох водіїв на кожен з п’яти заводів. Скількома способами можна направити водіїв на ці заводи?

Розв’язання. Необхідно виконати послідовно п’ять дій. Перша дія – з 12 водіїв відібрати двох. Це можливо зробити способами. Друга дія – з 10 водіїв, що залишилися, відібрати двох. Це буде способи. Для третьої дії буде способів. Аналогічно для четвертої і п’ятої дії маємо і способів. Отже за теоремою множення, загальна кількість способів буде:

.

3. Класичне визначення ймовірності. Література: [15], розд. ІІІ, §2, с. 32-34.

Число, яке є мірою об’єктивної можливості здійснювання події називається його ймовірністю. Ймовірність події позначають P(A). Відношення числа сприятливих випадків настання події A до числа можливих випадків називається ймовірністю події A

. (1.5)

де m – число випробувань, в яких подія A наступила;

n – загальне число випробувань.

Відношення числа m настання даної випадкової події A до даної серії випробувань n називається частотою або частістю появи події A

. (1.6)

Ймовірність будь-якої події не може бути від’ємною або більше одиниці, отже 0  Р(А)  1, причому P(A) = 0, якщо подія A – неможлива, а P(A) = 1 якщо A – вірогідна подія.

Приклад 1.11 З 60 питань, що входять до екзаменаційних білетів, студент підготував 50 питань. Яка ймовірність того, що два питання з білета студент знає, якщо в білет входить два питання.

Рис. 1.1

Розв’язання. Загальне число можливих випадків – , а студент знає тільки 50 питань, отже число сприятливих випадків буде , тоді шукана ймовірність з (1.5) буде такою .

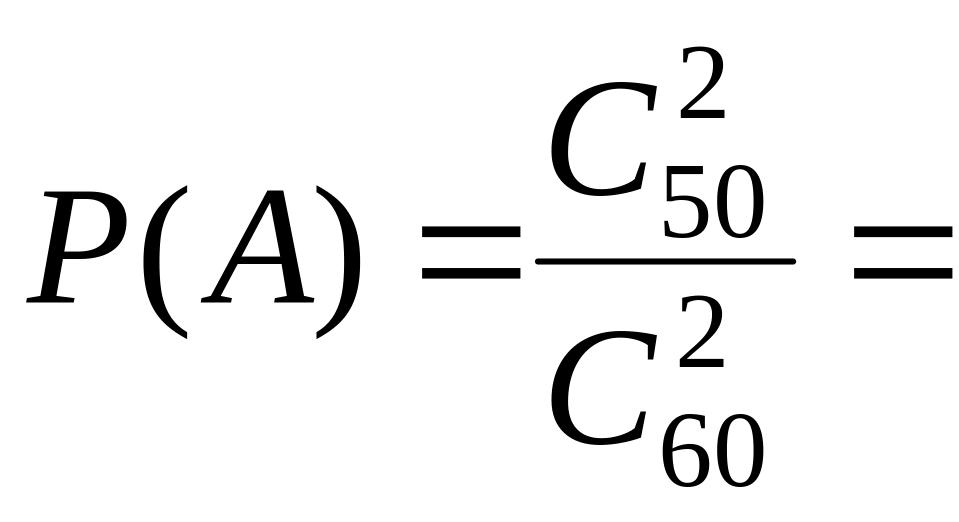
Приклад 1.12 Монету кинуто два рази. Знайти ймовірність того, що хоча б один раз з’явиться герб.

Розв’язання. Побудуємо дерево ймовірностей (рис. 1.1). Нехай г – випав герб, а ц – цифра. Отже, загальна кількість можливих випадків n = 4. Хоча б один раз герб з’являється у трьох подіях, тобто m = 3. Тоді отримаємо Р(А) = 3/4.

Приклад 1.13 На станції відправлення є вісім замовлень на відправлення товарів: п’ять замовлень у межах країни і три на експорт. Яка ймовірність того, що два взяті навмання: 1) внутрішні замовлення; 2) одне замовлення у межах країни й одне на експорт; 3) два замовлення на експорт?

Розв’язання. Для кожного питання знайдемо числа усіх можливих та сприятливих появі даних подій:

1) ; , тоді ;

2) ; , тоді ;

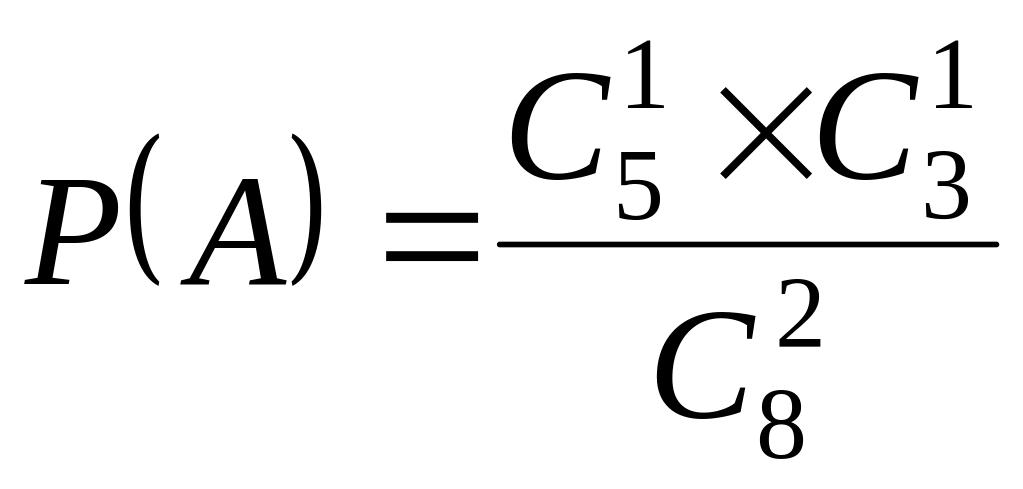3) ; , тоді .

Зауваження. Правильність отриманого розв’язку можна перевірити так: сума верхніх (нижніх) індексів чисельника повинна дорівнювати верхньому (нижньому) індексу знаменника (див. випадок 2)). Особливо це стосується верхніх індексів, оскільки при виборі нуль об’єктів число сполучень буде дорівнювати одиниці (див. випадки 1 або 3).

Приклад 1.14 З партії, що складається з 30 виробів, серед яких п’ять нестандартних, для контролю вибирається 10 виробів. Знайти імовірність того, що всі 10 виробів будуть стандартними.

Розв’язання. Число усіх подій, тобто кількість відібраних будь-яких 10 виробів з 30 дорівнює: . Число сприятливих подій, тобто усі 10 повинні бути стандартними буде , де кількість стандартних визначається за умовою задачі 30 – 5 = 25. Таким чином, шукана ймовірність буде: .

Приклад 1.15 У магазині 10 продавців. З них 6 жінок і 4 чоловіки. У зміну зайняті 3 продавця. Знайти імовірність того, що у випадково обрану зміну вийдуть двоє чоловіків і одна жінка.

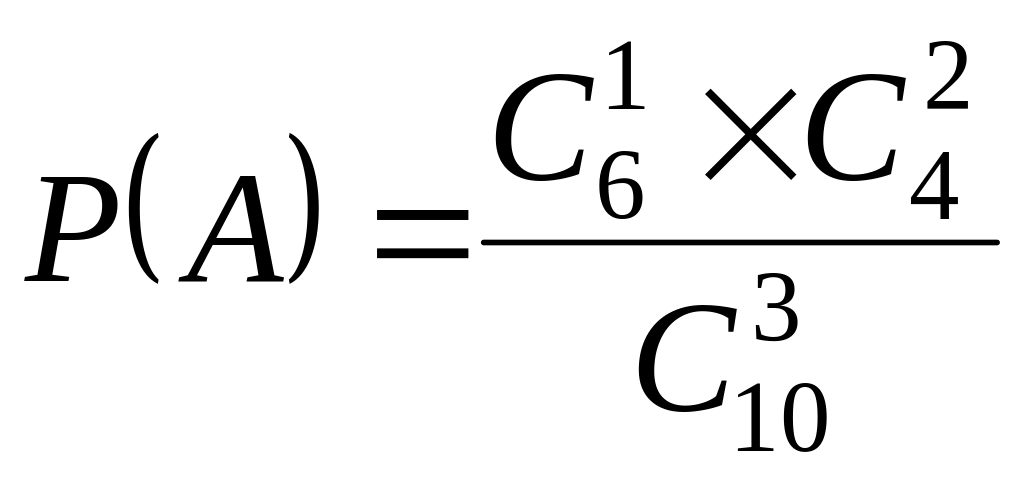Розв’язання. Кількість людей, відібраних будь-яким чином в одну зміну виражається так: . Жінок в цій зміні повинно бути одна з шести, тобто , а чоловіків – два з чотирьох, тобто . При цьому число сприятливих подій буде . Таким чином, ймовірність цієї події буде дорівнювати . Перевіряємо суми верхніх та нижніх індексів: 1+2=3 та 6+4=10.