3.2. Метод наименьших квадратов

Для статистической проверки взаимосвязи между х и у необходимо найти значения коэффициентов а и в, а также случайную компоненту ε_i (линейная модель – y_i=a+bx_i+ε_i). Метод оценки этих коэффициентов должен давать «хорошие» оценки. Чаще других для этого используют метод наименьших квадратов, который дает наилучшие несмещенные оценки. Он называется так, потому что при расчете параметров стараются найти линию минимизирующую сумму квадратов отклонений (значений ошибок, расхождения между фактическими и расчетными значениями у (зависимая переменная)). На графике нанесены наблюдения х_i, у_i (любая точка). Комментируя график, можно сделать вывод:

1. Точки не лежат на одной прямой, можно лишь провести некоторую линию в непосредственной близости от всех точек

2. Можно сделать допущение, что х и у связаны линейной зависимостью.

у

х х

х х

х х

х х

х х

х х

х х

х

х

То есть, можно построить некоторую прямую отражающую зависимость между х_i и у_i,

х_i и у_i – экономические (фактические) переменные,

ŷ- теоретические или расчетные значения зависимой переменной,

и – оценочные значения коэффициентов а и в.

Для того чтобы теоретическая прямая лежала в непосредственной близости от всех точек, то есть от фактических значений у_i, необходимо минимизировать сумму квадратов отклонений между практическими и расчетными значениями.

Продифференцировав данное уравнение по и , получим систему уравнений:

Получаем

Р аскрыв скобки, получаем стандартную форму нормальных уравнений:

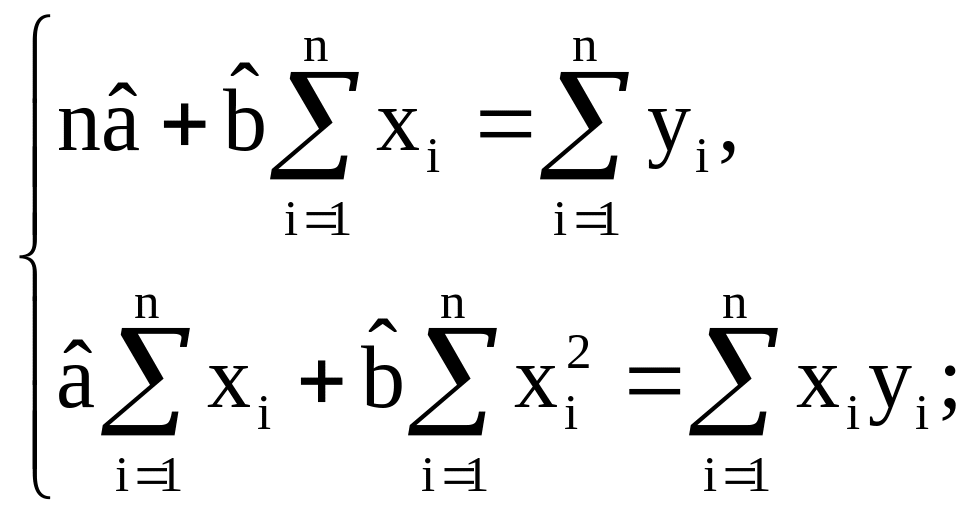
Из этой системы находится оценочное значение коэффициентов а и в, т.е. и :

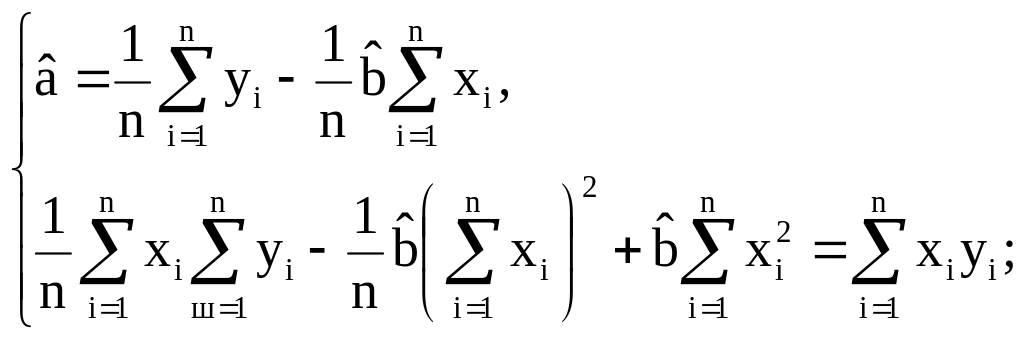
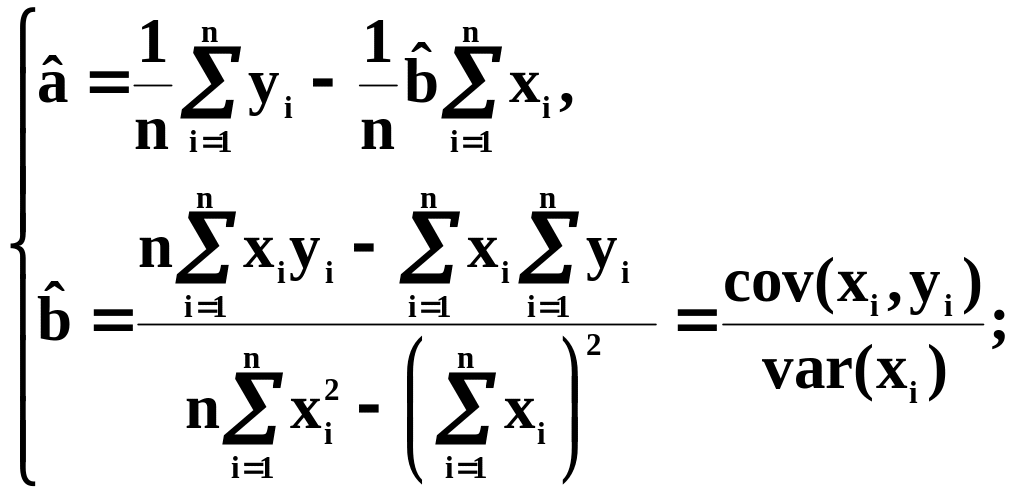
Случайная компонента ε_i находится как разница между фактическим у_i и расчетным значениями : .

3.3. Проверка адекватности регрессионных уравнений

Адекватность регрессионного уравнения, то есть соответствие его реальному моделируемому процессу, достоверность его параметров осуществляется с нескольких позиций:

1. Анализируются показатели качества подгонки регрессионного уравнения;

2. Проверяются различные гипотезы относительно параметров регрессионного уравнения;

3. Проверяется выполнение условий для получения «хороших» оценок методом наименьших квадратов;

4. Производится содержательный анализ регрессионного уравнения.

3.3.1. Показатели качества подгонки регрессионного уравнения

Отражают соответствие расчетных значений зависимой переменной ŷ с фактическими значениями у. Эти показатели, как правило, основываются на квадрате разности фактических и расчетных значений у:

Один из таких показателей – остаточная дисперсия, для однофакторного регрессионного уравнения записывается в следующем виде:

Глядя на уравнение, понятно, что чем меньше ² (остаточная дисперсия), тем лучше регрессионное уравнение. Но ² является размерной величиной (не учитывает единицы измерения), следовательно, сопоставление регрессионных уравнений, отражающих различные переменные или переменные, измеренные в различных единицах измерения, невозможно. Показателем, на основе которого возможно сопоставление различных регрессионных уравнений является коэффициент детерминации (R²), который вычисляется по формуле:

, где – среднее арифметическое значение у_i по всему ряду.

0‹R²‹1, т.е. принимает значения в интервале [0;1], чем ближе R² к 1, тем лучше качество подгонки, это обстоятельство связано с тем, что R² приближается к 1 при приближении вычитаемой дроби к 0. В свою очередь, вычитаемая дробь приближается к 0, при приближении числителя к 0, т.е. при небольших отклонениях фактических и расчетных значений зависимой переменной (ЗП).

На практике, помимо R², часто используют коэффициент корреляции, показывающий степень связи между двумя переменными. Этот показатель не зависит от единицы измерения.

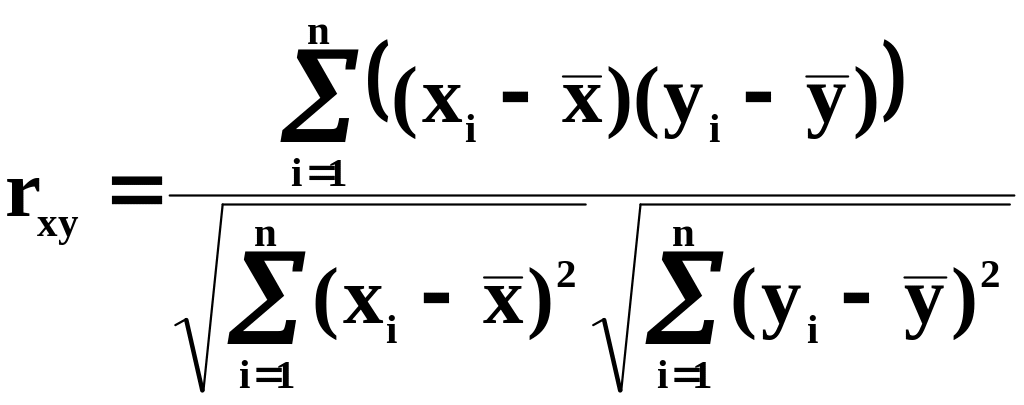
Он показывает силу и направление линейной связи между переменными. Значение коэффициента корреляции находится в промежутке от –1 (в случае отрицательной связи) до +1 (в случае положительной связи)

Если коэффициент корреляции равен 0, то переменные независимы между собой.

Коэффициент корреляции показывает меру статистической связи. По нему нельзя сделать вывод о причинности, т.е. невозможно предположить, что изменение переменной х приводит к изменению переменной у. Следовательно, коэффициент корреляции используется в регрессионном уравнении справочно.

Коэффициенты регрессии (в рассматриваемом случае это коэффициент b) нельзя использовать для непосредственной оценки влияния факторов на результативный признак из-за различия единиц измерения исследуемых показателей. Для этих целей вычисляются коэффициенты эластичности и бета-коэффициент.

Коэффициент эластичности для рассматриваемой модели парной регрессии рассчитывается по формуле:

[%]

Он показывает, на сколько процентов изменяется результативный признак у при изменении факторного признака х на один процент.

Бета-коэффициент в нашем случае задается формулой:

, где – средние квадратические ошибки выборки величин х и у соответственно.

,

Бета-коэффициент показывает, на какую часть величины своего среднего квадратического отклонения изменится в среднем значение результативного признака (y) при изменении факторного признака (x) на величину его среднеквадратического отклонения .